python/TangDou/Topic/【换根】dfs专题.md

树的重心

C. Link Cut Centroids

账号：10402852@qq.com 密码：m****2 关键词：求树的重心

题目大意 给你一棵树的结点数n和n-1条边，你可以删除一条边再增加一条边，使得树的重心唯一,输出这条边

注意：有Specail Judge，如果删除哪条都行，那就随意删除一条就行

性质： ① 删除重心后所得的所有子树，节点数不超过原树的1/2，一棵树最多有两个重心 ② 树中所有节点到重心的距离之和最小，如果有两个重心，那么他们距离之和相等 ③ 两个树通过一条边合并，新的重心在原树两个重心的路径上 ④ 树删除或添加一个叶子节点，重心最多只移动一条边 ⑤ 一棵树最多有两个重心，且相邻

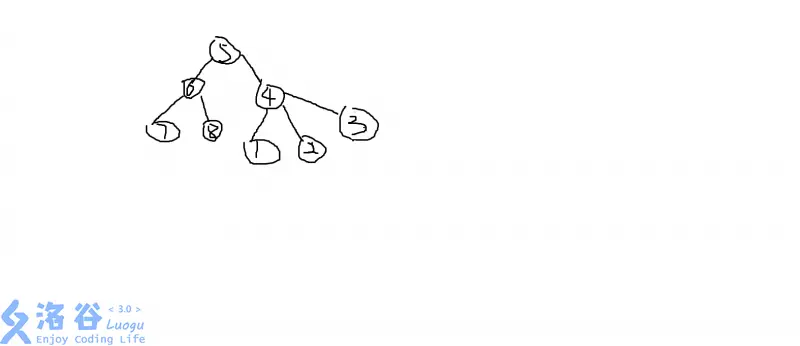
树的重心定义为树的某个节点，当去掉该节点后，树的各个连通分量中，节点数最多的连通分量其节点数达到最小值。树可能存在多个重心。如下图,当去掉点1后，树将分成两个连通块：(2,4,5)，(3,6,7)，则最大的连通块包含节点个数为3。若去掉点2，则树将分成3个部分，(4)，(5)，(1,3,6,7)最大的连通块包含4个节点；第一种方法可以 得到更小的最大联通分量。可以发现，其他方案不可能得到比3更小的值了。所以，点1是树的重心。

思路

• 如果找到只有一个重心，那么直接删一个重心的直连边然后加回去就好
• 如果找到两个重心，那么在其中一个重心上找到一个直连点不是另一个重心，删除连另外一个就好

如何求树的重心？

1、先任选一个结点作为根节点(比如1号节点)，把无根树变成有根树。然后设sz[i]表示以i为根节点的子树节点个数。转移方程为\displaystyle sz[u]=\sum_{fa[v]=u} (sz[v])

2、设son[i]表示删去节点i后剩下的连通分量中最大子树节点个数。其中一部分在原来i其为根的子树。\displaystyle son[i]=max(son[i],sz[j])

解释：j的含义是i的所有儿子节点

另外一部分在i的 上方 子树有n-sz[i]个。

son[i]=max(son[i],n-sz[i])

3、利用重心性质： ① 树必须存在1或2个重心 , ② 如果某个点是重心，那么把它拿下后，其它连通块的个数都需要小于等于整棵树节点个数的一半。 满足条件 ② 的结点数量不会超过2个！分别记录为r_1,r_2。

#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10, M = N << 1;
#define int long long
#define endl "\n"

// 链式前向星
int e[M], h[N], idx, w[M], ne[M];
void add(int a, int b, int c = 0) {
    e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx++;
}

int sz[N];  // sz[i]:以i为根的子树中节点个数
int son[N]; // son[i]:去掉节点i后，剩下的连通分量中最大子树节点个数
int r1, r2, n;

void dfs(int u, int fa) {
    sz[u] = 1;  // u为根的子树中，最起码有一个节点u
    son[u] = 0; // 把节点u去掉后，剩下的连通分量中最大子树节点个数现在还不知道，预求最大，先设最小

    for (int i = h[u]; ~i; i = ne[i]) { // 枚举u的每一条出边
        int v = e[i];
        if (v == fa) continue;
        dfs(v, u);                   // 先把v为根的子树遍历完
        sz[u] += sz[v];              // 把 v中获取填充的sz[v]值，用于组装自己sz[u]
        son[u] = max(son[u], sz[v]); // 如果把u节点去掉，那么它的所有子节点v为根的子树中节点数，可以参加评选：
        // 评选的标准是：son[i]:去掉节点i后，剩下的连通分量中最大子树节点个数
    }
    son[u] = max(son[u], n - sz[u]);         // 右上角的那一块也可能成为评选的获胜者
    if ((son[u] << 1) <= n) r2 = r1, r1 = u; // 删除重心后所得的所有子树，节点数不超过原树的1/2，一棵树最多有两个重心
    // 如果模拟u被删除后，得到的所有子树中节点数量最多的没有超过原树的1/2,那么这个r1=u表示：找到了一个重心u
    // r2=r1表示：如果找到两个重心，那么r1,r2 一人一个，此时，r1中肯定有值，但 r2不一定有值
}

signed main() {
    int T;
    cin >> T;
    while (T--) {
        cin >> n;
        // 多组测试数据，清空
        memset(sz, 0, sizeof sz);
        memset(son, 0, sizeof son);
        // 初始化链式前向星
        memset(h, -1, sizeof h);
        idx = 0;

        r1 = r2 = 0;                  // 重心清零
        for (int i = 1; i < n; i++) { // n-1条边
            int x, y;
            cin >> x >> y;
            add(x, y), add(y, x);
        }
        dfs(1, 0); // 以1号点为入口，它的父节点是0

        if (r2 == 0) { // 如果只有一个重心，r2=0表示没有第二个重心
            int u = r1, v = e[h[u]];
            cout << u << " " << v << endl; // 切掉一条边u->v
            cout << u << " " << v << endl; // 加一条边 u->v
        } else {                           // 如果有两个重心
            int u = r2, v;
            for (int i = h[u]; ~i; i = ne[i]) { // 不要删除掉两个重心相连接的那条边
                v = e[i];
                if (v != r1) break; // 只要对方节点不是另一个重心，那么就是可以删除的
            }
            cout << u << " " << v << endl;  // 切一条边u->v，第二个重心所在边需要被切掉
            cout << v << " " << r1 << endl; // 加一条边v->r1,不走u了，走了u的一个子节点v
        }
    }
    return 0;
} 

树的直径

AcWing 1072 树的最长路径

Code

#include <bits/stdc++.h>

using namespace std;
const int N = 10010, M = N << 1;
int n; // n个结点

// 链式前向星
int h[N], e[M], w[M], ne[M], idx;
void add(int a, int b, int c) {
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++;
}

// 换根dp模板
int ans;          // 答案,直径
int d1[N], d2[N]; // d1[i],d2[i]:经过i点的最长,次长长度是多少
bool st[N];       // 是不是遍历过了
void dfs(int u) {
    st[u] = true;
    for (int i = h[u]; ~i; i = ne[i]) {
        int v = e[i];
        if (st[v]) continue; // v点访问过了

        // 走v子树,完成后，v子树中每个节点的d1[v],d2[v]都已经准备好，u节点可以直接利用
        dfs(v);

        // w[i]:u->v的路径长度,d1[u]:最长路径,d2[u]:次长路径
        if (d1[v] + w[i] >= d1[u])               // v可以用来更新u的最大值
            d2[u] = d1[u], d1[u] = d1[v] + w[i]; // 最长路转移
        else if (d1[v] + w[i] > d2[u])
            d2[u] = d1[v] + w[i]; // 次长路转移
    }
    // 更新结果
    ans = max(ans, d1[u] + d2[u]);
}

int main() {
    cin >> n;
    memset(h, -1, sizeof h);      // 初始化邻接表
    for (int i = 1; i < n; i++) { // n-1条边
        int a, b, c;
        cin >> a >> b >> c;
        add(a, b, c), add(b, a, c); // 换根dp一般用于无向图
    }
    dfs(1); // 任选一个点作为根节点,此处选择的是肯定存在的1号结点
    cout << ans << endl;
    return 0;
}

换根DP

换根DP，又叫二次扫描，是树形DP的一种。

其相比于一般的树形DP具有以下特点：

• ① 以树上的不同点作为根，其解不同
• ② 故为求解答案，不能单求某点的信息，需要求解每个节点的信息
• ③ 故无法通过一次搜索完成答案的求解，因为一次搜索只能得到一个节点的答案 难度也就要比一般的树形DP高一点。

题单

P3478 STA-Station

题意：给定一个n个点的无根树，问以树上哪个节点为根时，其所有节点的深度和最大？ 深度：节点到根的简单路径上边的数量 关键词：换根DP模板题

如果我们假设某个节点为根，将无根树化为有根树，在搜索回溯时统计子树的深度和，则可以用一次搜索算出以该节点为根时的深度和，其时间复杂度为 O(N)。

但这样求解出的答案只是以该节点为根的，并不是最优解。

如果要暴力求解出最优解，则我们可以枚举所有的节点为根，然后分别跑一次搜索，这样的时间复杂度会达到O(N^2)，显然不可接受。

所以我们考虑在第二次搜索时就完成所有节点答案的统计——

• ① 我们假设第一次搜索时的根节点为1号节点，则此时只有1号节点的答案是已知的。同时第一次搜索可以统计出所有子树的大小。

• ② 第二次搜索依旧从1号节点出发，若1号节点与节点x相连，则我们考虑能否通过1号节点的答案去推出节点x的答案。

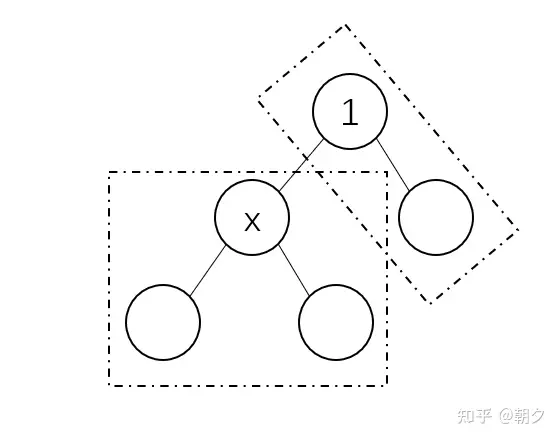
• ③ 我们假设此时将根节点换成节点x，则其子树由两部分构成，第一部分是其原子树，第二部分则是1号节点的其他子树（如下图）。

• ④ 根从1号节点变为节点x的过程中，我们可以发现第一部分的深度降低了1，第二部分的深度则上升了1，而这两部分节点的数量在第一次搜索时就得到了。

故得到递推公式：

f[v]=f[u]-siz[v]+(siz[1]-siz[v]),fa[v]=u

简化一下就是

f[v]=f[u]+siz[1]-2\times siz[v]=f[u]+n-2\times siz[v]

#include <bits/stdc++.h>
using namespace std;
const int N = 1000010, M = N << 1;
#define int long long
#define endl "\n"

// 链式前向星
int e[M], h[N], idx, w[M], ne[M];
void add(int a, int b, int c = 0) {
    e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx++;
}

int n; // n个节点

int depth[N]; // depth[i]:在以1号节点为根的树中，i号节点的深度是多少
int sz[N];    // sz[i]:以i号节点为根的子树中有多少个节点
int f[N];     // DP结果数组，f[i]记录整个树以i为根时，可以获取到的深度和是多少

// 第一次dfs
void dfs1(int u, int fa) {
    sz[u] = 1;                // 以u为根的子树，最起码有u一个节点
    depth[u] = depth[fa] + 1; // u节点的深度是它父节点深度+1
    for (int i = h[u]; ~i; i = ne[i]) {
        int v = e[i];
        if (v == fa) continue;
        dfs1(v, u);     // 深搜v节点,填充 sz[v],depth[v]
        sz[u] += sz[v]; // 在完成了sz[v]和depth[v]的填充工作后，利用儿子更新父亲的sz[u]+=sz[v];
    }
}

// 第二次dfs
void dfs2(int u, int fa) {
    for (int i = h[u]; ~i; i = ne[i]) {
        int v = e[i];
        if (v == fa) continue;
        f[v] = f[u] + n - 2 * sz[v];
        dfs2(v, u);
    }
}

signed main() {
    memset(h, -1, sizeof h); // 初始化链式前向星

    cin >> n;
    for (int i = 1; i < n; i++) { // n-1条边
        int a, b;
        cin >> a >> b;
        add(a, b), add(b, a); // 换根DP，无向图
    }

    // 1、第一次dfs,以1号节点为根，它的父节点不存在，传入0
    dfs1(1, 0);

    // 2、换根
    for (int i = 1; i <= n; i++) f[1] += depth[i]; // DP初始化，以1号节点为根时，所有节点的深度和
    dfs2(1, 0);                                    // 从1号节点开始，深度进行换根

    // 3、找答案
    int ans = 0, id = 0;
    for (int i = 1; i <= n; i++)            // 遍历每个节点
        if (ans < f[i]) ans = f[i], id = i; // ans记录最大的深度值，id记录以哪个节点为根时取得最大值
    // 输出以哪个节点为根时，深度和最大
    cout << id << endl;
}

总结与进阶

由此我们可以看出换根DP的套路：

• 指定某个节点为根节点。
• 第一次搜索完成预处理（如子树大小等），同时得到该节点的解。
• 第二次搜索进行换根的动态规划，由已知解的节点推出相连节点的解。

P1364 医院设置

一、O(N^3)算法

#include <bits/stdc++.h>
using namespace std;
const int N = 1000010;
const int INF = 0x3f3f3f3f;

int g[150][150];
int w[N];

int main() {
    int n;
    cin >> n;

    // 地图初始化
    memset(g, 0x3f, sizeof g);
    for (int i = 1; i <= n; i++) g[i][i] = 0;

    for (int i = 1; i <= n; i++) {
        int a, b;
        cin >> w[i] >> a >> b;
        g[i][a] = g[a][i] = 1; // 左链接，右链接，二叉树，和一般的不一样
        g[i][b] = g[b][i] = 1;
    }

    // floyd
    for (int k = 1; k <= n; k++)
        for (int i = 1; i <= n; i++)
            for (int j = 1; j <= n; j++)
                if (g[i][j] > g[i][k] + g[k][j]) g[i][j] = g[i][k] + g[k][j];

    int ans = INF;
    for (int i = 1; i <= n; i++) {
        int s = 0;
        for (int j = 1; j <= n; j++) s += w[j] * g[i][j];
        ans = min(ans, s);
    }
    printf("%d", ans);
    return 0;
}

二、O(N^2)算法 n 的值很小，最多可以有 O(n^3) 的时间复杂度。

那么就可以枚举每一个节点，计算它的 最小距离和 ，再统计答案。

最小距离和 怎么计算呢？容易想到的是枚举所有节点，算出两个节点之间的距离，再乘上这个节点的价值。

这样就需要求出节点之间的距离。先枚举起点，然后算出每个节点到这个起点间的距离。我用的是一个朴素的 dfs，在搜索的过程中累加距离，每搜索到一个节点，就储存这个节点与起点间的距离。

而累加距离也很容易实现，在从一个节点遍历到下一个节点时，step 增加 1；

代码就很好实现了，时间复杂度也不高，O(n^2)。

#include <bits/stdc++.h>
using namespace std;
const int N = 110, M = N << 1;
const int INF = 0x3f3f3f3f;
int n;
int x[N];      // 点权权值数组
int st[N];     // st 数组存是否遍历过这个节点
int dis[N][N]; // 存节点间的距离

// 链式前向星
int e[M], h[N], idx, w[M], ne[M];
void add(int a, int b, int c = 0) {
    e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx++;
}

void dfs(int root, int u, int step) {         // root 表示根,u:当前走到哪个节点，step:到u点时走了几步
    st[u] = 1;                                // u走过了，防止回头路
    dis[root][u] = step, dis[u][root] = step; // root<->u之间的路径长度

    for (int i = h[u]; ~i; i = ne[i]) {
        int v = e[i];
        if (st[v]) continue;
        dfs(root, v, step + 1);
    }
}

int main() {
    // 初始化链式前向星
    memset(h, -1, sizeof h);

    cin >> n;
    for (int i = 1; i <= n; i++) {
        int a, b;
        cin >> x[i] >> a >> b;
        if (a) add(i, a), add(a, i); // 存图
        if (b) add(i, b), add(b, i);
    }
    for (int i = 1; i <= n; i++) {
        memset(st, 0, sizeof st);
        dfs(i, i, 0); // 搜索
    }
    int ans = INF;
    for (int i = 1; i <= n; i++) {
        int s = 0;
        for (int j = 1; j <= n; j++)
            s = s + x[j] * dis[i][j]; // 累加距离
        ans = min(ans, s);
    }
    cout << ans << endl;
    return 0;
}

三、O(N)算法 如果n=1e6，那么就要考虑换根dp了 我们考虑相邻的医院是否存在转换关系,设其中一个医院为u（父节点），另一个为v(子节点) 如果把u点的医院改为v点，则发现：

如图：以5为根时：

以4为根时：

以v为根的子树的集合的所有人少走1步，但是另一集合的所有人要多走一步

设sz[i]表示以i为根节点的集合人的总数，f[i]表示在i点设置医院的代价，则可转换成：

\large f[v]=f[u]+(sz[1]-sz[v])-sz[v]=f[u]+sz[1]-2\times sz[v]

注： 其中sz[1]表示全部人的数量,一般也写做n

思路： 先算出1个点的代价，之后dp换根直接转换

Code

#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10, M = N << 1;
const int INF = 0x3f3f3f3f;

// 链式前向星
int e[M], h[N], idx, w[M], ne[M];
void add(int a, int b, int c = 0) {
    e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx++;
}
int c[N];
int f[N], sz[N];
int ans = INF;

// 第一次dfs,获取在以1为根的树中:
// 1、每个节点分别有多少个子节点，填充sz[]数组
// 2、获取到f[1],f[1]表示在1点设置医院的代价
// 获取到上面这一组+一个数据，才能进行dfs2进行换根
void dfs1(int u, int fa, int step) {
    sz[u] = c[u]; // 这个挺绝啊~，与一般的统计子树节点个数不同，这里把人数，也就是点权值，也看做是一个节子点，想想也是这个道理
    for (int i = h[u]; ~i; i = ne[i]) {
        int v = e[i];
        if (v == fa) continue;
        dfs1(v, u, step + 1); // 填充深搜v节点为根的子树
        sz[u] += sz[v];       // 在完成了v节点的数据统计后，用v节点的sz[v]结果累加到sz[u]
    }
    f[1] += step * c[u]; // 累加步数*人数 = 1点的总代价,预处理出1点的总代价
}

// 第二次dfs,开始dp换根
void dfs2(int u, int fa) {
    for (int i = h[u]; ~i; i = ne[i]) {
        int v = e[i];
        if (v == fa) continue;
        f[v] = f[u] + sz[1] - sz[v] * 2; // 经典的递推式
        dfs2(v, u);                      // 继续深搜
    }
}

int main() {
    // 初始化链式前向星
    memset(h, -1, sizeof h);

    int n;
    cin >> n;
    for (int i = 1; i <= n; i++) {
        cin >> c[i];
        int a, b;
        cin >> a >> b;
        if (a) add(a, i), add(i, a); // 是一个二叉树结构，与左右节点相链接，但有可能不存在左或右节点，不存在时,a或b为0
        if (b) add(b, i), add(i, b);
    }
    // 1、准备动作
    dfs1(1, 0, 0);
    // 2、换根dp
    dfs2(1, 0);

    // 输出答案
    for (int i = 1; i <= n; i++) ans = min(ans, f[i]);
    cout << ans << endl;
    return 0;
}

P2986 伟大的奶牛聚集

题目描述

Bessie 正在计划一年一度的奶牛大集会，来自全国各地的奶牛将来参加这一次集会。当然，她会选择最方便的地点来举办这次集会。

每个奶牛居住在 N 个农场中的一个，这些农场由 N-1 条道路连接，并且从任意一个农场都能够到达另外一个农场。道路 i 连接农场 A_i 和 B_i，长度为 L_i。集会可以在 N 个农场中的任意一个举行。另外，每个牛棚中居住着 C_i 只奶牛。

在选择集会的地点的时候，Bessie 希望最大化方便的程度（也就是最小化不方便程度）。比如选择第 X 个农场作为集会地点，它的不方便程度是其它牛棚中每只奶牛去参加集会所走的路程之和（比如，农场 i 到达农场 X 的距离是 20，那么总路程就是 C_i\times 20）。帮助 Bessie 找出最方便的地点来举行大集会。

题目分析 这还分析个啥啊，这不就是上一道题的医院选址吗？

Code

#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10, M = N << 1;
#define int long long
#define endl "\n"

// 链式前向星
int e[M], h[N], idx, w[M], ne[M];
void add(int a, int b, int c = 0) {
    e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx++;
}

int c[N]; // 点权数组
int sz[N];  // sz[i]:在以1号节点为根时，i号节点的子节点数量
int dis[N]; // dis[i]:表示i距离起点的长度
int f[N]; // f[i]:把奶牛大集会的地点设为i时的最小代价
int ans = 1e18;

// 第一次dfs,获取在以1为根的树中:
// 1、每个节点分别有多少个子节点，填充sz[]数组
// 2、获取到f[1],f[1]表示在1点设置医院的代价
// 获取到上面这一组+一个数据，才能进行dfs2进行换根
void dfs1(int u, int fa) {
    sz[u] = c[u]; // 这个和医院选址是一样的，点权就是子节点个数
    for (int i = h[u]; ~i; i = ne[i]) {
        int v = e[i];
        if (v == fa) continue;
        dis[v] = dis[u] + w[i]; // 每个点到根节点的距离,这个和医院选址是不一样的，那个是一步+1，用step记录即可，这个还有边权
        dfs1(v, u);             // 深搜
        sz[u] += sz[v];         // 以u为根的子树奶牛数量
    }
    f[1] += dis[u] * c[u]; // 累加 距离*人数=1点的总代价
}

// 第二次dfs,开始dp换根
void dfs2(int u, int fa) {
    for (int i = h[u]; ~i; i = ne[i]) {
        int v = e[i];
        if (v == fa) continue;
        f[v] = f[u] + (sz[1] - sz[v] * 2) * w[i];
        dfs2(v, u);
    }
}
signed main() {
    // 初始化链式前向星
    memset(h, -1, sizeof h);

    int n;
    cin >> n;
    for (int i = 1; i <= n; i++) cin >> c[i];
    for (int i = 1; i < n; i++) {
        int a, b, c;
        cin >> a >> b >> c;
        add(a, b, c), add(b, a, c);
    }
    // 1、准备动作
    dfs1(1, 0);
    // 2、换根dp
    dfs2(1, 0);
    // 输出答案
    for (int i = 1; i <= n; i++) ans = min(ans, f[i]);
    cout << ans << endl;
}

CF1324F.Maximum White Subtree

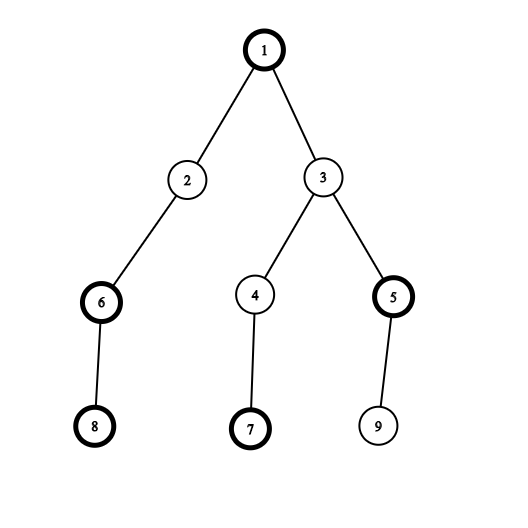
思路分析 这题要求的是求出对任何一个节点v，求出包含这个节点的子树cnt_1−cnt_2的最大值。

暴力想法

首先思考下暴力写法应该如何写。

对于所有可能的路径的贡献值的累加，且贡献值需大于等于0。

• 白的比黑的多，有分, 这时我们选上这棵子树
• 黑的比白的多，没分, 这时我们放弃这棵子树

不妨设f[u]代表u结点的最大值。故

\large f[u]=c[u]+\sum_{v \in son_u}max(0,f[v])

假如用暴力写法，就是对于每个结点u，暴力搜索所有的相邻结点，利用dfs暴力搜索。也就是以每个结点为棵出发，枚举n次dfs,但是结点最大为2∗10^5 这个暴力算法显然会超时，考虑如何优化。

算法优化

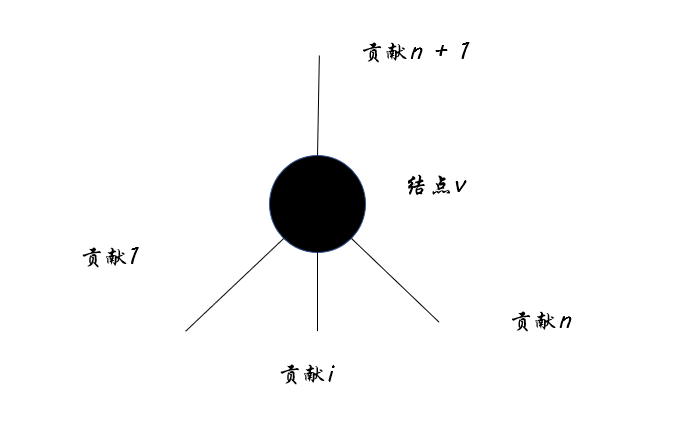
 对于从下往上的贡献，可以利用从下往上的dfs树形dp进行获取,难求的是刨去以v为根的子树的贡献值,也就是向上走的那部分。

设u为节点v的父节点,f[v]代表从下往上以v为根的 白点数减去黑点数 的 最大值,g[v]代表最终的最大值。

根据刨去以v为根的子树的贡献值这个思想，可以发现:

\large add=g[u]−max(0,f[v])

注：fa[v]=u

就是刨去以v为根的子树的贡献值。写出状态转移方程：

\large g[v] = 
 \left\{\begin{matrix}
f[v] &   if \ v = root \\
 f[v]+max(0,g[u]-max(0,f[v]))&  if \ v \neq root
\end{matrix}\right.

因此思路:

• ① 从下往上树形dp,计算f[v]
• ② 从上往下换根dp,计算g[v]

Code

#include <bits/stdc++.h>
using namespace std;
const int N = 2e5 + 10, M = N << 1;

// 链式前向星
int e[M], h[N], idx, w[M], ne[M];
void add(int a, int b, int c = 0) {
    e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx++;
}

int f[N];
int g[N];
int c[N]; // 颜色
int n;    // 节点数量

// 以1号节点为根，跑一遍dfs,填充每个节点的cnt1-cnt2的最大值
void dfs1(int u, int fa) {
    f[u] = c[u]; // 1：白色，-1黑色，正好与 cnt1-cnt2一致,初始值加上了老头子自己的养老钱
    for (int i = h[u]; ~i; i = ne[i]) {
        int v = e[i];
        if (v == fa) continue;
        dfs1(v, u);
        f[u] += max(0, f[v]); // 如果我儿子给我，那我就拿着；如果我儿子不给我钱，或者管我要钱，我就不理它！
    }
}

// 换根dp
void dfs2(int u, int fa) {
    for (int i = h[u]; ~i; i = ne[i]) {
        int v = e[i];
        if (v == fa) continue;
        int val = g[u] - max(f[v], 0);
        g[v] = f[v] + max(val, 0);
        dfs2(v, u);
    }
}

int main() {
    // 初始化链式前向星
    memset(h, -1, sizeof h);
    cin >> n;

    for (int i = 1; i <= n; i++) {
        int x;
        cin >> x;
        c[i] = (x ? x : -1); // 白色c[i]=1，黑色c[i]=-1
    }

    for (int i = 1; i < n; i++) {
        int a, b;
        cin >> a >> b;
        add(a, b), add(b, a);
    }

    // 第一次dfs
    dfs1(1, 0);

    // 它们两个是一个意思
    g[1] = f[1];
    // 换根dp
    dfs2(1, 0);
    // 输出答案
    for (int i = 1; i <= n; i++) printf("%d ", g[i]);
    return 0;
}

P3047 Nearby Cows G

题目大意 题目大意是给你一颗树，对于每一个节点i，求出范围k之内的点权之和。

看数据范围就知道暴力肯定是会TLE飞的，所以我们要考虑如何dp（代码习惯写dfs）

仔细思考一下我们发现点i走k步能到达的点分为以下两种

• 在i的子树中（由i点往下）
• 经过i的父亲（由i点往上）

这样的问题一般可以用两次dfs解决

定义状态:

• f[i][j]表示i点往下j步范围内的点权之和
• g[i][j]表示i点往上和往下走j步范围内点权之和

第一次dfs我们求出所有的f[n][k]，这个比较简单，对于节点u和其儿子v,f[u][k] += f[v][j - 1]就行了。（第一次dfs已知叶子节点推父亲节点）

第二次dfs我们通过已经求出的f数组推g数组，对于u和u的儿子v,

g[v][k] += (g[u][k - 1] - f[v][k - 2])

注意数组下表不要越界。g[i][j]的初始值应该赋为f[i][j]，因为根节点的g[i][j]就是f[i][j]。（第二次dfs已知父亲节点推儿子节点）

P6419 Kamp

https://www.cnblogs.com/Troverld/p/14601347.html

P3647 APIO2014 连珠线

POJ3585 Accumulation Degree

https://blog.csdn.net/qq_34493840/article/details/90575293

CF708C Centroids

https://www.cnblogs.com/DongPD/p/17498336.html

Eg3: AT Educational DP Contest V-Subtree

AcWing 1073. 树的中心

AcWing 1148 秘密的牛奶运输