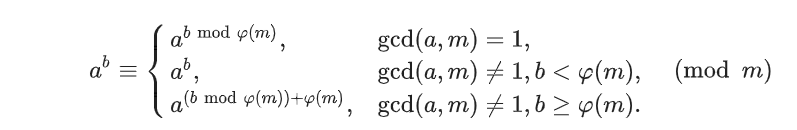4.7 KiB
数论 欧拉降幂+费马小定理+指数循环节+幂塔
### 一、指数循环节
题目大意:求2^a\%1000000007,1 \leq a \leq 10^{100000}。
和队友一直怼 快速幂。然后T了。后来发现这个余数应该是循环的,我当时认为循环节是1000000007。后来才知道发现是1000000006。
让我们来复习一下费马小定理:
\large a^{p-1} \equiv 1 \ (mod \ p) \ gcd(a,p)=1举例子: 取
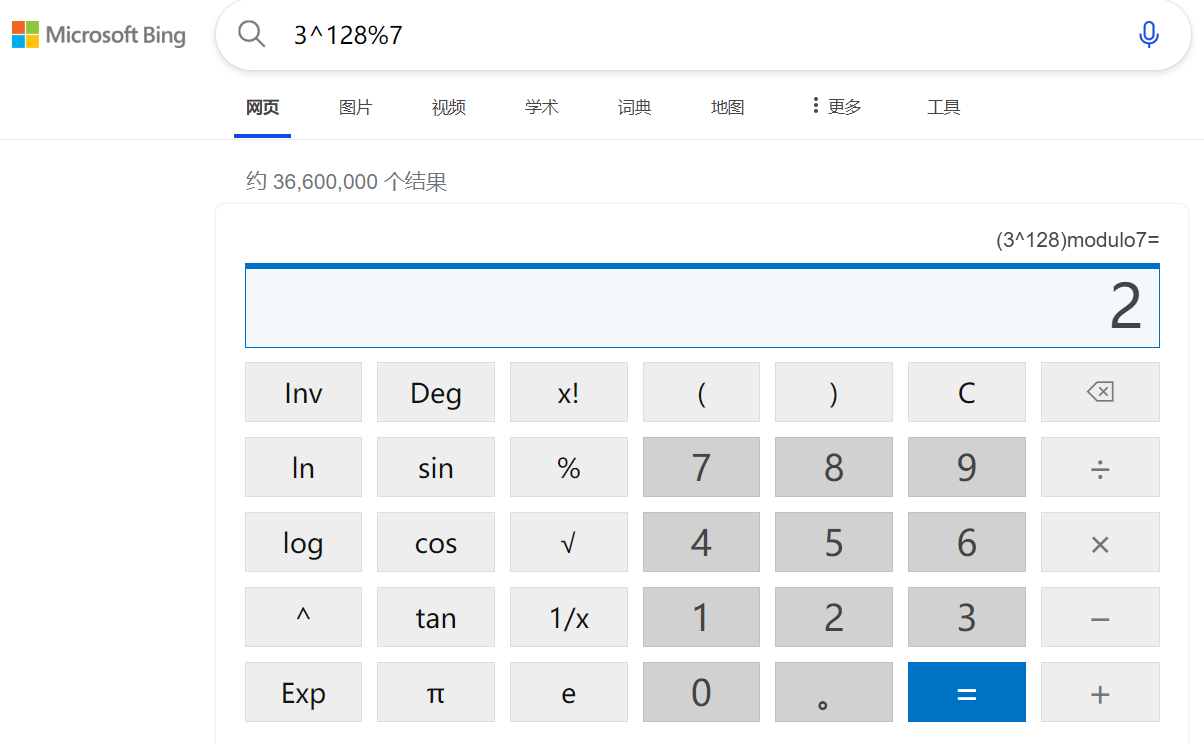
p=7,a=3,gcd(3,7)=1,可以使用费马小定理:3^6 ≡ 1 (mod \ 7)这有啥用呢?比如让我们求3^{128}\%7的值,我们就可以用:3^{128} \%7=3^{21*6+2}\%7=(3^6)^{21}\%7\times 3^2\%7=\underbrace{3^6\%7\times 3^6\%7\times ...\times 3^6\%7}_{\text{21个}}\times 3^2\%7 =\underbrace{1\times 1\times ...\times 1}_{\text{21个}}\times 3^2\%7 =9 \% 7=2验证:我们可以用微软的bing直接输入3^{128}\%7就可以得到答案。
2与1000000007互质,2 ^ 0 = 2 ^ {p-1} 所以循环节为p-1=1000000006。
\therefore 2 ^ a \%1000000007 = 2 ^ {a \%1000000006} \%1000000007。
结果不出我所料:1000000007的欧拉函数就是1000000006。
注:最后这句肯定是废话了,因为
1000000007是质数嘛,\phi(1000000007)当然是1000000006了,这还用说啊~
### 二、幂塔的计算 (欧拉降幂) 形如以下式子的东西叫做 幂塔:
\large a^{a^{a^{a^...}}}题目
给定a,n,m,计算a的n层幂塔对m取模后的结果。
(1<=a,n,m<=1e6)
具体过程:
定义的递归函数形式:f(a,n,m),表示a的n层幂塔对m取模后的结果。
-
首先是对边界情况的判断(递归结束条件)
-
当
m=1时,f(a,n,m)=0.解释:因为任意整数对
1取模都是0,表示任意整数都能被1整除,没有留下余数。 -
当
n<=1时,f(a,n,m)=qmi(a,n,m).解释:
n=1也就是1层,那算就完了
-
-
欧拉降幂公式的
3种情况- 当
gcd(a,m)=1时\large f(a,n,m)=pow(a,f(a,n−1,φ(m)),m)理解:
a^b \equiv a^{b \ mod \ φ(m)},gcd(a,m)=1我们看到:g(a,n)=a^{a^{a^...}}就是n层幂塔,如果把最底下的那个a去掉,剩下的就是n-1层幂塔,即b=g(a,n-1)根据降幂公式,在取模的场景下,b是可以变形为b \mod \ φ(m)即b=f(a,n-1,φ(m))
- 当
-
当
gcd(a,m)\neq 1且a的n−1层幂塔≥ φ(m)时\large f(a,n,m)=pow(a,f(a,n−1,φ(m))+φ(m),m) -
当
gcd(a,m)\neq 1且a的n−1层幂塔< φ(m)时\large f(a,n,m)=pow(a,f(a,n−1,φ(m)),m)
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;
#define int long long
#define endl '\n'
// 快速幂
int qmi(int a, int b, int p) {
int res = 1;
while (b) {
if (b & 1) res = res * a % p;
b >>= 1;
a = a * a % p;
}
return res;
}
// 求单个数的欧拉函数值
int phi(int x) {
int res = x;
for (int i = 2; i <= x / i; i++)
if (x % i == 0) {
res = res / i * (i - 1);
while (x % i == 0) x /= i;
}
if (x > 1) res = res / x * (x - 1);
return res;
}
// 判断n层幂塔指数是否>=phi
bool check(int a, int n, int phi) {
if (n == 0) return phi <= 1; // 0层幂塔是1
if (a >= phi) return true; // 底数a>=phi,那么它的幂塔一定>=phi
return check(a, n - 1, log(phi) / log(a)); // 取对数,消去一层,继续判断
}
// 计算n层幂塔: a^a^a^a..^a (mod m)
// 其中共有n个a
int f(int a, int n, int m) {
if (m == 1) return 0; // 对1取模,恒为0
if (n <= 1) return qmi(a, n, m);
int p = phi(m);
// 互质
if (__gcd(a, m) == 1) return qmi(a, f(a, n - 1, p), m);
// 不互质
if (check(a, n - 1, p))
return qmi(a, f(a, n - 1, p) + p, m); // a的指数>=phi
return qmi(a, f(a, n - 1, p), m); // a的指数<phi, 所以改成对phi取模对答案无影响
}
signed main() {
int T;
cin >> T;
while (T--) {
int a, n, m;
cin >> a >> n >> m;
cout << f(a, n, m) << endl;
}
}