|
|
## 卡特兰数专题($Catalan$)
|
|
|
|
|
|
### 一、什么是卡特兰数?
|
|
|
明安图数,又称卡塔兰数,英文名$Catalan$ $number$,是**组合数学**中一个常出现于各种计数问题中的数列。以中国蒙古族数学家明安图 $(1692-1763)$和比利时的数学家欧仁·查理·卡塔兰 $(1814–1894)$的名字来命名,其前几项为(从第零项开始) : $1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862,16796, 58786 …$
|
|
|
|
|
|
#### 知乎 卡特兰数四连击
|
|
|
https://zhuanlan.zhihu.com/p/31317307
|
|
|
https://zhuanlan.zhihu.com/p/31526354
|
|
|
https://zhuanlan.zhihu.com/p/31585260
|
|
|
https://zhuanlan.zhihu.com/p/31050581
|
|
|
|
|
|
**[嘉持老师的优秀教学视频](https://www.bilibili.com/video/BV1nE411A7ST)**
|
|
|
|
|
|
|
|
|
#### 卡特兰数的几何意义
|
|
|
简单来说,卡特兰数就是一个有规律的数列,在坐标图中可以表示为:从原点$(0,0)$出发,每次向$x$轴或者$y$轴正方向移动$1$个单位,直到到达$(n,n)$点,且在移动过程中不越过第一象限平分线的移动方案总数。
|
|
|
<center><img src='https://img-blog.csdnimg.cn/20210203164401967.png?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L2NoZW5sb25nX2N4eQ==,size_16,color_FFFFFF,t_70'></center>
|
|
|
|
|
|
### 卡特兰数公式推导
|
|
|
我们暂且先不考虑移动过程中不越过第一象限平分线这个约束条件,那么从$(0,0)$点到$(n,n)$点的过程中,我们总共需要向右移动$n$步,向上移动$n$步,一共$2n$步。我们可以理解为在$2n$步里面选出$n$步来向上移动,那么剩下的$n$步就是向右移动的步数,那么方案总数就是$\LARGE \displaystyle C_{2n}^{n}$
|
|
|
|
|
|
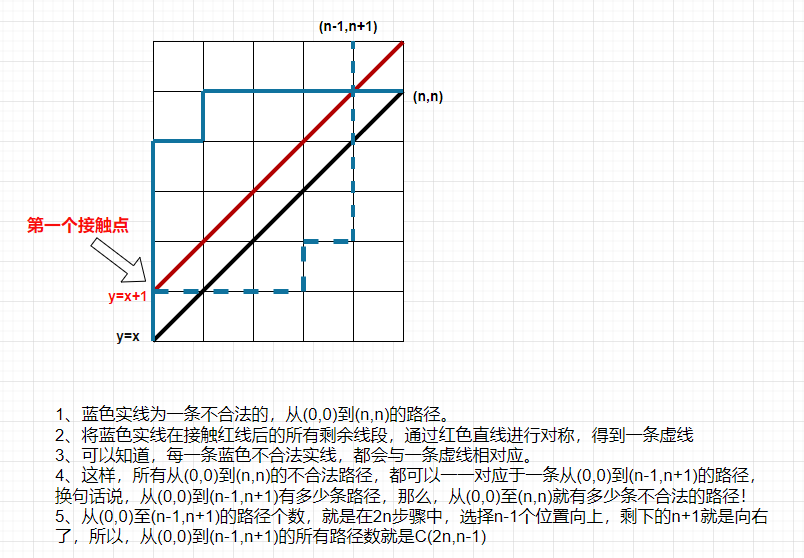
现在,我们来看看如何解决不越过第一象限平分线这个问题。仔细想想,不越过第一象限平分线也就等价于不触碰到$y = x + 1$这条直线。而我们如果把触碰到了直线$y = x + 1$的路线的第一个与$y = x + 1$的触碰点之后的路线关于直线$y = x + 1$对称,并画出对称后的路线
|
|
|
<center><img src='https://img-blog.csdnimg.cn/20210203172545595.png?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L2NoZW5sb25nX2N4eQ==,size_16,color_FFFFFF,t_70'></center>
|
|
|
|
|
|
> <font color='red' size=4><b>黄海解读</b></font>
|
|
|
> 
|
|
|
|
|
|
我们会发现触碰到了直线$y = x + 1$的路径的终点都变成了点$(n-1,n+1)$。也就是说,从$(0,0)$点到$(n,n)$点的路线当中触碰了直线$y = x + 1$的路线条数与从$(0,0)$点到$(n-1,n+1)$点的路线条数的数量是**相等**的。于是从$(0,0)$点到$(n,n)$点的非法路径条数为$\LARGE \displaystyle C_{2n}^{n-1}$ 。
|
|
|
|
|
|
综上所述,从$(0,0)$点到$(n,n)$点满足条件的路径数为
|
|
|
<h2><font color='red'>卡特兰数通项公式I</font></h2></
|
|
|
|
|
|
<font color='red'>$$\huge f(n)=C_{2n}^{n}-C_{2n}^{n-1}$$</font>
|
|
|
|
|
|
---
|
|
|
|
|
|
通过化简,公式可以简化为:
|
|
|
$$\large Catalan_n= C_{2n}^{n}-C_{2n}^{n-1}=\frac{(2n)!}{n! \times n!}-\frac{(2n)!}{(n+1)!\times (n-1)!} \\ =\frac{(2n)!\times (n+1)}{n!\times (n+1)!}-\frac{(2n)!\times n}{n! \times (n+1)!} \\ =\frac{(2n)!\times (n+1)-(2n)!\times n}{n!\times (n+1)!} \\ =\frac{(2n)!}{n!\times (n+1)!}=\frac{1}{n+1}\times \frac{(2n)!}{n!\times n!} =\frac{C_{2n}^n}{n+1}
|
|
|
$$
|
|
|
|
|
|
<h2><font color='red'>卡特兰数通项公式II</font></h2>
|
|
|
|
|
|
<font color='red'>$$\huge \displaystyle f(n)=\frac{C_{2n}^n}{n+1} $$</font>
|
|
|
|
|
|
---
|
|
|
|
|
|
除了这个通项公式之外,卡特兰数还有一个由该通项公式推导而来的递推公式:
|
|
|
|
|
|
$\large \displaystyle Catalan_{n+1}= \frac{1}{n+2}C_{2n+2}^{n+1} \\
|
|
|
=\frac{1}{n+2}\times \frac{(2n+2)!}{(n+1)!\times (n+1)!} \\
|
|
|
=\frac{1}{n+2}\times \frac{(2n)!\times (2n+1) \times (2n+2)}{n! \times n!\times (n+1)^2} \\
|
|
|
=\frac{1}{n+2}\times \frac{(2n+1)\times(2n+2)}{n+1} \times \frac{1}{n+1} \times \frac{(2n)!}{n!\times n!} \\
|
|
|
=\frac{2(2n+1)}{n+2}\times \frac{1}{n+1}\times C_{2n}^n \\
|
|
|
=\frac{4n+2}{n+2}Catalan_n
|
|
|
$
|
|
|
|
|
|
**初始值:`f[0] = f[1] = 1`**
|
|
|
|
|
|
<h2><font color='red'>卡特兰数公式III(递推)</font></h2>
|
|
|
|
|
|
<font color='red'>$$\huge f(n)=\frac{4n-2}{n+1}f(n-1) $$</font>
|
|
|
|
|
|
|
|
|
<h2><font color='red'>卡特兰数公式IV(取模常用)</font></h2>
|
|
|
|
|
|
<font color='red'>$$ \huge f(n)=\frac{(2n)!}{(n+1)! \times n!} $$</font>
|
|
|
|
|
|
|
|
|
|
|
|
<h2><font color='red'>卡特兰数公式V(递推)</font></h2>
|
|
|
<h2><font color='red'>一般不用来实现,用来推规律</font></h2>
|
|
|
|
|
|
<font color='red'>$$\huge \displaystyle f(n)=\sum_{i=0}^{n-1}f(i)f(n-i-1) $$</font>
|
|
|
|
|
|
|
|
|
证明:在$n$对括号的排列中,假设最后一个括号和第$i$个左括号匹配。则在第$i$个左括号之前,一定已经匹配上了($i-1$)对左括号。如下图,因此,此种情况的数量为$f(i-1)*f(n-i)$。($1<=i<=n$)最后一个右括号可以$1\sim n$个左括号匹配共$n$种情况。
|
|
|
|
|
|
<center><img src='https://img-blog.csdnimg.cn/20200410171634180.png?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3dlaXhpbl80NDUyMDg4MQ==,size_16,color_FFFFFF,t_70'></center>
|
|
|
|
|
|
因此,对$i$从$1$到$n$的情况求和得到$\large \displaystyle f(n)=\sum_{i=0}^{n-1}f(i)f(n-i-1)$,即可得到递推公式。
|
|
|
|
|
|
|
|
|
### 二、常见考点
|
|
|
|
|
|
#### 1、 进出栈问题
|
|
|
设栈$S$的初始状态为空,元素$a,b,c,d,e$**依次**入栈,以下**出栈序列**有多少种**可能性**?<font color='red'><b>注意:这个序列顺序是定的.</b></font>
|
|
|
|
|
|
重点:归纳法思考,由大及小。
|
|
|
|
|
|
我们这样去想,假设最终的出栈序列可能性用$f(n)$表示,其中$n$就是元素的个数。
|
|
|
|
|
|
假设第$k$个数是最后出栈的数,那么:
|
|
|
|
|
|
* 比它小的前$k-1$个数,肯定已经完成了入栈,出栈操作。因为从逻辑顺序上来讲,它们无法压到$k$下面去吧。
|
|
|
* 比它大的后$n-k$个数,肯定已经完成了入栈,出栈操作。它们倒是可以压到$k$下面去,但假设$k$是最后一个出栈的,它们不能破坏掉假设,也必须提出出栈。
|
|
|
|
|
|
现在,$k$将原来的问题,划分为两个子问题$f(n-k)$和$f(k-1)$,根据乘法原理,结果就是$f(n-k)*f(k-1)$。
|
|
|
|
|
|
$k$的取值范围是$1 \leq k \leq n$,再根据加法原理:
|
|
|
$$\large f(n)=\sum_{k=1}^{n}f(n-k)\times f(k-1)$$
|
|
|
|
|
|
展开写就是:$$\large f(n)=f(0) \times f(n-1) + f(1) \times f(n-2) + ... +f(n-1)\times f(0)$$
|
|
|
|
|
|
代码实现:
|
|
|
```cpp {.line-numbers}
|
|
|
f[0] = 1;
|
|
|
for (int i = 1; i <= 12; i++) {
|
|
|
int fi = 0;
|
|
|
for (int j = 0; j <= i - 1; j++) fi += f[j] * f[i - j - 1];
|
|
|
cout << fi << " ";
|
|
|
}
|
|
|
```
|
|
|
[P1044 [NOIP2003 普及组] 栈](https://www.luogu.com.cn/problem/P1044)
|
|
|
```cpp {.line-numbers}
|
|
|
#include <bits/stdc++.h>
|
|
|
|
|
|
using namespace std;
|
|
|
typedef long long LL;
|
|
|
const int N = 20;
|
|
|
int f[N];
|
|
|
int main() {
|
|
|
int n;
|
|
|
cin >> n;
|
|
|
f[0] = 1;
|
|
|
for (int i = 1; i <= n; i++)
|
|
|
for (int j = 1; j <= i; j++)
|
|
|
f[i] += f[j - 1] * f[i - j];
|
|
|
cout << f[n] << endl;
|
|
|
return 0;
|
|
|
}
|
|
|
```
|
|
|
|
|
|
#### 2、排队问题
|
|
|
变种(排队问题):出栈入栈问题有许多的变种,比如$n$个人拿$5$元、$n$个人拿$10$元买物品,物品$5$元,老板没零钱。问有几种排队方式。熟悉栈的同学很容易就能把这个问题转换为栈。值得注意的是,由于每个拿$5$元的人排队的次序不是固定的,所以最后求得的答案要$n!$。拿$10$元的人同理,所以还要$n!$。所以这种变种的最后答案为$h(n)*n!$。
|
|
|
[P1754 球迷购票问题](https://www.luogu.com.cn/problem/P1754)
|
|
|
```cpp {.line-numbers}
|
|
|
#include <bits/stdc++.h>
|
|
|
|
|
|
using namespace std;
|
|
|
typedef long long LL;
|
|
|
const int N = 30;
|
|
|
LL f[N];
|
|
|
int main() {
|
|
|
int n;
|
|
|
cin >> n;
|
|
|
f[0] = 1;
|
|
|
for (int i = 1; i <= n; i++)
|
|
|
for (int j = 1; j <= i; j++)
|
|
|
f[i] += f[j - 1] * f[i - j];
|
|
|
cout << f[n] << endl;
|
|
|
return 0;
|
|
|
}
|
|
|
```
|
|
|
#### 3、 二叉树构成问题
|
|
|
有$n$个结点,问总共能构成几种不同的二叉树。
|
|
|
|
|
|
我们可以假设,如果采用中序遍历的话,根结点第$k$个被访问到,则根结点的左子树有$k-1$个点、根结点的右指数有$n-k$个点。$k$的取值范围为$1$到$n$。讲到这里就很明显看得出是卡特兰数了。
|
|
|
|
|
|
[AcWing 1645. 不同的二叉搜索树](https://www.acwing.com/solution/content/35252/)
|
|
|
没有超过$long$ $long$的存储范围的话,可以使用递推;
|
|
|
```cpp {.line-numbers}
|
|
|
#include <bits/stdc++.h>
|
|
|
|
|
|
using namespace std;
|
|
|
typedef long long LL;
|
|
|
const int N = 1010, MOD = 1e9 + 7;
|
|
|
|
|
|
int n;
|
|
|
int f[N];
|
|
|
|
|
|
int main() {
|
|
|
cin >> n;
|
|
|
|
|
|
f[0] = 1;
|
|
|
for (int i = 1; i <= n; i++)
|
|
|
for (int j = 1; j <= i; j++)
|
|
|
f[i] = (f[i] + (LL)f[j - 1] * f[i - j]) % MOD;
|
|
|
|
|
|
cout << f[n] << endl;
|
|
|
return 0;
|
|
|
}
|
|
|
```
|
|
|
|
|
|
[AcWing 1317. 树屋阶梯](https://www.acwing.com/problem/content/description/1319/)
|
|
|
模拟,按照公式(1)进行模拟,需要使用高精度
|
|
|
[黄海的题解](https://www.cnblogs.com/littlehb/p/16365245.html)
|
|
|
|
|
|
|
|
|
[AcWing 1257. 二叉树计数](https://www.acwing.com/problem/content/1259/)
|
|
|
```cpp {.line-numbers}
|
|
|
#include <bits/stdc++.h>
|
|
|
using namespace std;
|
|
|
|
|
|
const int N = 10010; // 5000*2+10
|
|
|
int primes[N], cnt;
|
|
|
bool st[N];
|
|
|
int a[N], b[N];
|
|
|
|
|
|
void get_primes(int n) {
|
|
|
for (int i = 2; i <= n; i++) {
|
|
|
if (!st[i]) primes[cnt++] = i;
|
|
|
for (int j = 0; primes[j] * i <= n; j++) {
|
|
|
st[i * primes[j]] = true;
|
|
|
if (i % primes[j] == 0) break;
|
|
|
}
|
|
|
}
|
|
|
}
|
|
|
|
|
|
int get(int n, int p) { // n!中p的次数
|
|
|
int s = 0;
|
|
|
while (n) n /= p, s += n;
|
|
|
return s;
|
|
|
}
|
|
|
|
|
|
void mul(int a[], int b, int &len) {
|
|
|
int t = 0;
|
|
|
for (int i = 1; i <= len; i++) {
|
|
|
t += a[i] * b;
|
|
|
a[i] = t % 10;
|
|
|
t /= 10;
|
|
|
}
|
|
|
while (t) {
|
|
|
a[++len] = t % 10;
|
|
|
t /= 10;
|
|
|
}
|
|
|
//去前导0
|
|
|
while (len > 1 && !a[len]) len--;
|
|
|
}
|
|
|
|
|
|
int C(int a, int b, int c[]) {
|
|
|
int len = 1;
|
|
|
c[1] = 1;
|
|
|
for (int i = 0; i < cnt; i++) {
|
|
|
int p = primes[i];
|
|
|
int s = get(a, p) - get(b, p) - get(a - b, p);
|
|
|
while (s--) mul(c, p, len);
|
|
|
}
|
|
|
return len;
|
|
|
}
|
|
|
|
|
|
void sub(int a[], int b[], int &len) {
|
|
|
int t = 0;
|
|
|
for (int i = 1; i <= len; i++) {
|
|
|
t = a[i] - b[i] - t;
|
|
|
a[i] = (t + 10) % 10;
|
|
|
t < 0 ? t = 1 : t = 0;
|
|
|
}
|
|
|
while (len > 1 && !a[len]) len--;
|
|
|
}
|
|
|
|
|
|
int main() {
|
|
|
//加快读入
|
|
|
ios::sync_with_stdio(false);
|
|
|
cin.tie(0);
|
|
|
cout.tie(0);
|
|
|
|
|
|
get_primes(N - 10);
|
|
|
|
|
|
int n;
|
|
|
cin >> n;
|
|
|
int a1 = C(n + n, n, a);
|
|
|
int b1 = C(n + n, n - 1, b); // bl下面没有用到,原因是两数相减,我们知道a>b,按着a的长度来就行了
|
|
|
|
|
|
sub(a, b, a1);
|
|
|
|
|
|
for (int i = a1; i >= 1; i--) printf("%d", a[i]);
|
|
|
return 0;
|
|
|
}
|
|
|
```
|
|
|
#### 4、$01$序列
|
|
|
给出一个$n$,要求一个长度为$2n$的$01$序列,使得序列的任意前缀中$1$的个数不少于$0$的个数,有多少个不同的$01$序列?
|
|
|
|
|
|
以下为长度为$6$的序列:
|
|
|
`111000 101100 101010 110010 110100`
|
|
|
|
|
|
类比一下括号问题,此题就是一个祼的卡特兰数问题。
|
|
|
|
|
|
#### 5、$+1$ $-1$序列
|
|
|
$n$个$+1$和$n$个$-1$构成的$2n$项 $a_1,a_2,···,a_{2n}$ ,其部分和满足非负性质,即$a_1+a_2+···+a_k>=0,(k=1,2,···,2n)$ ,有多少个不同的此序列?
|
|
|
|
|
|
此典例解析与$01$序列解析一模一样,即此数列的个数等于第$n$个$Catalan$数,此处就不再赘述。
|
|
|
|
|
|
|
|
|
#### 6、凸多边形划分
|
|
|
在一个$n$边形中,通过不相交于$n$边形内部的对角线,把$n$边形拆分为若干个三角形,问有多少种拆分方案?
|
|
|
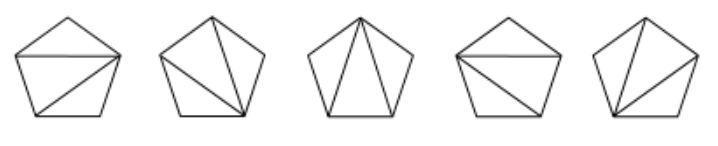
如五边形有如下$5$种拆分方案:
|
|
|
|
|
|
|
|
|
如六边形有如下14种拆分方案:
|
|
|

|
|
|
|
|
|
|
|
|
> **结论**:对凸$n$边形进行不同的三角形分割(只连接顶点对形成$n$个三角形)数为$h[n-2]$
|
|
|
|
|
|
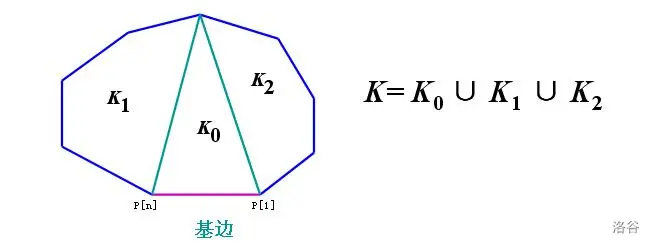
这也是非常经典的一道题。我们可以这样来看,选择一个 **基边** ,显然这是多边形划分完之后某个三角形的一条边。图中我们假设基边是$p_1,p_n$,我们就可以用 $p_1,p_n$ 和另外一个点假设为$p_i$做一个三角形,并将多边形分成三部分(要是$i$与$1,n$挨着的话,就是两部分),除了中间的三角形之外,一边是$i$边形,另一边是$n−i+1$边形。$i$的取值范围是$2$到$n−1$。所以本题的解
|
|
|
$$\large c(n)=c(2)*c(n−1)+c(3)*c(n−2)+...c(n−1)*c(2)$$
|
|
|
|
|
|
令$f(i)=c(i+2)$则
|
|
|
$$\large f(i)=f(0)f(i−1)+f(1)f(i−2)...+f(i−1)f(0)$$
|
|
|
很明显,这就是一个卡特兰数了。
|
|
|
|
|
|
|
|
|
### [四、链接资源](https://blog.csdn.net/Sherry_Yue/article/details/88364746)
|
|
|
|
|
|
|
|
|
### 五、递推与递归的代码实现
|
|
|
```cpp {.line-numbers}
|
|
|
#include <bits/stdc++.h>
|
|
|
|
|
|
using namespace std;
|
|
|
const int N = 10;
|
|
|
|
|
|
|
|
|
int g[N];
|
|
|
|
|
|
// 递归
|
|
|
int f(int n) {
|
|
|
if (n == 0 || n == 1) return 1;
|
|
|
int sum = 0;
|
|
|
// f(0)*f(n-1)+f(1)*f(n-2)+....+f(n-1)*f(0)
|
|
|
for (int i = 0; i < n; i++)
|
|
|
sum += f(i) * f(n - 1 - i);
|
|
|
return sum;
|
|
|
}
|
|
|
int main() {
|
|
|
// 1、递推法
|
|
|
g[0] = g[1] = 1;
|
|
|
for (int i = 2; i < N; i++)
|
|
|
for (int j = 0; j < i; j++)
|
|
|
g[i] += g[j] * g[i - j - 1]; // 考虑思路:画括号法
|
|
|
|
|
|
for (int i = 0; i < N; i++)
|
|
|
cout << g[i] << endl;
|
|
|
|
|
|
// 2 、递归法
|
|
|
for (int i = 0; i < N; i++)
|
|
|
cout << f(i) << endl;
|
|
|
return 0;
|
|
|
}
|
|
|
``` |