python/TangDou/AcWing/BIT/HDU1754.md

##I Hate It

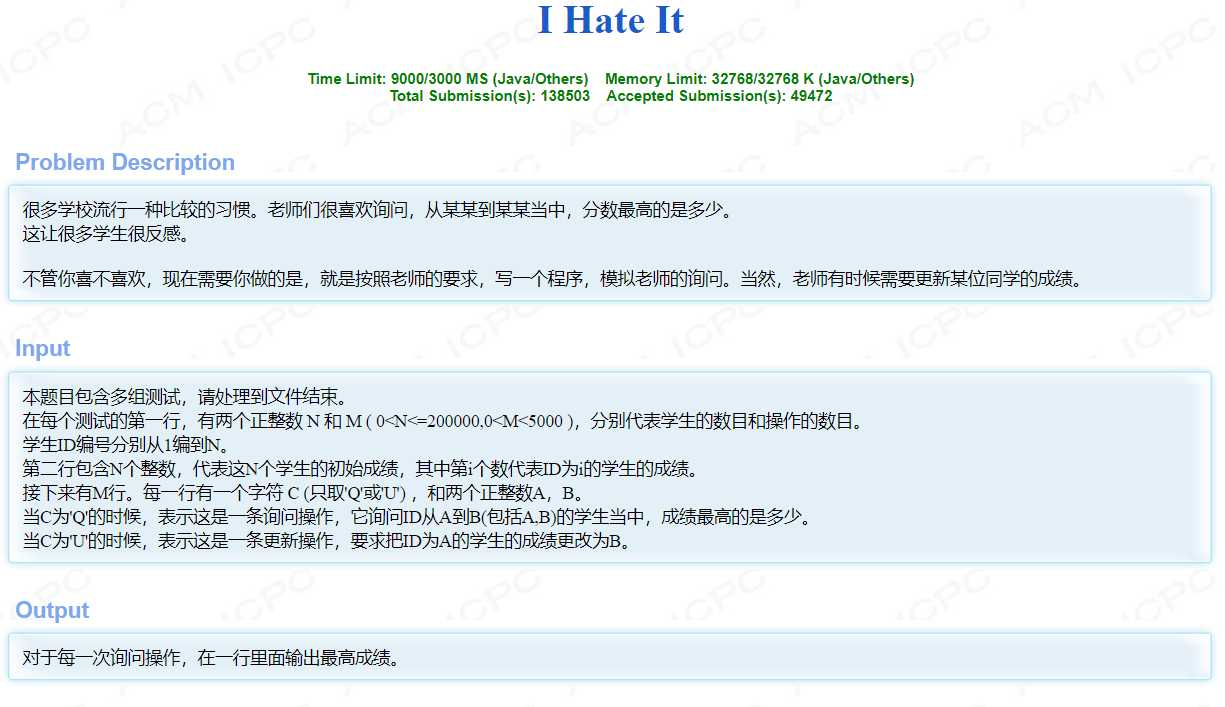
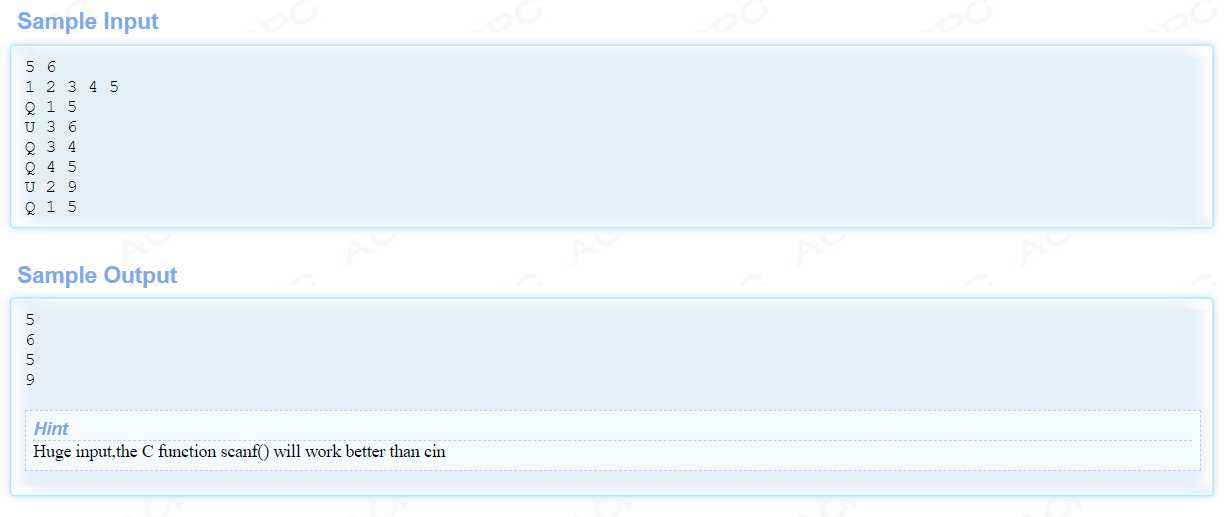
一、题目描述

二、数组的含义

本题是 单点修改，区间求极大极小值 的 模板题

• 在维护和查询区间和的算法中，tr[x]中储存的是[x-lowbit(x)+1,x]中每个数的和

• 在求区间 极值 的算法中，tr[x]储存的是[x-lowbit(x)+1,x]中所有数的 极值

• 求区间极值的算法中还有一个a[i]数组，表示第i个数是多少

三、单点修改引发的变化

数学原理

查询最值

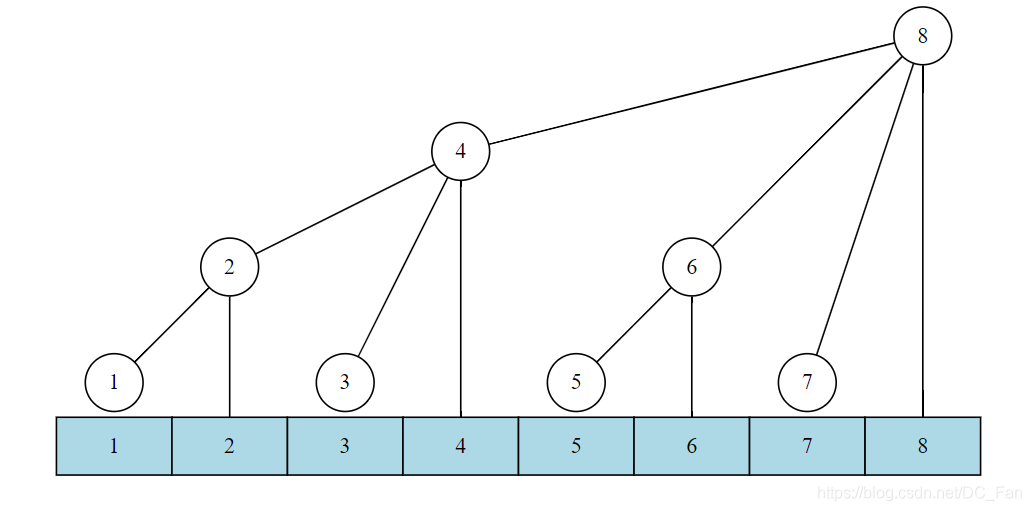
   设 query(x,y) 求区间 [x,y] 之间的最值， 已知 c[x] 表示 [x−lowbit(x)+1,x] 之间的最值，那如何求区间 [x,y] 的最值呢？

我们不难发现:

如果求区间 [1,8] 的最值，就需要点 c[8] 如果求区间 [1,7] 的最值，就需要点 c[7],c[6],c[4] 如果求区间 [2,7] 的最值，就需要点 c[7],c[6],a[4],c[3],a[2] 如果求区间 [2,2] 的最值，就需要点 a[2] 如果求区间 [2,8] 的最值，就需要点 a[8],c[7],c[6],a[4],c[3],a[2]

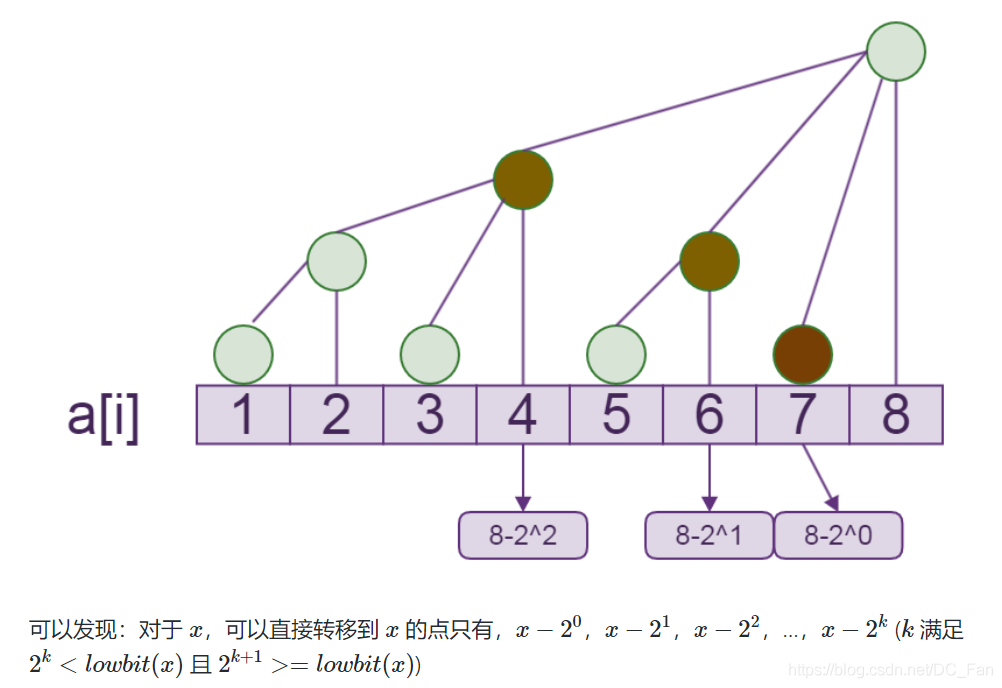
所以，我们发现下面的规律，因为 y−lowbit(y)+1 表示 c[y] 结点所管辖范围的最左边的点

• ① 若 y−lowbit(y)+1>=x, 则query(x,y)=max(c[y],query(x,y−lowbit(y)));
• ② 若 y−lowbit(y)+1<\ \ \ x, 则 query(x,y)=max(a[y],query(x,y−1));
• 边界 x>y

// 对于y来讲，它所管辖的有lowbit(y)个区间。所以对于[x,y]如果y-x>=lowbit(y)，
//  那么tr[y]可以直接拿来用。而如果lowbit(y)超出了[x,y]，那么就y--对x进行逼近
int query(int x, int y) {
    int mx = 0;
    while (x <= y) {
        mx = max(mx, a[y]);
        for (--y; y - x >= lowbit(y); y -= lowbit(y)) mx = max(mx, tr[y]);
    }
    return mx;
}

Code

#include <iostream>
#include <algorithm>
#include <cstdio>
#include <cstring>

using namespace std;
const int N = 200010;

int n, m;     // n个数，m个操作
int a[N];     // 原始数据
char op[110]; // 指令字符串

// 树状数组求最大值模板
int tr[N];
int lowbit(int x) {
    return x & -x;
}
// x这个位置，获得了一个新值c,需要更一下c和它脑袋顶上那些统计数组的信息，也就是最大值或最小值
void update(int x, int c) {
    while (x < N) tr[x] = max(tr[x], c), x += lowbit(x);
}

int query(int x, int y) { // 求x~y之间的最大值
    int mx = 0;
    while (x <= y) {
        mx = max(mx, a[y]);
        // 检查是不是可以完整覆盖掉这个区域，如果是的话，可以PK一下整个完整区域的极值；
        // 否则，就逐步缩小范围继续取小区域中的极值
        for (--y; y - x >= lowbit(y); y -= lowbit(y)) mx = max(mx, tr[y]);
    }
    return mx;
}

/*
答案：
5
6
5
9
*/
int main() {
#ifndef ONLINE_JUDGE
    freopen("HDU1754.in", "r", stdin);
#endif
    // n个数，m个操作
    while (~scanf("%d %d", &n, &m)) {
        memset(tr, 0, sizeof tr);      // 清空树状数组
        for (int i = 1; i <= n; i++) { // 读入n个数
            scanf("%d", &a[i]);
            update(i, a[i]); // i这个位置最大值是a[i],这里不是add,而是update
        }

        int x, y;
        while (m--) {
            scanf("%s %d %d", op, &x, &y);
            if (op[0] == 'U') { // 更新操作，要求把id为x的学生的成绩更改为y
                a[x] = y;       // ①将原数组修改
                update(x, y);   // ②将映射的树状数组修改,使得统计信息也相应修改完成
            } else
                printf("%d\n", query(x, y)); // 询问id从x到y(包括x,y)的学生当中，最大值是多少
        }
    }
    return 0;
}