python/TangDou/AcWing/NumTriangle/1015.md

AcWing 1015. 摘花生

一、题目描述　

Hello Kitty想摘点花生送给她喜欢的米老鼠

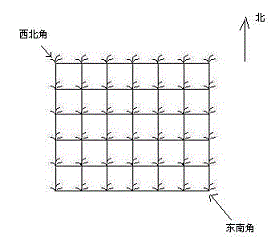
她来到一片有网格状道路的矩形花生地(如下图)，从 西北角 进去，东南角 出来

地里每个道路的交叉点上都有种着一株花生苗，上面有若干颗花生，经过一株花生苗就能摘走该它上面所有的花生

Hello Kitty只能 向东 或 向南 走，不能 向西 或 向北 走

问Hello Kitty最多能够摘到多少颗花生

输入格式 第一行是一个整数T，代表一共有多少组数据。

接下来是T组数据。

每组数据的第一行是两个整数，分别代表花生苗的行数R和列数 C。

每组数据的接下来R行数据，从北向南依次描述每行花生苗的情况。每行数据有C个整数，按从西向东的顺序描述了该行每株花生苗上的花生数目M。

输出格式 对每组输入数据，输出一行，内容为Hello Kitty能摘到得最多的花生颗数。

数据范围 1≤T≤100,1≤R,C≤100,0≤M≤1000

输入样例：

2
2 2
1 1
3 4
2 3
2 3 4
1 6 5

输出样例：

8
16

二、DP分析

状态表示 f[i][j]: 小猫可在出现的每个位置(x,y), 策略：面向答案编程， 从(1,1)走到(x,y)有多条路线，我们设f(x,y)为所有路线中 花生数量之和 最大值

状态转移

\large f[i][j]=max(f[i-1][j],f[i][j-1])+w[i][j]

填充顺序 观察状态转移方程，发现： ① 由于是一个二维状态表示，所以可以理解为是一个二维表，需要对二维表进行数据填充。 ② 第i行依赖第i-1行，第j列，依赖j-1列，所以，考虑从上到下，从左到右，就是先处理i,j中小的，再处理大的，可以形成递推依赖。

初始值 观察状态转移方程，知道f[1][1]=w[1][1]

答案 最终我们要计算的是在东南角时可以获取到的最多花生数，即f[n][m]。

三、二维DP写法

#include <bits/stdc++.h>

using namespace std;
const int N = 110;
int w[N][N];
int f[N][N];
int n, m;
int main() {
    int T;
    cin >> T;
    while (T--) {
        memset(f, 0, sizeof f);
        cin >> n >> m;

        for (int i = 1; i <= n; i++)
            for (int j = 1; j <= m; j++)
                cin >> w[i][j];

        for (int i = 1; i <= n; i++)
            for (int j = 1; j <= m; j++)
                // 递推的出发点，采用特判的办法手动维护，其它的靠关系式递推完成
                // 之所以这样对起点进行初始化，是因为只有这样才能保障逻辑自洽
                if (i == 1 && j == 1)
                    f[i][j] = w[i][j];
                else
                    f[i][j] = max(f[i - 1][j], f[i][j - 1]) + w[i][j];

        printf("%d\n", f[n][m]);
    }
    return 0;
}

四、一维DP写法

从二维降一维时，发现每个数据，只依赖于它上一行的同列数据，和同一行的左侧数据，也就是可以概括为依赖于 左+上。而采用一维进行记录状态时，f[i-1]表示的是f[i]的左侧供给数据，f[i]描述的是上一行的同列供给数据，两者PK就可以覆盖掉当前值。

#include <bits/stdc++.h>

using namespace std;
const int N = 110;
int w[N][N];
int f[N];
int n, m;
int main() {
    int T;
    scanf("%d", &T);
    while (T--) {
        memset(f, 0, sizeof f);
        scanf("%d %d", &n, &m);
        for (int i = 1; i <= n; i++)
            for (int j = 1; j <= m; j++)
                scanf("%d", &w[i][j]);

        for (int i = 1; i <= n; i++)
            for (int j = 1; j <= m; j++)
                if (i == 1 && j == 1) // 递推的出发点，采用特判的办法手动维护，其它的靠关系式递推完成
                    f[j] = w[i][j];
                else
                    f[j] = max(f[j], f[j - 1]) + w[i][j];

        printf("%d\n", f[m]);
    }
    return 0;
}

五、深搜写法

#include <bits/stdc++.h>

using namespace std;
//通过了 2/10个数据
const int N = 110;
int w[N][N];
int n, m;
int dfs(int x, int y) {
    if (x == n && y == m) return w[n][m];
    if (x > n || y > m) return 0;
    return max(dfs(x + 1, y), dfs(x, y + 1)) + w[x][y];
}
int main() {
    int T;
    cin >> T;
    while (T--) {
        cin >> n >> m;
        for (int i = 1; i <= n; i++)
            for (int j = 1; j <= m; j++)
                cin >> w[i][j];
        printf("%d \n", dfs(1, 1));
    }
    return 0;
}

不使用记忆化的深搜是不可以原谅的，速度太慢！究其原因应该是存在大量重复计算，比如dfs(3,5)，每次都计算一遍，性能要是好了就怪了，也就是说，我们如果想要使用dfs,就一定要思考使用数组完成记忆化，否则就别用。

六、深搜+记忆化

#include <bits/stdc++.h>

using namespace std;
const int N = 110;
int w[N][N];
int n, m;
int f[N][N];
int dfs(int x, int y) {
    if (f[x][y]) return f[x][y];
    if (x == n && y == m) return w[n][m];
    if (x > n || y > m) return 0;
    f[x + 1][y] = dfs(x + 1, y);
    f[x][y + 1] = dfs(x, y + 1);

    return f[x][y] = max(f[x + 1][y], f[x][y + 1]) + w[x][y];
}
int main() {
    int T;
    cin >> T;
    while (T--) {
        memset(f, 0, sizeof f);
        cin >> n >> m;
        for (int i = 1; i <= n; i++)
            for (int j = 1; j <= m; j++)
                cin >> w[i][j];
        printf("%d \n", dfs(1, 1));
    }
    return 0;
}

七、理解与感悟

1、递推关系式(状态转移方程)

在一般的局面下 ，比如现在处在(i,j)这个位置上时，思考如何给这个位置确定最佳的花生数量,显然是从左侧花生数量和上侧花生数量取一个max，再加上当前位置的花生数量即可完成填充：

\large f[i][j] = max(f[i - 1][j], f[i][j - 1]) + w[i][j]

2、递推起点和终点

有了递推式，才会思考哪里是递推起点和终点。西北角进入矩阵，东南角出去，很明显本题的起点是(1,1)，终点是(n,m)

• 起点f[1][1]：此处是入口，无法从其它位置转移而来，本身花生数就是最大数量，即f[1][1]=w[1][1]

• 终点f[n][m]：此处是出口，是答案，是结果，它的值需要走状态转移方程来确定

3、递推顺序

有了递推关系式和起点的基础，我们的目标就是通过递推计算，获取到f[n][m]的值，使用 瞪眼大法 (观察法),我们知道当前状态计算需要 上一行的同列数据 与 同行的前列数据，也就是在计算当前状态之前，务必保证它的上一行同列数据和同行前列数据完成填充工作，而双重循环，从上到下，从左到右 的枚举顺序，恰好可以满足这个要求！理解这一点非常重要，后面我们继续学习的动态规划问题，大家将会看到多维状态下，多层循环的枚举次序，其实 本质上都是为了填表。

4、与搜索的区别

• 动态规划f[i,j]含义：从起点走到(i,j)，可以取得的最大价值,随地随地都知道当前的值。

• 搜索dfs(i,j)含义：从(i,j)出发，到终点时可以获得的最大价值,现在的值需要以后的值确定才能知道。