python/TangDou/AcWing/BeiBao/9.md

##AcWing 9. 分组背包问题

一、题目描述

有 N 组物品和一个容量是 V 的背包。

每组物品有若干个，同一组内的物品最多只能选一个。 每件物品的体积是 v_{ij}，价值是 w_{ij}，其中 i 是组号，j 是组内编号。

求解将哪些物品装入背包，可使物品总体积不超过背包容量，且总价值最大。

输出最大价值。

输入格式 第一行有两个整数 N，V，用空格隔开，分别表示物品组数和背包容量。

接下来有 N 组数据：

每组数据第一行有一个整数 S_i，表示第 i 个物品组的物品数量； 每组数据接下来有 S_i 行，每行有两个整数 v_{ij},w_{ij}，用空格隔开，分别表示第 i 个物品组的第 j 个物品的体积和价值；

输出格式 输出一个整数，表示最大价值。

数据范围 0<N,V≤100

0<S_i≤100

0<v_{ij},w_{ij}≤100

输入样例

3 5
2
1 2
2 4
1
3 4
1
4 5

输出样例：

8

二、解题思路

直接上 分组背包 的 闫氏DP分析法

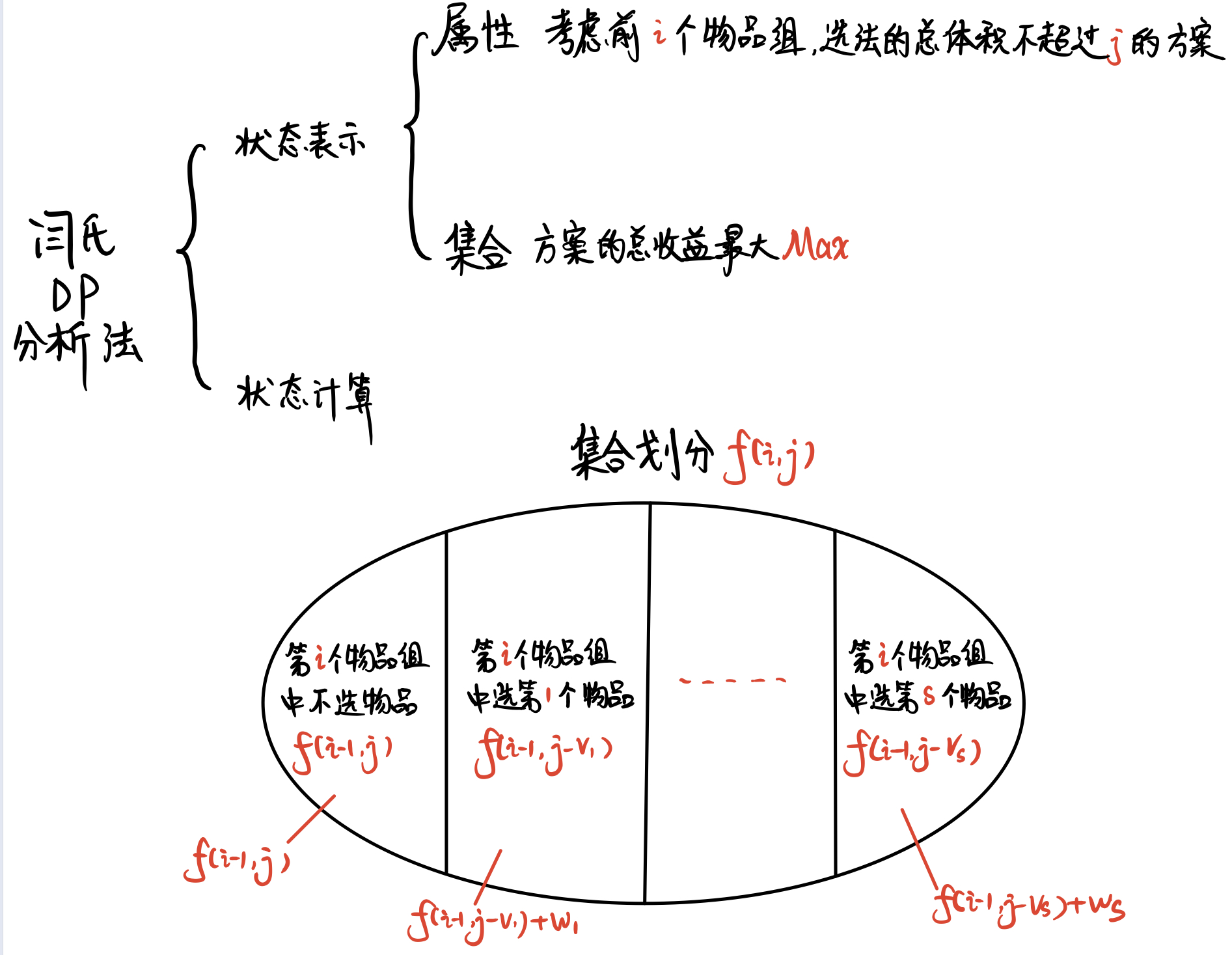
初始状态 ：f[0][0]

目标状态 ：f[N][M]

状态表示

f[i][j] 从前 i 组物品中选择且总体积不大于 j 的最大价值

状态计算

针对第 i 组物品，将整个状态划分成 s[i]+1 类：

• 第i组物品一个都不要：f[i][j] = f[i-1][j]
• 选第 i 组物品的第一个物品：f[i][j] = f[i-1][j-v[1]]+w[1]
• 选第 i 组物品的第二个物品：f[i][j] = f[i-1][j-v[2]]+w[2]
• 选第 i 组物品的第 k 个物品：f[i][j] = f[i-1][j-v[k]]+w[k]

状态转移

$$\large f[i][j]=max(f[i][j], f[i-1][j-v[k]]+w[k])), k=0, 1, 2,...,s[

状态初始化

f[0][0\sim m] = 0 表示在选择 0 件物品时对于任何体积来讲，其最大价值均为 0

同理，分组背包问题也是可以从二维优化到一维的。其实只需要谨记两点：

• 当前状态需要用上层状态转移时，从大到小枚举体积
• 当前状态需要用本层状态转移时，从小到大枚举体积

总结： 每个组中可以一个也不选，选也只能选择1个

三、二维数组版本

#include <bits/stdc++.h>

using namespace std;

const int N = 110;
int n, m;
int f[N][N], v[N][N], w[N][N], s[N];

int main() {
    cin >> n >> m;
    for (int i = 1; i <= n; i++) {
        cin >> s[i]; // 第i个分组中物品个数
        for (int j = 1; j <= s[i]; j++)
            cin >> v[i][j] >> w[i][j]; // 第i个分组中物品的体积和价值
    }

    for (int i = 1; i <= n; i++)
        for (int j = 0; j <= m; j++) {
            for (int k = 0; k <= s[i]; k++)
                if (j >= v[i][k])
                    f[i][j] = max(f[i][j], f[i - 1][j - v[i][k]] + w[i][k]); // 枚举每一个PK一下大小
        }
    // 输出打表结果
    printf("%d", f[n][m]);
    return 0;
}

四、一维数组版本

#include <bits/stdc++.h>

using namespace std;
const int N = 110;

int n, m;
int v[N][N], w[N][N], s[N];
int f[N];

int main() {
    cin >> n >> m;

    for (int i = 1; i <= n; i++) {
        cin >> s[i];
        for (int j = 1; j <= s[i]; j++)
            cin >> v[i][j] >> w[i][j];
    }

    for (int i = 1; i <= n; i++)
        for (int j = m; j >= 0; j--)
            for (int k = 1; k <= s[i]; k++)
                if (j >= v[i][k])
                    f[j] = max(f[j], f[j - v[i][k]] + w[i][k]);

    printf("%d\n", f[m]);
    return 0;
}