python/TangDou/AcWing/BeiBao/278.md

##AcWing 278. 数字组合

【总结】背包问题的至多/恰好/至少

一、题目描述

给定 N 个正整数 A_1,A_2,…,A_N，从中选出若干个数，使它们的和为 M，求有多少种选择方案。

输入格式

第一行包含两个整数 N和 M。

第二行包含 N个整数，表示 A_1,A_2,…,A_N。

输出格式

包含一个整数，表示可选方案数。

数据范围 1≤N≤100,1≤M≤10000,1≤A_i≤1000,答案保证在 int 范围内。

输入样例：

4 4
1 1 2 2

输出样例：

3

二、01背包求解恰好装满方案数

分析

对于本题我们可以把每个 正整数 看作是一个 物品

正整数 的值就是 物品 的 体积

我们方案选择的 目标 是最终 体积 恰好为 m 时的 方案数

于是本题就变成了 01背包求解方案数 的问题了

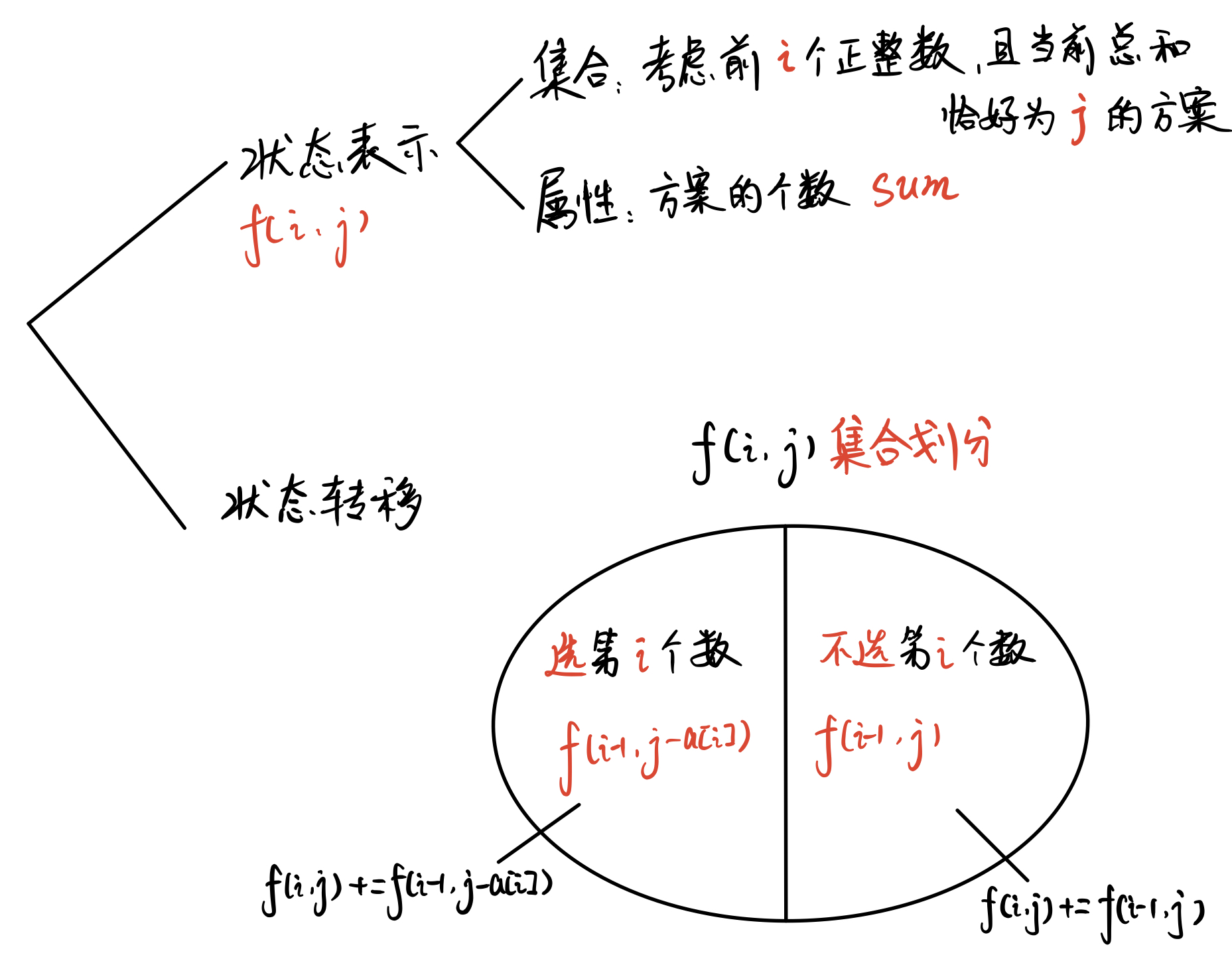
状态表示

f[i][j]:考虑前i个数，当前总和 恰好 为j时，方案数量是多少。

状态转移

• 不选i：\large f[i][j] += f[i-1][j]
• 选 i： \large f[i][j] += f[i-1][j-v[i]]

初始状态：

f[i][0]=1

解释：不管你让我从多少个物品中选择，只要是背包容量是0,那么方案就只有1种，就是，啥都不要。

目标状态

f[n][m]

时间复杂度

O(n×m)

三、二维代码

#include <bits/stdc++.h>

using namespace std;
const int N = 110;
const int M = 10010;
int n, m;
int v;
int f[N][M];

int main() {
    cin >> n >> m;

    for (int i = 0; i <= n; i++) f[i][0] = 1; // base case

    for (int i = 1; i <= n; i++) {
        cin >> v;
        for (int j = 1; j <= m; j++) {
            // 从前i-1个物品中选择，装满j这么大的空间，假设方案数是5个
            // 那么，在前i个物品中选择，装满j这么大的空间，方案数最少也是5个
            // 如果第i个物品，可以选择，那么可能使得最终的选择方案数增加
            f[i][j] = f[i - 1][j];
            // 增加多少呢？前序依赖是：f[i - 1][j - v]
            if (j >= v) f[i][j] += f[i - 1][j - v];
        }
    }
    // 输出结果
    printf("%d\n", f[n][m]);
    return 0;
}

四、一维代码

#include <bits/stdc++.h>

using namespace std;
const int N = 10010;

int n, m;
int v;
int f[N]; // 在前i个物品，体积是j的情况下，恰好装满的方案数

int main() {
    cin >> n >> m;

    // 体积恰好j, f[0]=1, 其余是0
    f[0] = 1;
    for (int i = 1; i <= n; i++) {
        cin >> v;
        for (int j = m; j >= v; j--)
            f[j] += f[j - v];
    }
    printf("%d\n", f[m]);
    return 0;
}

###　五、常见问题

Q:如果讨论的不是数量，而是最大价值，有什么区别呢？

A:我们可以将结论推广到不同属性的情况下，本题的属性是数量，但如果是最大价值呢？ 我们不难得到需要将f[0]初始化为0，f[1\sim n]初始化为负无穷

为什么要这样设置呢？因为每一个新状态，都需要知道它可以从哪些旧状态转移而来，如果上一个状态是合法的，那么有可能从上一个状态转移而来，但如何标识上一个状态是不是合法呢？比如如果初始化状态值是0，并且上一个状态是0,表示的是目前的最大值，那要是不合法呢？不好说啊，为什么呢？

• 上一个状态不合法，没有状态转移过来
• 上一个状态合法，因为有负数等原因，造成最大值确实为0

这就很难办的，是吧。搞不清楚上一个状态是不是合法，我就没法决策是不是可以从它转移过来，我必须想办法对合法与不合法状态进行区分，是吧？

办法就是初始化为-INF,再转移啥负值，也不可能小于-INF,所以，很容易就区分开了是不是正常合法状态，还是从来就没有到达过的不合法状态。