python/TangDou/AcWing/BeiBao/1023.md

##AcWing 1023. 买书

【总结】背包问题的至多/恰好/至少

一、题目描述

小明有 m 块钱，现有 10 元， 20 元， 50 元， 100 元 的书

每本书可以 购买多次，求小明有 多少种 买书 方案

注：钱需要花完

输入格式

一个整数 n，代表总共钱数。

输出格式

一个整数，代表选择方案种数。

数据范围

0≤n≤1000

输入样例1：

20

输出样例1：

2

输入样例2：

15

输出样例2：

0

输入样例3：

0

输出样例3：

1

二、分析

一共有 n 个物品，每个物品有体积 v_i，价值 w_i，每个物品能够选多次

求总体积恰好是m的方案数

这是一道 裸的完全背包问题求解方案数

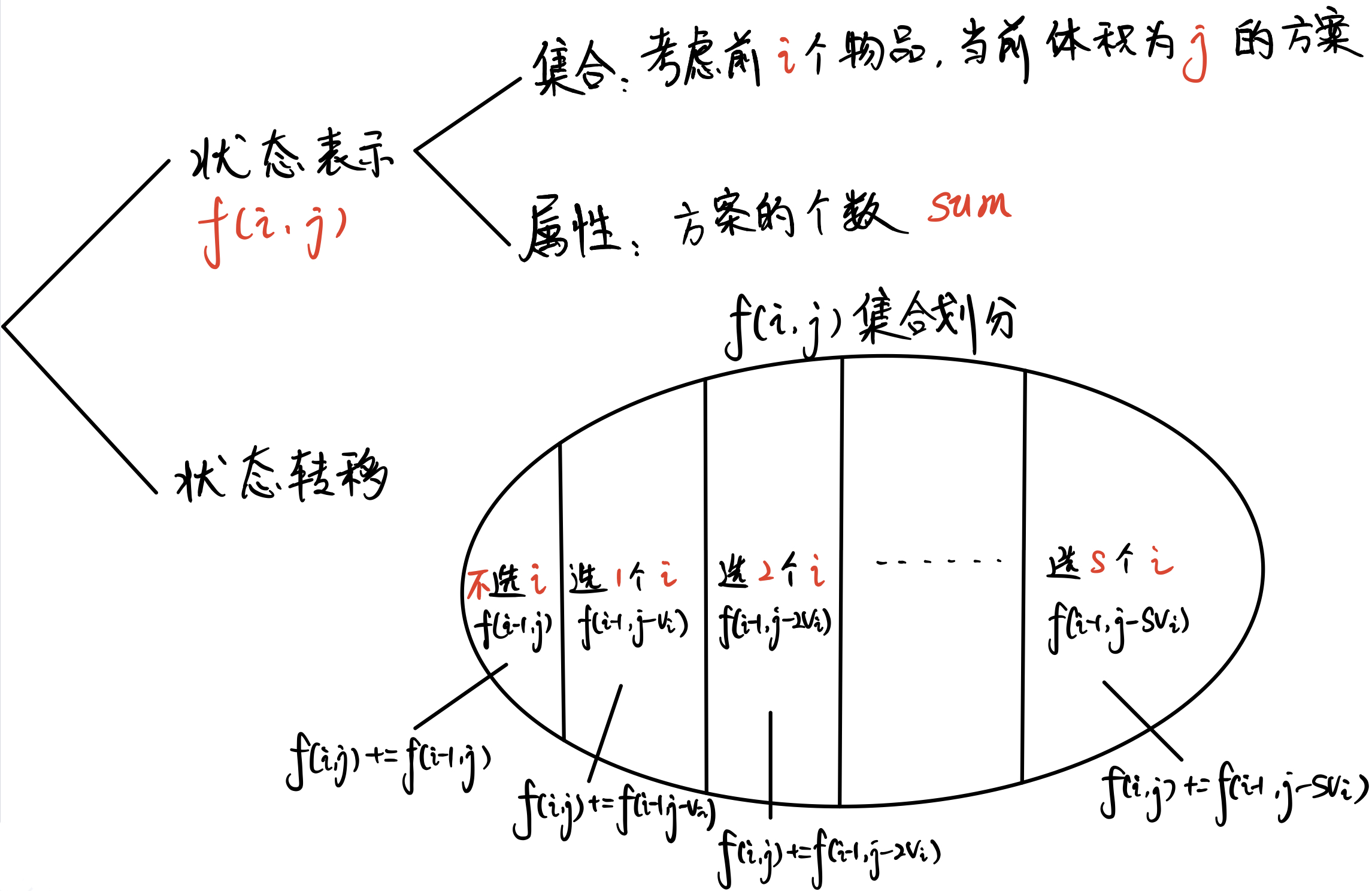
闫氏DP分析法

状态表示——集合：f[i][j] 表示考虑前i个数字，且总数字和 恰好 j的集合下能获得的方案数。

状态表示——属性：因为是求方案数，故为 count。

状态计算——集合划分：考虑第 i 个数选不选。

• 不选或选不了（剩余数量不够 j<a[i]）：f[i−1][j]。
• 选：f[i][j−a[i]]。

初始状态：f[0][0]

目标状态：f[n][m]

二、朴素版本

时间复杂度：O(n^2 \times m)

#include <bits/stdc++.h>

using namespace std;

const int N = 5;
const int M = 1010;

int v[N] = {0, 10, 20, 50, 100}; // 每种货币，下标从1开始
int n, m;                        // 货币种类，钱数
int f[N][M];                     // 前i种物品，体积恰好是j的情况下的最大值

// 完全背包
int main() {
    n = 4;
    cin >> m;
    // 前0种物品，体积是0的情况下只有一种方案
    // 一般询问方案数的问题f[0]都会设置为1
    //  Q:那20元钱呢？不买；买两本10块的；每一本20的。三种呀
    //  A:题目说的全部，钱要花完
    f[0][0] = 1;
    for (int i = 1; i <= n; i++)                // 每个物品
        for (int j = 0; j <= m; j++)            // 每个体积
            for (int k = 0; v[i] * k <= j; k++) // 个数
                f[i][j] += f[i - 1][j - v[i] * k];
    printf("%d\n", f[n][m]);
    return 0;
}

三、完全背包—经典优化

使用瞪眼大法，观察 f(i,j) 的 状态转移方程 进行变形 尝试找出f(i,j)与它的前序f(i,j-v_i)之间的关联关系，看看能不能实现f(i,j-v_i)->f(i,j)的迁移：

\large f(i,j)=f(i-1,j)+f(i-1,j-v_i)+...+f(i-1,j-s\cdot v_i)①

\large f(i,j-v_i)=　　　f(i-1,j-v_i)+...+f(i-1,j-s\cdot v_i)②

注：把体积j-v_i代入①式,就可以得到 ②式

Q:①和②中的s是一个值吗，为什么？ 答：是一个值的。原因可以从事情本质出发，思考一下s\cdot v_i的含义是什么:就是在j这么大的空间限制下，最多可以装多少个i物品，当然是同一个个数值s了。

由上述两个等式可以获得如下递推式：

\LARGE f(i,j)=f(i−1,j)+f(i,j−v_i)

把这个等式作为 状态转移方程 ，就可以把时间复杂度优化到 O(n \times m) 同时，观察到该 转移方程 对于第 i 阶段的状态，只会使用第 i-1 层和第 i 层的状态

因此我们也可以采用 01背包 的 空间优化方案

时间复杂度：O(n×m) 空间复杂度：O(m)

二维优化版本

#include <bits/stdc++.h>

using namespace std;
const int N = 1010;
int v[5] = {0, 10, 20, 50, 100};
int f[5][N];

int main() {
    int m;
    cin >> m;
    // 前0种物品，体积是0的情况下只有一种方案
    f[0][0] = 1;
    for (int i = 1; i <= 4; i++)
        for (int j = 0; j <= m; j++) {
            f[i][j] = f[i - 1][j];
            if (v[i] <= j) f[i][j] += f[i][j - v[i]];
        }
    printf("%d\n", f[4][m]);
    return 0;
}

一维优化解法

#include <bits/stdc++.h>

using namespace std;
const int N = 1010;
int v[5] = {0, 10, 20, 50, 100};
int f[N];

// 体积限制是恰好是，因此需要初始化f[0][0]为合法解1，其他位置为非法解0。
int main() {
    int m;
    cin >> m;
    // 前0种物品，体积是0的情况下只有一种方案
    f[0] = 1;
    for (int i = 1; i <= 4; i++)
        for (int j = v[i]; j <= m; j++)
            f[j] += f[j - v[i]];
    // 输出
    printf("%d\n", f[m]);
    return 0;
}