|
|
##[$AcWing$ $1021$. 货币系统 ](https://www.acwing.com/problem/content/1023/)
|
|
|
|
|
|
**[【总结】背包问题的至多/恰好/至少](https://www.cnblogs.com/littlehb/p/15847138.html)**
|
|
|
|
|
|
### 一、题目描述
|
|
|
给你一个$n$种面值的货币系统,求组成面值为$m$的货币有多少种方案。
|
|
|
|
|
|
**输入格式**
|
|
|
第一行,包含两个整数$n$和$m$。
|
|
|
|
|
|
接下来$n$行,每行包含一个整数,表示一种货币的面值。
|
|
|
|
|
|
**输出格式**
|
|
|
共一行,包含一个整数,表示方案数。
|
|
|
|
|
|
**数据范围**
|
|
|
$n≤15,m≤3000$
|
|
|
|
|
|
**输入样例**:
|
|
|
```cpp {.line-numbers}
|
|
|
3 10
|
|
|
1
|
|
|
2
|
|
|
5
|
|
|
```
|
|
|
|
|
|
**输出样例**:
|
|
|
```cpp {.line-numbers}
|
|
|
10
|
|
|
```
|
|
|
|
|
|
### 二、题目解析
|
|
|
本题与上一题买书问题基本一模一样,只是方案数可能很大,需要用`long long`来存储。
|
|
|
|
|
|
**状态表示**
|
|
|
$f[i][j]$: 用前$i$种面值的货币组成面值 **恰好** 为$j$的方案数
|
|
|
|
|
|
**状态转移方程**
|
|
|
$$\large f[i][j] = f[i-1][j] + f[i][j-v]$$
|
|
|
边界状态为$f[i][0] = 1$
|
|
|
|
|
|
|
|
|
### 三、实现代码
|
|
|
```cpp {.line-numbers}
|
|
|
#include <bits/stdc++.h>
|
|
|
|
|
|
using namespace std;
|
|
|
typedef long long LL;
|
|
|
|
|
|
const int N = 20;
|
|
|
const int M = 3010;
|
|
|
int n, m;
|
|
|
LL v[N];
|
|
|
LL f[M];
|
|
|
|
|
|
int main() {
|
|
|
cin >> n >> m;
|
|
|
f[0] = 1;
|
|
|
for (int i = 1; i <= n; i++) {
|
|
|
cin >> v[i];
|
|
|
for (int j = v[i]; j <= m; j++)
|
|
|
f[j] += f[j - v[i]];
|
|
|
}
|
|
|
printf("%lld\n", f[m]);
|
|
|
return 0;
|
|
|
}
|
|
|
```
|
|
|
|
|
|
### 四、 重复组合公式
|
|
|
|
|
|
**计算公式**
|
|
|
从$n$个不同的元素每次取出$r$个元素的 **允许重复** 组合总数为:
|
|
|
$$\large F(n,r)=C_{n+r-1}^r$$
|
|
|
|
|
|
**证明**
|
|
|
- **插板法原理**
|
|
|
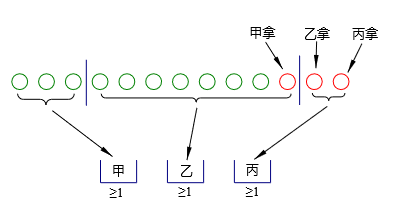
考虑这样一个问题:把$10$个苹果分给$3$人,每人至少分$1$个,有多少种分法?
|
|
|
|
|
|
|
|
|
我们这样考虑:把$10$个苹果分给$3$人,我们就要在$9$个空格里面插入$2$块板,就会分为$3$部分,且每部分都至少$1$个,故有$C_9^{2}$种。如图的插板方式,就是甲分$3$个,乙分$5$个,丙分$2$个。
|
|
|
|
|
|
- **变式$1$**
|
|
|
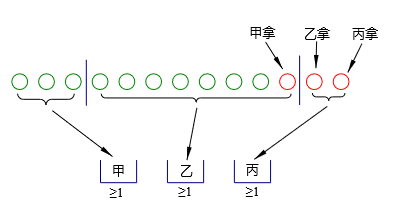
将上述问题略加变化:把$10$个苹果分给$3$人,每人可以不分,有多少种分法?
|
|
|
|
|
|
这时我们要向第一种情况转化,可以假设甲、乙、丙三人本来都有苹果,他们都拿一个苹果出来,一起分,这样他们每人就至少要一个苹果了。
|
|
|
|
|
|
|
|
|
|
|
|
我们就要在$9+3=12$个空格里面插入$2$块板,就会分为$3$部分,且每部分都至少$1$个,故有$C_{12}^2$种。如图的插板方式,就是甲分$3-1=2$个,乙分$8-1=7$个,丙分$2-1=1$个。
|
|
|
|
|
|
- **变式$2$**
|
|
|
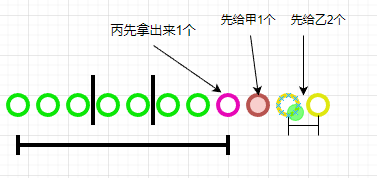
继续深入讨论:把$10$个苹果分给$3$人,甲至少要$2$个,乙至少要$3$个,丙可以不要,有多少种分法?
|
|
|
|
|
|
我们还要向第一种情况转化,可以假设先给甲$1$个、给乙$2$个、而丙自己先拿出来$1$个,这样他们分余下的苹果时,**每人至少要一个苹果就可以了**。
|
|
|
|
|
|
|
|
|
我们就要在$9-3+1=7$个空格里面插入$2$块板,就会分为$3$部分,且每部分都至少$1$个,故有$C_7^2$种。如图的插板方式,就是甲分$3+1=4$个,乙分$2+2=4$个,丙分$3-1=2$个。
|
|
|
> **[高中数学题练习链接](https://mp.weixin.qq.com/s?__biz=MzU5OTQ2NzIzNw==&mid=2247498459&idx=1&sn=7309883315d9139a0e70a73e041b2183&chksm=feb6cf51c9c146475e12aab57f88c13f4c33fe214ca1d05a7aaff4f9df4fb257c4ba795f9a94&scene=27)**
|
|
|
|
|
|
回到本题,理解为 **变式$2$**, 每个盒子里可以没有被选择的数字,也就是$0$个,为了适应 **隔板法**,通过构造的办法,我们认为每个盒子先拿出来一个,这样,最起码它最后能有$1$个,也就是$n+r$个小球,此时,可以放隔板的位置就是$n+r-1$个,需要选择的位置数是$r$:
|
|
|
$$\large F(n,r)=C_{n+r-1}^r$$
|
|
|
|
|
|
证毕
|
|
|
|
|
|
**利用公式估算数据范围**
|
|
|
$$\LARGE C_{3000+15-1}^{3000}=C_{3014}^{14}=\frac{3014!}{14!\times 3000!}=\frac{3001\times ... \times 3014}{14!}$$
|
|
|
|
|
|
|
|
|
**最坏的情况**
|
|
|
上面我们的思考和假设,都是 **一样的小球**,也就是对应着所以货币的面额都是$1$,要求组合成价值$3000$的货币,每种货币无个数限制。
|
|
|
|
|
|
由于题目中说了,每种货币的价值并不相同,也就是上面论述的每个盒子里面不能随意放入最多$r$个小球,受每个盒子上限不同的限制。根据公式求出的数值,肯定是大于真实的数值。
|
|
|
|
|
|
按公式计算出的数值,要大于`int`的范围,如果此题数据为最坏情况,那么`long long`也会爆掉。
|
|
|
|