python/TangDou/CSP-J/J2_2020/3.md

[CSP-J2020] 表达式

[CSP-J2020]表达式-洛谷

思路：后缀表达式 用 栈 模拟运算

不做任何处理，暴力可以得30分

一、题目解析

先看样例：x_1\ x_2 \ \& \ x_3 \ | 这是一个后缀表达式形式，

可以用测试用例给同学们讲解一下测试用例，包括第一次计算和修改某个值后的计算。

一、暴力建树求值

#include <bits/stdc++.h>

using namespace std;
const int N = 1000010, M = N << 1;
#define ls e[h[u]]
#define rs e[ne[h[u]]]

int n;          // n个变量
int a[N];       // 每个变量对应的数值
char c[N];      // 操作符
stack<int> stk; // 模拟栈

// 链式前向星
int e[M], h[N], idx, w[M], ne[M];
void add(int a, int b, int c = 0) {
    e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx++;
}

// 表示式求值
int dfs(int u) {
    if (u <= n) return a[u]; // 如果是叶子，是变量，是数值，返回真实值
    if (c[u] == '!')
        a[u] = !dfs(ls); //! 只有一个儿子，所以e[h[u]]就是儿子的节点号,对儿子返回的值取反就是当前节点的返回值,同时实现了记忆化
    else {
        //&和|有两个儿子，分别是e[h[u]]和e[ne[h[u]]]
        if (c[u] == '&')
            a[u] = dfs(ls) & dfs(rs); // 计算
        else
            a[u] = dfs(ls) | dfs(rs); // 计算
    }
    return a[u]; // 返回
}

// https://www.luogu.com.cn/problem/P7073
// 20个测试点，可以过掉6个
int main() {
#ifndef ONLINE_JUDGE
    freopen("P7073.in", "r", stdin);
    // freopen(".out", "w", stdout);
#endif

    memset(h, -1, sizeof h); // 初始化链式前向星

    string s;
    getline(cin, s);
    cin >> n;
    for (int i = 1; i <= n; i++) cin >> a[i]; // x1,x2,x3的真实值

    // 数字占了前n个节点,比如x1占用了1号节点，x2占用了2号节点
    // n+1开始留给操作符
    int idx = n;

    for (int i = 0; i < s.size(); i++) {
        if (s[i] == ' ') continue; // 放过空格
        if (s[i] == 'x') {         // 发现是变量标识
            int k = 0;
            i++;
            while (i < s.size() && isdigit(s[i])) k = k * 10 + s[i++] - '0'; // 取得是 x?,比如?=124
            stk.push(k);                                                     // x124存到图中，节点号就是124
        } else if (s[i] == '!') {
            c[++idx] = s[i];     // 记录操作符数组,n+1是第一个操作符对应的树中节点号
            add(idx, stk.top()); // 操作符向数字连一条边
            stk.pop();
            stk.push(idx);   // 将操作符也要入栈
        } else {             // 如果是 & 或 |
            c[++idx] = s[i]; // 记录idx号节点是 & 或 | 或 !
            int a = stk.top();
            stk.pop();
            int b = stk.top();
            stk.pop();
            add(idx, a), add(idx, b); // 1托2建边
            stk.push(idx);            // 将操作符也要入栈
        }
    }

    // 最后一个入栈的是根,根是一个操作符，叶子都是变量，是数值
    int root = stk.top();

    int q;
    cin >> q;
    while (q--) {
        int x;
        cin >> x;
        // 取反
        a[x] = !a[x];
        // 输出
        cout << dfs(root) << endl;
        // 回溯
        a[x] = !a[x];
    }
    return 0;
}

二、优化

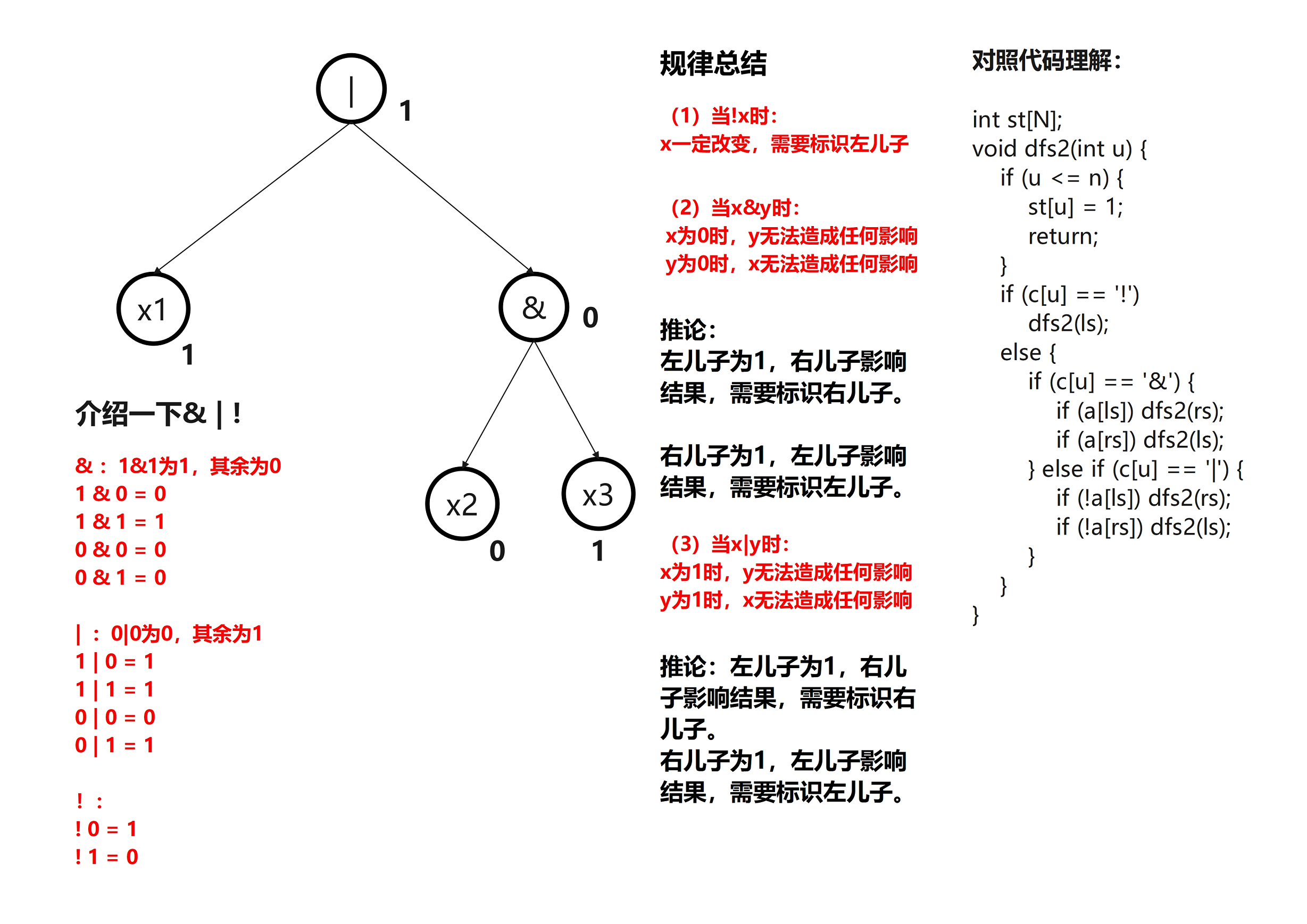
介绍一下\& | !

\& ：1\&1为1，其余为0 1 \& 0 = 0 1 \& 1 = 1 0 \& 0 = 0 0 \& 1 = 0

| : 0|0为0，其余为1 1 | 0 = 1 1 | 1 = 1 0 | 0 = 0 0 | 1 = 1

！： ! 0 = 1 ! 1 = 0

发现了吗？对于\&和|都有一些运算数 无论怎样改变，只要 另一个运算数不变，它们 运算的值也不变。

有以下结论：

当x\&y时： x为0时，y无法造成任何影响 y为0时，x无法造成任何影响

当x|y时： x为1时，y无法造成任何影响 y为1时，x无法造成任何影响

当!x时： x一定改变

那么我们可以把 可以造成影响的数 打上一个 st标记

#include <bits/stdc++.h>

using namespace std;
// 重定义左右儿子
#define ls e[h[u]]
#define rs e[ne[h[u]]]
const int N = 1000010, M = N << 1;

int n;
int a[N];       // 每个变量的数值，0或1
char c[N];      // 记录 c[i]是哪种操作符，比如　& | !,如果是变量x1,x2,x3 ... 节点,则默认值是0
stack<int> stk; // 建立表示树用到的栈

// 邻接表
int e[M], h[N], idx, ne[M];
void add(int a, int b) {
    e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}

// 异或表示式树求值计算
int dfs1(int u) {
    if (u <= n) return a[u];
    if (c[u] == '!')
        a[u] = !dfs1(ls);
    else {
        if (c[u] == '&')
            a[u] = dfs1(ls) & dfs1(rs);
        else if (c[u] == '|')
            a[u] = dfs1(ls) | dfs1(rs);
    }
    return a[u];
}

// 标记以u为根的子树，每个数值结点（叶子结点）变更，是否对整体结果有影响,true:有影响，false:无影响
int st[N];
void dfs2(int u) {
    if (u <= n) {  // 叶子节点
        st[u] = 1; // 这个叶子节点的修改，对整体结果有影响。如果无法到达这个位置，就表示无影响
        return;
    }
    if (c[u] == '!') // 非运算符,左儿子的变化会影响结果
        dfs2(ls);
    else {
        if (c[u] == '&') {
            // ① 如果左儿子是1，右儿子会影响结果
            // ② 如果右儿子是1，左儿子会影响结果
            if (a[ls]) dfs2(rs);
            if (a[rs]) dfs2(ls);
        } else if (c[u] == '|') {
            // ③ 如果左儿子是0，右儿子会影响结果
            // ④ 如果右儿子是0，左儿子会影响结果
            if (!a[ls]) dfs2(rs);
            if (!a[rs]) dfs2(ls);
        }
    }
}

int main() {
    string s;
    getline(cin, s);

    cin >> n;
    for (int i = 1; i <= n; i++) cin >> a[i];

    // 初始化
    memset(h, -1, sizeof h);

    // 放过前n个，从n+1开始
    int idx = n;

    for (int i = 0; i < s.size(); i++) {
        if (s[i] == ' ') continue;
        if (s[i] == 'x') {
            int k = 0;
            i++;
            while (i < s.size() && isdigit(s[i])) k = k * 10 + s[i++] - '0';
            stk.push(k);
        } else if (s[i] == '!') {
            c[++idx] = s[i];
            add(idx, stk.top());
            stk.pop();
            stk.push(idx);
        } else {
            c[++idx] = s[i];
            int x = stk.top();
            stk.pop();
            int y = stk.top();
            stk.pop();
            add(idx, x), add(idx, y);
            stk.push(idx);
        }
    }

    int root = stk.top();

    // 计算初始值,因为后面的修改，可能不改变原始值，也可能改变原始值
    // 首先我们要计算出每个操作符所在位置的原始结果值
    int res = dfs1(root);

    // 标记每个数值结点（叶子结点）变更，是否对整体结果有影响,true:有影响，false:无影响
    dfs2(root);

    // 处理q次询问
    int q;
    cin >> q;
    // 询问时查表即可,整个程序的时间复杂度为O(q)
    while (q--) {
        int x;
        cin >> x;
        if (st[x]) // 如果x被打过标记，那么它的变化将会影响根节点的值，对根节点异或1即可
            printf("%d\n", res ^ 1);
        else // 不会影响根节点的值
            printf("%d\n", res);
    }
    return 0;
}