|
|
[题解链接](https://blog.csdn.net/WillHou/article/details/127698013)
|
|
|
|
|
|
### [$CSP-J$ $2022$] 乘方
|
|
|
[P8813 [CSP-J 2022] 乘方(民间数据)](https://www.luogu.com.cn/problem/P8813)
|
|
|
|
|
|
题目要去判断$a^b$ 是否超过 $10^9$ 再根据结果进行输出。
|
|
|
|
|
|
本题需要注意数据范围,$1≤a,b≤10^9$。如果算出结果再比较的话会超过数据范围,可以在累乘的过程中判断是否超过$10^9$即可。
|
|
|
|
|
|
由于$10^9 < 2^{30}$所以最多循环$30$次就行。
|
|
|
<font color='red' size=4><b>
|
|
|
需要特判下$a$等于$1$的情况,不然$b$很大时,循环次数会过多。</b></font>
|
|
|
|
|
|
```cpp {.line-numbers}
|
|
|
#include <bits/stdc++.h>
|
|
|
|
|
|
using namespace std;
|
|
|
typedef long long LL;
|
|
|
int main() {
|
|
|
LL a, b, res = 1;
|
|
|
cin >> a >> b;
|
|
|
//需要对a==1进行特判,否则肯定会TLE一个点
|
|
|
if (a == 1) {
|
|
|
printf("%d\n", 1);
|
|
|
exit(0);
|
|
|
}
|
|
|
for (LL i = 1; i <= b; i++) {
|
|
|
res *= a;
|
|
|
if (res > 1e9) {
|
|
|
printf("%d\n", -1);
|
|
|
exit(0);
|
|
|
}
|
|
|
}
|
|
|
printf("%lld\n", res);
|
|
|
return 0;
|
|
|
}
|
|
|
```
|
|
|
|
|
|
### [$CSP-J$ $2022$] 解密
|
|
|
[P8814 [CSP-J 2022] 解密(民间数据)](https://www.luogu.com.cn/problem/P8814)
|
|
|
|
|
|
本题要求在给定 $n,e,d$ 的情况下求 $p,q$的值
|
|
|
|
|
|
已知:
|
|
|
|
|
|
① $n=p×q$
|
|
|
② $e\times d=(p-1)(q-1)+1$
|
|
|
|
|
|
上过初一的同学们看到上面的信息就明白了,这是一个二元一次方程组,需要把方程整理一下:
|
|
|
|
|
|
|
|
|
|
|
|
展开式子 ②:$e\times d=p\times q-(p+q)+2=n-(p+q)+2$
|
|
|
|
|
|
可得:$p+q=n-e\times d +2$ ③
|
|
|
|
|
|
|
|
|
整理一下:
|
|
|
|
|
|
$$
|
|
|
\large \left\{\begin{array}{cc}
|
|
|
n=p×q & ④ \\
|
|
|
p+q=n-e\times d +2 = m & ⑤
|
|
|
\end{array}\right.
|
|
|
$$
|
|
|
|
|
|
$n$和$m$再输入后已知,那么本题就是求一元二次方程解。
|
|
|
|
|
|
根据式子④:$\large q=\frac{n}{p}$
|
|
|
|
|
|
带入式子⑤: $\large p+\frac{n}{p}=m$
|
|
|
|
|
|
两边相乘并调整下位置:$\large p^2-mp+n=0$
|
|
|
|
|
|
求解$p$的值即可。
|
|
|
|
|
|
根据一元二次方程求解公式:$$x=\frac{-b \pm \sqrt{b^2-4ac}}{2a}$$
|
|
|
|
|
|
此时 $a=1,b=-m,c=n$
|
|
|
|
|
|
|
|
|
#### 无解判断
|
|
|
* 若 $b^2-4ac<0$ 则无解
|
|
|
* 因$p$为正整数,所以如果 $b \pm \sqrt{b^2-4ac}$ 无法整除 $2a$ 也是无解
|
|
|
|
|
|
其它则代入公式进行计算即可。
|
|
|
|
|
|
```cpp {.line-numbers}
|
|
|
#include <bits/stdc++.h>
|
|
|
using namespace std;
|
|
|
typedef long long LL;
|
|
|
|
|
|
LL n, d, e;
|
|
|
// p^2 -(n-e*d+2)p+n = 0
|
|
|
bool check(LL num) { //判断num是否时完全平方数
|
|
|
LL t = LL(sqrt(num));
|
|
|
return t * t == num;
|
|
|
}
|
|
|
int main() {
|
|
|
//文件输入
|
|
|
freopen("decode.in", "r", stdin);
|
|
|
//文件输出
|
|
|
freopen("decode.out", "w", stdout);
|
|
|
int k;
|
|
|
cin >> k;
|
|
|
|
|
|
while (k--) {
|
|
|
cin >> n >> d >> e;
|
|
|
LL b = e * d - n - 2;
|
|
|
LL a = 1, c = n;
|
|
|
|
|
|
//一元二次方程无解的情况
|
|
|
if (b * b < 4 * a * c) {
|
|
|
puts("NO");
|
|
|
continue;
|
|
|
}
|
|
|
|
|
|
LL t = b * b - 4 * a * c; // t需要是一个完全平方数
|
|
|
bool flag = false;
|
|
|
if (check(t) && (LL(-b + sqrt(t)) % (2 * a) == 0)) {
|
|
|
LL p = (-b - sqrt(t)) / (2 * a); //两个解,一个是+,另一个就是-,小的在前就是-,大的在后就是+
|
|
|
//所以这里将符号变了一下
|
|
|
LL q = n / p;
|
|
|
if (p) { // p是正整数,0或负数需要否掉
|
|
|
flag = true;
|
|
|
printf("%lld %lld\n", p, q);
|
|
|
}
|
|
|
}
|
|
|
if (!flag) puts("NO");
|
|
|
}
|
|
|
return 0;
|
|
|
}
|
|
|
```
|
|
|
|
|
|
### [$CSP-J$ $2022$] 逻辑表达式
|
|
|
[P8815 [CSP-J 2022] 逻辑表达式(民间数据)](https://www.luogu.com.cn/problem/P8815)
|
|
|
|
|
|
本题与 $NOIP2013$普及组复赛第二题《表达式求值》是亲属关系,
|
|
|
|
|
|
#### 关键词
|
|
|
中缀表达式转后缀表达式,后缀表达式求值
|
|
|
|
|
|
#### 前置试题
|
|
|
[$AcWing$ $3302$ 表达式求值](https://www.acwing.com/problem/content/3305/)
|
|
|
|
|
|
[【$2013$ $NOIP$普及组】表达式求值](http://ybt.ssoier.cn:8088/problem_show.php?pid=1962)
|
|
|
|
|
|
#### 1、中缀表达式转后缀表达式(四则运算+以空格隔开)
|
|
|
```cpp {.line-numbers}
|
|
|
#include <bits/stdc++.h>
|
|
|
using namespace std;
|
|
|
|
|
|
//中缀表达式转后缀表达式
|
|
|
/*
|
|
|
测试用例1:
|
|
|
a+b*c+(d*e+f)*g
|
|
|
|
|
|
答案:
|
|
|
abc*+de*f+g*+
|
|
|
|
|
|
|
|
|
测试用例2:
|
|
|
(6+3*(7-4))-8/2
|
|
|
|
|
|
答案:
|
|
|
6 3 7 4 - * + 8 2 / -
|
|
|
|
|
|
测试用例3:
|
|
|
(24*(9+6/38-5)+4)
|
|
|
答案:
|
|
|
24 9 6 38 / + 5 - * 4 +
|
|
|
*/
|
|
|
|
|
|
// 也可以写成下面的形式:(因为在unordered_map中,查找不到的字符,会返回默认值0,所以(=0这句加与不加是一样的 )
|
|
|
// unordered_map<char, int> h{{'+', 1}, {'-', 1}, {'*', 2}, {'/', 2}, {'(', 0}};
|
|
|
unordered_map<char, int> h{{'+', 1}, {'-', 1}, {'*', 2}, {'/', 2}};
|
|
|
string s; //输入的中缀表达式 s:source
|
|
|
string t; //后缀的结果表达式 t:target
|
|
|
stack<char> stk; //使用到的操作符+数字栈,这里的数字不用真的计算,所以统一按字符处理
|
|
|
|
|
|
int main() {
|
|
|
cin >> s;
|
|
|
//遍历中缀表达式的每一个字符
|
|
|
for (int i = 0; i < s.size(); i++) {
|
|
|
//①如果当前位置是数字,读完所有连续数字,记录到后缀表达式中
|
|
|
if (isdigit(s[i])) {
|
|
|
//读出完整的数字
|
|
|
int x = 0;
|
|
|
while (i < s.size() && isdigit(s[i])) {
|
|
|
x = x * 10 + s[i] - '0';
|
|
|
i++;
|
|
|
}
|
|
|
i--; //加多了一位,需要减去
|
|
|
|
|
|
//将完整数字存入结果串中
|
|
|
t.append(to_string(x)); //字符串增加到字符串,用append
|
|
|
t.push_back(' '); //字符增加到字符串,用push_back
|
|
|
}
|
|
|
//② 如果当前位置是字母,比如a,b,c,..
|
|
|
else if (isalpha(s[i])) {
|
|
|
t.push_back(s[i]);
|
|
|
t.push_back(' ');
|
|
|
}
|
|
|
//③ 如果是左括号,那么直接入栈
|
|
|
else if (s[i] == '(')
|
|
|
stk.push(s[i]);
|
|
|
//④ 如果是右括号,就在栈中不断弹出操作符和数字,直到栈顶是(为止
|
|
|
else if (s[i] == ')') {
|
|
|
while (stk.top() != '(') {
|
|
|
t.push_back(stk.top());
|
|
|
t.push_back(' ');
|
|
|
stk.pop();
|
|
|
}
|
|
|
//弹出左括号,但不输出
|
|
|
stk.pop();
|
|
|
}
|
|
|
//⑤栈顶元素的优先级大于等于当前的运算符,就将其输出
|
|
|
else {
|
|
|
while (stk.size() && h[s[i]] <= h[stk.top()]) {
|
|
|
t.push_back(stk.top());
|
|
|
t.push_back(' ');
|
|
|
stk.pop();
|
|
|
}
|
|
|
//⑥当前运算符入栈
|
|
|
stk.push(s[i]);
|
|
|
}
|
|
|
}
|
|
|
//⑦ 如果不为空,就把所有的元素全部弹出
|
|
|
while (stk.size()) {
|
|
|
t.push_back(stk.top());
|
|
|
t.push_back(' ');
|
|
|
stk.pop();
|
|
|
}
|
|
|
//输出后缀表达式
|
|
|
printf("%s", t.c_str());
|
|
|
return 0;
|
|
|
}
|
|
|
```
|
|
|
#### 2、中缀表达式转后缀表达式(四则运算+不用空格隔开)
|
|
|
|
|
|
```cpp {.line-numbers}
|
|
|
#include <bits/stdc++.h>
|
|
|
using namespace std;
|
|
|
|
|
|
//中缀表达式转后缀表达式
|
|
|
/*
|
|
|
测试用例1:
|
|
|
a+b*c+(d*e+f)*g
|
|
|
|
|
|
答案:
|
|
|
abc*+de*f+g*+
|
|
|
|
|
|
|
|
|
测试用例2:
|
|
|
(6+3*(7-4))-8/2
|
|
|
|
|
|
答案:
|
|
|
6 3 7 4 - * + 8 2 / -
|
|
|
|
|
|
测试用例3:
|
|
|
(24*(9+6/38-5)+4)
|
|
|
答案:
|
|
|
24 9 6 38 / + 5 - * 4 +
|
|
|
*/
|
|
|
unordered_map<char, int> h{{'+', 1}, {'-', 1}, {'*', 2}, {'/', 2}};
|
|
|
string s;
|
|
|
string t;
|
|
|
stack<char> stk;
|
|
|
|
|
|
int main() {
|
|
|
cin >> s;
|
|
|
for (int i = 0; i < s.size(); i++) {
|
|
|
if (isdigit(s[i])) {
|
|
|
int x = 0;
|
|
|
while (i < s.size() && isdigit(s[i])) {
|
|
|
x = x * 10 + s[i] - '0';
|
|
|
i++;
|
|
|
}
|
|
|
i--;
|
|
|
t.append(to_string(x));
|
|
|
} else if (isalpha(s[i]))
|
|
|
t.push_back(s[i]);
|
|
|
else if (s[i] == '(')
|
|
|
stk.push(s[i]);
|
|
|
else if (s[i] == ')') {
|
|
|
while (stk.top() != '(') {
|
|
|
t.push_back(stk.top());
|
|
|
stk.pop();
|
|
|
}
|
|
|
stk.pop();
|
|
|
} else {
|
|
|
while (stk.size() && h[s[i]] <= h[stk.top()]) {
|
|
|
t.push_back(stk.top());
|
|
|
stk.pop();
|
|
|
}
|
|
|
stk.push(s[i]);
|
|
|
}
|
|
|
}
|
|
|
while (stk.size()) {
|
|
|
t.push_back(stk.top());
|
|
|
stk.pop();
|
|
|
}
|
|
|
printf("%s", t.c_str());
|
|
|
return 0;
|
|
|
}
|
|
|
```
|
|
|
#### 3、中缀表达式转后缀表达式(逻辑运算符+拷贝四则版本)
|
|
|
|
|
|
```cpp {.line-numbers}
|
|
|
#include <bits/stdc++.h>
|
|
|
using namespace std;
|
|
|
|
|
|
/*
|
|
|
中缀的逻辑表达式 转 后缀的逻辑表达式
|
|
|
|
|
|
测试用例:
|
|
|
0&(0|1|0)
|
|
|
|
|
|
答案:
|
|
|
001|0|&
|
|
|
*/
|
|
|
unordered_map<char, int> h{{'|', 1}, {'&', 2}};
|
|
|
string s;
|
|
|
string t;
|
|
|
stack<char> stk;
|
|
|
int main() {
|
|
|
cin >> s;
|
|
|
for (int i = 0; i < s.size(); i++) {
|
|
|
if (isdigit(s[i])) {
|
|
|
int x = 0;
|
|
|
while (i < s.size() && isdigit(s[i])) {
|
|
|
x = x * 10 + s[i] - '0';
|
|
|
i++;
|
|
|
}
|
|
|
i--;
|
|
|
t.append(to_string(x));
|
|
|
} else if (isalpha(s[i]))
|
|
|
t.push_back(s[i]);
|
|
|
else if (s[i] == '(')
|
|
|
stk.push(s[i]);
|
|
|
else if (s[i] == ')') {
|
|
|
while (stk.top() != '(') {
|
|
|
t.push_back(stk.top());
|
|
|
stk.pop();
|
|
|
}
|
|
|
stk.pop();
|
|
|
} else {
|
|
|
while (stk.size() && h[s[i]] <= h[stk.top()]) {
|
|
|
t.push_back(stk.top());
|
|
|
stk.pop();
|
|
|
}
|
|
|
stk.push(s[i]);
|
|
|
}
|
|
|
}
|
|
|
while (stk.size()) {
|
|
|
t.push_back(stk.top());
|
|
|
stk.pop();
|
|
|
}
|
|
|
printf("%s", t.c_str());
|
|
|
return 0;
|
|
|
}
|
|
|
```
|
|
|
#### 4、中缀表达式转后缀表达式(逻辑运算符+精简版本)
|
|
|
|
|
|
```cpp {.line-numbers}
|
|
|
#include <bits/stdc++.h>
|
|
|
using namespace std;
|
|
|
/*
|
|
|
中缀的逻辑表达式 转 后缀的逻辑表达式
|
|
|
|
|
|
测试用例:
|
|
|
0&(0|1|0)
|
|
|
|
|
|
答案:
|
|
|
001|0|&
|
|
|
*/
|
|
|
unordered_map<char, int> h{{'|', 1}, {'&', 2}};
|
|
|
string s;
|
|
|
string t;
|
|
|
stack<char> stk;
|
|
|
|
|
|
int main() {
|
|
|
cin >> s;
|
|
|
for (int i = 0; i < s.size(); i++) {
|
|
|
if (isdigit(s[i]) || isalpha(s[i]))
|
|
|
t.push_back(s[i]);
|
|
|
else if (s[i] == '(')
|
|
|
stk.push(s[i]);
|
|
|
else if (s[i] == ')') {
|
|
|
while (stk.top() != '(') {
|
|
|
t.push_back(stk.top());
|
|
|
stk.pop();
|
|
|
}
|
|
|
stk.pop();
|
|
|
} else {
|
|
|
while (stk.size() && h[s[i]] <= h[stk.top()]) {
|
|
|
t.push_back(stk.top());
|
|
|
stk.pop();
|
|
|
}
|
|
|
stk.push(s[i]);
|
|
|
}
|
|
|
}
|
|
|
while (stk.size()) {
|
|
|
t.push_back(stk.top());
|
|
|
stk.pop();
|
|
|
}
|
|
|
printf("%s", t.c_str());
|
|
|
return 0;
|
|
|
}
|
|
|
```
|
|
|
#### 5、中缀表达式求值(四则版本)
|
|
|
|
|
|
```cpp {.line-numbers}
|
|
|
// OJ 测试:
|
|
|
// AcWing 3302. 表达式求值
|
|
|
// https://www.acwing.com/problem/content/3305/
|
|
|
#include <bits/stdc++.h>
|
|
|
|
|
|
using namespace std;
|
|
|
/*
|
|
|
中缀表达式求值
|
|
|
|
|
|
测试用例I:
|
|
|
(2+2)*(1+1)
|
|
|
|
|
|
答案:8
|
|
|
|
|
|
测试用例II:
|
|
|
2+(3*4)-((5*9-5)/8-4)
|
|
|
|
|
|
答案:13
|
|
|
*/
|
|
|
|
|
|
stack<int> num; //数字栈
|
|
|
stack<char> op; //操作符栈
|
|
|
|
|
|
//优先级表
|
|
|
unordered_map<char, int> h{{'+', 1}, {'-', 1}, {'*', 2}, {'/', 2}};
|
|
|
|
|
|
/**
|
|
|
* 功能:计算两个数的和差积商
|
|
|
*/
|
|
|
void eval() {
|
|
|
int a = num.top(); //第二个操作数
|
|
|
num.pop();
|
|
|
|
|
|
int b = num.top(); //第一个操作数
|
|
|
num.pop();
|
|
|
|
|
|
char p = op.top(); //运算符
|
|
|
op.pop();
|
|
|
|
|
|
int r; //结果
|
|
|
//计算结果
|
|
|
if (p == '+')
|
|
|
r = b + a;
|
|
|
else if (p == '-')
|
|
|
r = b - a;
|
|
|
else if (p == '*')
|
|
|
r = b * a;
|
|
|
else if (p == '/')
|
|
|
r = b / a;
|
|
|
//结果入栈
|
|
|
num.push(r);
|
|
|
}
|
|
|
|
|
|
int main() {
|
|
|
//读入表达式
|
|
|
string s;
|
|
|
cin >> s;
|
|
|
//遍历字符串的每一位
|
|
|
for (int i = 0; i < s.size(); i++) {
|
|
|
//① 如果是数字,则入栈
|
|
|
if (isdigit(s[i])) {
|
|
|
//读出完整的数字
|
|
|
int x = 0;
|
|
|
while (i < s.size() && isdigit(s[i])) {
|
|
|
x = x * 10 + s[i] - '0';
|
|
|
i++;
|
|
|
}
|
|
|
i--; //加多了一位,需要减去
|
|
|
|
|
|
num.push(x); //数字入栈
|
|
|
}
|
|
|
//② 左括号无优先级,入栈
|
|
|
else if (s[i] == '(')
|
|
|
op.push(s[i]);
|
|
|
//③ 右括号时,需计算最近一对括号里面的值
|
|
|
else if (s[i] == ')') {
|
|
|
//从栈中向前找,一直找到左括号
|
|
|
while (op.top() != '(') eval(); //将左右括号之间的计算完,维护回栈里
|
|
|
//左括号出栈
|
|
|
op.pop();
|
|
|
} else { //④ 运算符
|
|
|
//如果待入栈运算符优先级低,则先计算
|
|
|
while (op.size() && h[op.top()] >= h[s[i]]) eval();
|
|
|
op.push(s[i]); //操作符入栈
|
|
|
}
|
|
|
}
|
|
|
while (op.size()) eval(); //⑤ 剩余的进行计算
|
|
|
printf("%d\n", num.top()); //输出结果
|
|
|
return 0;
|
|
|
}
|
|
|
|
|
|
```
|
|
|
#### 6、中缀表达式求值(逻辑表达式+拷贝四则版本)
|
|
|
|
|
|
```cpp {.line-numbers}
|
|
|
#include <bits/stdc++.h>
|
|
|
using namespace std;
|
|
|
|
|
|
/*
|
|
|
0&(1|0)|(1|1|1&0)
|
|
|
答案:1
|
|
|
|
|
|
(0|1&0|1|1|(1|1))&(0&1&(1|0)|0|1|0)&0
|
|
|
答案:0
|
|
|
*/
|
|
|
unordered_map<char, int> h{{'|', 1}, {'&', 2}};
|
|
|
stack<int> num;
|
|
|
stack<char> op;
|
|
|
|
|
|
void eval() {
|
|
|
int a = num.top();
|
|
|
num.pop();
|
|
|
|
|
|
int b = num.top();
|
|
|
num.pop();
|
|
|
|
|
|
char p = op.top();
|
|
|
op.pop();
|
|
|
|
|
|
int r;
|
|
|
if (p == '|')
|
|
|
r = b | a;
|
|
|
else if (p == '&')
|
|
|
r = b & a;
|
|
|
num.push(r);
|
|
|
}
|
|
|
|
|
|
int main() {
|
|
|
string s;
|
|
|
cin >> s;
|
|
|
for (int i = 0; i < s.size(); i++) {
|
|
|
if (isdigit(s[i])) {
|
|
|
int x = 0;
|
|
|
while (i < s.size() && isdigit(s[i])) {
|
|
|
x = x * 10 + s[i] - '0';
|
|
|
i++;
|
|
|
}
|
|
|
i--;
|
|
|
|
|
|
num.push(x);
|
|
|
} else if (s[i] == '(')
|
|
|
op.push(s[i]);
|
|
|
else if (s[i] == ')') {
|
|
|
while (op.top() != '(') eval();
|
|
|
op.pop();
|
|
|
} else {
|
|
|
while (op.size() && h[op.top()] >= h[s[i]]) eval();
|
|
|
op.push(s[i]);
|
|
|
}
|
|
|
}
|
|
|
while (op.size()) eval();
|
|
|
|
|
|
printf("%d\n", num.top());
|
|
|
return 0;
|
|
|
}
|
|
|
|
|
|
```
|
|
|
#### 7、中缀表达式求值(逻辑表达式+简化版本)
|
|
|
|
|
|
```cpp {.line-numbers}
|
|
|
#include <bits/stdc++.h>
|
|
|
using namespace std;
|
|
|
|
|
|
/*
|
|
|
0&(1|0)|(1|1|1&0)
|
|
|
答案:1
|
|
|
|
|
|
(0|1&0|1|1|(1|1))&(0&1&(1|0)|0|1|0)&0
|
|
|
答案:0
|
|
|
*/
|
|
|
unordered_map<char, int> h{{'|', 1}, {'&', 2}};
|
|
|
stack<int> num;
|
|
|
stack<char> op;
|
|
|
|
|
|
void eval() {
|
|
|
int a = num.top();
|
|
|
num.pop();
|
|
|
|
|
|
int b = num.top();
|
|
|
num.pop();
|
|
|
|
|
|
char p = op.top();
|
|
|
op.pop();
|
|
|
|
|
|
int r;
|
|
|
if (p == '|')
|
|
|
r = b | a;
|
|
|
else if (p == '&')
|
|
|
r = b & a;
|
|
|
num.push(r);
|
|
|
}
|
|
|
|
|
|
int main() {
|
|
|
string s;
|
|
|
cin >> s;
|
|
|
for (int i = 0; i < s.size(); i++) {
|
|
|
if (isdigit(s[i]))
|
|
|
num.push(s[i] - '0');
|
|
|
else if (s[i] == '(')
|
|
|
op.push(s[i]);
|
|
|
else if (s[i] == ')') {
|
|
|
while (op.top() != '(') eval();
|
|
|
op.pop();
|
|
|
} else {
|
|
|
while (op.size() && h[op.top()] >= h[s[i]]) eval();
|
|
|
op.push(s[i]);
|
|
|
}
|
|
|
}
|
|
|
while (op.size()) eval();
|
|
|
|
|
|
printf("%d\n", num.top());
|
|
|
return 0;
|
|
|
}
|
|
|
|
|
|
```
|
|
|
|
|
|
铺垫的知识完成,现在开始分析本题:
|
|
|
|
|
|
* 中缀逻辑表达式求值
|
|
|
* 记录短路次数
|
|
|
|
|
|
#### 规律总结
|
|
|
用一个三元组来替换原版本放在栈里的$int$,即:
|
|
|
$Node(v,a,b)$,代表:当前数字值是$v$,已经计算过的$\&$短路次数是$a$,已经计算过的$|$短路次数是$b$
|
|
|
|
|
|
找一个思路相似的简单问题给大家看看:
|
|
|

|
|
|
|
|
|
则有下面的递推式:
|
|
|
$\large (1,a_1,b_1) | (?,a_2,b_2) \Rightarrow (1,a_1,b_1+1) 发生了短路运算,后面的不再计算$
|
|
|
$\large (0,a_1,b_1) | (?,a_2,b_2) \Rightarrow (?,a_1+a_2,b_1+b_2) 没有发生短路计算$
|
|
|
$\large (1,a_1,b_1) \& (?,a_2,b_2) \Rightarrow (?,a_1+a_2,b_1+b_2) 没有发生短路计算$
|
|
|
$\large (0,a_1,b_1) \& (?,a_2,b_2) \Rightarrow (0,a_1+1,b_1) 发生了短路运算,后面的不再计算$
|
|
|
|
|
|
实现代码:
|
|
|
|
|
|
```cpp {.line-numbers}
|
|
|
#include <bits/stdc++.h>
|
|
|
using namespace std;
|
|
|
|
|
|
struct Node {
|
|
|
int v, a, b; // v:代表当前的结果值,a: &短路的次数 b:|短路的次数
|
|
|
};
|
|
|
|
|
|
stack<Node> num;
|
|
|
stack<char> op;
|
|
|
|
|
|
/*
|
|
|
测试用例1:
|
|
|
0&(1|0)|(1|1|1&0)
|
|
|
答案:
|
|
|
1
|
|
|
1 2
|
|
|
|
|
|
测试用例2:
|
|
|
(0|1&0|1|1|(1|1))&(0&1&(1|0)|0|1|0)&0
|
|
|
答案:
|
|
|
0
|
|
|
2 3
|
|
|
*/
|
|
|
unordered_map<char, int> h{{'|', 1}, {'&', 2}, {'(', 0}};
|
|
|
|
|
|
void eval() {
|
|
|
//这里要注意从栈中弹出元素的顺序,先出来的是y,后出来的是x
|
|
|
Node y = num.top();
|
|
|
num.pop();
|
|
|
|
|
|
Node x = num.top();
|
|
|
num.pop();
|
|
|
|
|
|
char p = op.top();
|
|
|
op.pop();
|
|
|
|
|
|
Node r;
|
|
|
if (p == '|') {
|
|
|
if (x.v == 1)
|
|
|
r = {1, x.a, x.b + 1};
|
|
|
else
|
|
|
r = {y.v, x.a + y.a, x.b + y.b};
|
|
|
} else if (p == '&') {
|
|
|
if (x.v == 1)
|
|
|
r = {y.v, x.a + y.a, x.b + y.b};
|
|
|
else
|
|
|
r = {0, x.a + 1, x.b};
|
|
|
}
|
|
|
num.push(r);
|
|
|
}
|
|
|
|
|
|
int main() {
|
|
|
string s;
|
|
|
cin >> s;
|
|
|
for (int i = 0; i < s.size(); i++) {
|
|
|
if (isdigit(s[i])) {
|
|
|
int x = 0;
|
|
|
while (i < s.size() && isdigit(s[i])) {
|
|
|
x = x * 10 + s[i] - '0';
|
|
|
i++;
|
|
|
}
|
|
|
i--;
|
|
|
num.push({x, 0, 0});
|
|
|
} else if (s[i] == '(')
|
|
|
op.push(s[i]);
|
|
|
else if (s[i] == ')') {
|
|
|
while (op.top() != '(') eval();
|
|
|
op.pop();
|
|
|
} else {
|
|
|
while (op.size() && h[op.top()] >= h[s[i]]) eval();
|
|
|
op.push(s[i]);
|
|
|
}
|
|
|
}
|
|
|
while (op.size()) eval();
|
|
|
|
|
|
printf("%d\n", num.top().v);
|
|
|
printf("%d %d\n", num.top().a, num.top().b);
|
|
|
return 0;
|
|
|
}
|
|
|
```
|
|
|
|
|
|
|
|
|
|
|
|
### [$CSP-J$ $2022$] 上升点列
|
|
|
[P8816 [CSP-J 2022] 上升点列(民间数据)](https://www.luogu.com.cn/problem/P8816)
|
|
|
|
|
|
[前导知识练习 力扣 664. 奇怪的打印机](https://www.cnblogs.com/littlehb/p/16869777.html)
|
|
|
|
|
|
|
|
|
样例$1$输入解析
|
|
|
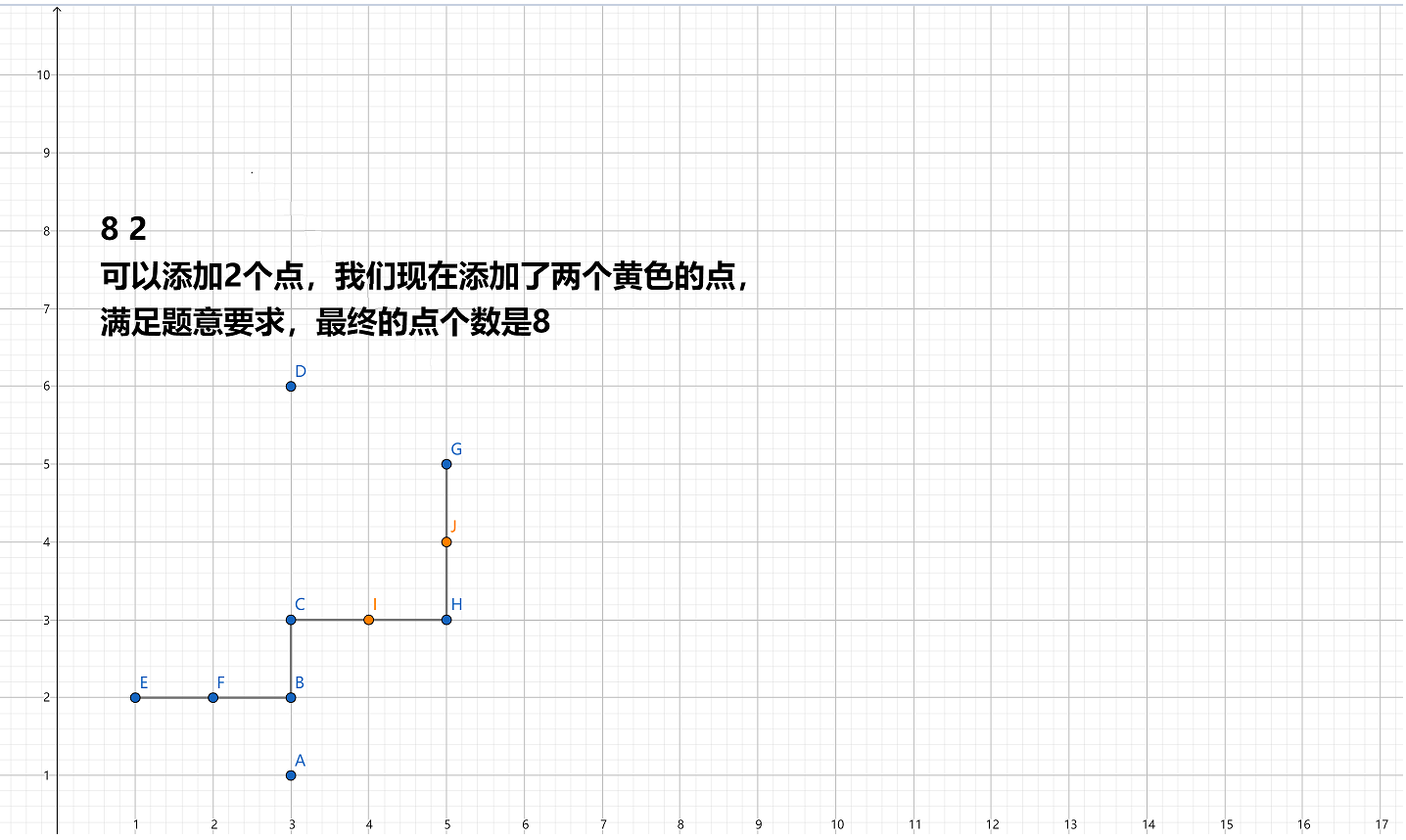
|
|
|
|
|
|
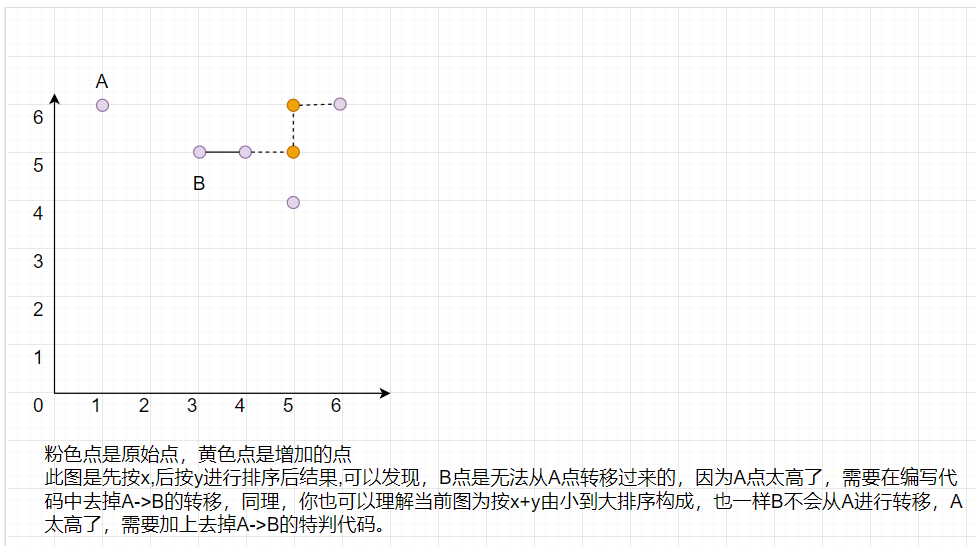
|
|
|
|
|
|
#### 动态规划解法
|
|
|
|
|
|
这种题目乍一看就能想到是 **$dp$** 或者 **二分**,从哪个先开始考虑都没问题
|
|
|
|
|
|
思考二分最后会发现不知道该从何入手,如果是二分长度,那不知道起点,二分起点,那也没有意义
|
|
|
|
|
|
再配合数据范围只有$500$,这种数据范围大概率就是$dp$,那么来思考$dp$
|
|
|
|
|
|
#### 状态表示
|
|
|
很容易想到$f[i][j]$表示到第$i$个节点,已经用掉了$j$个可添加点的 **最大长度**
|
|
|
|
|
|
#### 状态转移
|
|
|
状态有了,转移应该也很容易想到,对于第$i$个节点,无非就是枚举其他节点$j$,如果$j$在$i$的左下方即可进行转移,计算
|
|
|
$$\large d=a[i].x-a[j].x+a[i].y-a[j].y-1$$
|
|
|
即$j$到$i$ 需要使用 $d$ 个可添加点
|
|
|
|
|
|
现在的场景是从$j->i$,对于状态表示$f[i][?]$的一维已经确定是从$f[j][?]->f[i][??]$了,这两个问题间的转移是关键问题了:
|
|
|
|
|
|
那么枚举$f[j][k]$,即可得到方程
|
|
|
$$\large f[i][k+d]=max(f[j][k]+d+1)$$
|
|
|
|
|
|
最后答案即为
|
|
|
$$\large ans = max(ans, f[i][k + d] + m - k - d)$$
|
|
|
|
|
|
#### 注意
|
|
|
这里注意一个小细节,如果总共有 $m$ 个可添加点,只用了$k+d$个,多出来的$m-k-d$个直接加在最后即可,不要忘记这个,不过这个坑在第二组$sample$里就给出来了,基本不会有人踩
|
|
|
|
|
|
<font color='red' size=4><b>不把测试用例看完,画出来,理解掉的人是傻子!!!</b></font>
|
|
|
|
|
|
检查一下复杂度,是$O(n^2K)$,显然没有问题
|
|
|
```cpp {.line-numbers}
|
|
|
#include <bits/stdc++.h>
|
|
|
using namespace std;
|
|
|
const int N = 510;
|
|
|
const int M = 110;
|
|
|
struct Node {
|
|
|
int x, y;
|
|
|
/*
|
|
|
Q1:为什么要排序?
|
|
|
A:因为要DP,需要解决无后效性。也就是有一定的单调性,从左向右,从上向下填表,填完的数值不能再被修改,需要有一定的依赖关系顺序
|
|
|
|
|
|
Q2:按什么来排序?
|
|
|
A:可以按x+y来排序,也可以按先x,后y的方式来排序,都是一样的。
|
|
|
|
|
|
1.按x+y排序
|
|
|
const bool operator<(const Node &t) {
|
|
|
return x + y < t.x + t.y;
|
|
|
}
|
|
|
*/
|
|
|
// 2.先按x,再按y排序
|
|
|
const bool operator<(const Node &t) {
|
|
|
if (x == t.x) return y < t.y;
|
|
|
return x < t.x;
|
|
|
}
|
|
|
} a[N];
|
|
|
|
|
|
int f[N][M];
|
|
|
int ans;
|
|
|
|
|
|
int main() {
|
|
|
//文件输入
|
|
|
// freopen("point.in", "r", stdin);
|
|
|
|
|
|
int n, m;
|
|
|
cin >> n >> m;
|
|
|
|
|
|
for (int i = 1; i <= n; ++i) cin >> a[i].x >> a[i].y;
|
|
|
sort(a + 1, a + 1 + n);
|
|
|
|
|
|
// dp初始化,最后一个点是以i号点选中,并且,使用了j个虚拟点情况下,获得的最长序列长度
|
|
|
for (int i = 1; i <= n; i++)
|
|
|
for (int j = 0; j <= m; j++)
|
|
|
f[i][j] = j + 1; //以i点结束,并且,使用了j个虚拟点,最起码可以构成一个最长长度为j+1的序列
|
|
|
|
|
|
//状态转移
|
|
|
for (int i = 1; i <= n; i++) //枚举每个原始点
|
|
|
for (int j = 1; j < i; j++) { //枚举每个前序点
|
|
|
if (a[i].x < a[j].x || a[i].y < a[j].y) continue; //如果j不在i的左下方,无效转移
|
|
|
int d = a[i].x - a[j].x + a[i].y - a[j].y - 1; // j->i 需要增加的虚拟点个数
|
|
|
|
|
|
/*
|
|
|
讨论j点的哪些子状态 可以转移到 i的哪些子状态?
|
|
|
思考一下f[j]的二维状态,最小值是0,最大值是m
|
|
|
现在f[j]的二维状态变化量是固定的,是d
|
|
|
所以需要枚举j的所有以转移的二维状态值:0 ~ m-d
|
|
|
*/
|
|
|
for (int k = 0; k <= m - d; k++) {
|
|
|
// f[j][k]是前序状态,可以通过+d转移到新的状态
|
|
|
// f[j][k+d]+d+1 -> f[i][k+d]
|
|
|
f[i][k + d] = max(f[i][k + d], f[j][k] + d + 1);
|
|
|
|
|
|
//在状态转移完成后,收集一下答案
|
|
|
//小坑一个:给你m个虚拟点,你最后没用了的话,就是浪费,因为最起码,
|
|
|
//把多出来的放在最后就可以增长序列长度
|
|
|
ans = max(ans, f[i][k + d] + m - k - d); //更新序列最长长度
|
|
|
}
|
|
|
}
|
|
|
|
|
|
//输出结果
|
|
|
printf("%d\n", ans);
|
|
|
return 0;
|
|
|
}
|
|
|
```
|
|
|
|
|
|
[最优子结构及 $dp$ 数组遍历方向的问题](https://zhuanlan.zhihu.com/p/100993613)
|
|
|
|
|
|
* $1$、遍历的过程中,所需的状态必须是已经计算出来的
|
|
|
* $2$、遍历的终点必须是存储结果的那个位置
|
|
|
|
|
|
#### 记忆化搜索解法I
|
|
|
```c++
|
|
|
#include <bits/stdc++.h>
|
|
|
const int N = 510;
|
|
|
|
|
|
//性能:第12号测试点,时间最长,65ms
|
|
|
|
|
|
/*
|
|
|
搜索代码:暴力枚举每次选择哪个点,能选就选,维护剩下几个自由点,加个记忆化即可通过
|
|
|
*/
|
|
|
using namespace std;
|
|
|
int n, m, ans;
|
|
|
int x[N], y[N]; //对于二维坐标,两个x,y数组,明显比使用struct的结构体数组方便,但是,不利用整体排序
|
|
|
int f[N][N]; //结果数组
|
|
|
|
|
|
//从u点出发,还有r个虚拟点可用,可以获得的最长序列长度是多少
|
|
|
int dfs(int u, int r) {
|
|
|
if (~f[u][r]) return f[u][r]; //计算过则直接返回
|
|
|
int ans = r + 1; //剩余r个虚拟点,再加上当前点u,最起码能有r+1点的序列长度
|
|
|
|
|
|
for (int i = 1; i <= n; i++) { //谁能做为我的后续点
|
|
|
if (u == i) continue; //自己不能做为自己的直接后续点
|
|
|
if (x[i] < x[u] || y[i] < y[u]) continue; //排除掉肯定不可能成为我后续点的点
|
|
|
int d = x[i] - x[u] + y[i] - y[u] - 1; // u->i之间缺少 多少个虚拟点
|
|
|
if (d > r) continue; //如果需要的虚拟点个数大于剩余的虚拟点个数,那么i 无法做为u的后续点
|
|
|
ans = max(ans, dfs(i, r - d) + d + 1); //在消耗了d个虚拟点之后,成功到达了i这个点;
|
|
|
//①已经取得的序列长度贡献u和d个虚拟点,共d+1个
|
|
|
//②问题转化为求未知部分:以i点为出发点,剩余虚拟点个数r-d个的情况下可以获取到的最长序列长度
|
|
|
}
|
|
|
return f[u][r] = ans; //记忆化
|
|
|
}
|
|
|
|
|
|
int main() {
|
|
|
//文件输入
|
|
|
// freopen("point.in", "r", stdin);
|
|
|
memset(f, -1, sizeof f);
|
|
|
|
|
|
cin >> n >> m;
|
|
|
for (int i = 1; i <= n; i++) cin >> x[i] >> y[i];
|
|
|
|
|
|
for (int i = 1; i <= n; i++) ans = max(ans, dfs(i, m));
|
|
|
printf("%d\n", ans);
|
|
|
return 0;
|
|
|
}
|
|
|
```
|
|
|
|
|
|
#### 记忆化搜索优化版本
|
|
|
```c++
|
|
|
#include <bits/stdc++.h>
|
|
|
const int N = 510;
|
|
|
|
|
|
//性能:第12号测试点,时间最长,22ms
|
|
|
/*
|
|
|
搜索代码:暴力枚举每次选择哪个点,能选就选,维护剩下几个自由点,加个记忆化即可通过
|
|
|
*/
|
|
|
using namespace std;
|
|
|
int n, m, ans;
|
|
|
|
|
|
int f[N][N]; //结果数组
|
|
|
struct Node {
|
|
|
int x, y;
|
|
|
const bool operator<(Node &t) const {
|
|
|
if (x == t.x) return y < t.y;
|
|
|
return x < t.x;
|
|
|
}
|
|
|
} a[N];
|
|
|
|
|
|
//从u点出发,还有r个虚拟点可用,可以获得的最长序列长度是多少
|
|
|
int dfs(int u, int r) {
|
|
|
if (~f[u][r]) return f[u][r]; //计算过则直接返回
|
|
|
int ans = r + 1; //剩余r个虚拟点,再加上当前点u,最起码能有r+1点的序列长度
|
|
|
|
|
|
for (int i = u + 1; i <= n; i++) { //谁能做为我的后续点
|
|
|
if (u == i) continue; //自己不能做为自己的直接后续点
|
|
|
if (a[i].x < a[u].x || a[i].y < a[u].y) continue; //排除掉肯定不可能成为我后续点的点
|
|
|
int d = a[i].x - a[u].x + a[i].y - a[u].y - 1; // u->i之间缺少 多少个虚拟点
|
|
|
if (d > r) continue; //如果需要的虚拟点个数大于剩余的虚拟点个数,那么i 无法做为u的后续点
|
|
|
ans = max(ans, dfs(i, r - d) + d + 1); //在消耗了d个虚拟点之后,成功到达了i这个点;
|
|
|
//①已经取得的序列长度贡献u和d个虚拟点,共d+1个
|
|
|
//②问题转化为求未知部分:以i点为出发点,剩余虚拟点个数r-d个的情况下可以获取到的最长序列长度
|
|
|
}
|
|
|
return f[u][r] = ans; //记忆化
|
|
|
}
|
|
|
|
|
|
int main() {
|
|
|
//文件输入
|
|
|
// freopen("point.in", "r", stdin);
|
|
|
|
|
|
memset(f, -1, sizeof f);
|
|
|
|
|
|
cin >> n >> m;
|
|
|
for (int i = 1; i <= n; i++) cin >> a[i].x >> a[i].y;
|
|
|
sort(a + 1, a + 1 + n);
|
|
|
|
|
|
for (int i = 1; i <= n; i++) ans = max(ans, dfs(i, m));
|
|
|
printf("%d\n", ans);
|
|
|
return 0;
|
|
|
}
|
|
|
``` |