huanghai
/
python
1
0
Fork 0
Code Issues Pull Requests Packages Projects Releases Wiki Activity
You can not select more than 25 topics Topics must start with a letter or number, can include dashes ('-') and can be up to 35 characters long.
Branches Tags
${ item.name }
Create tag ${ searchTerm }
Create branch ${ searchTerm }
from 'b7c3f8675f'
${ noResults }
python/TangDou/CSP-J/J1_2022/CSP-J2022.md

18 KiB
Raw Blame History Escape

This file contains invisible Unicode characters!

This file contains invisible Unicode characters that may be processed differently from what appears below. If your use case is intentional and legitimate, you can safely ignore this warning. Use the Escape button to reveal hidden characters.

This file contains ambiguous Unicode characters that may be confused with others in your current locale. If your use case is intentional and legitimate, you can safely ignore this warning. Use the Escape button to highlight these characters.

2022 CCF 非专业级别软件能力认证第一轮　试题解析

零一原创：2022CSP-J初赛真题答案及全面讲解

数学编程罗老师 CSP-j2022 CSP-J 2022 入门级 第一轮 阅读程序（2） 第22-27题

一、单项选择题

1、C++语言的面向对象特性：

A、C++中调用printf函数 printf函数在C语言中就存在，用来进行输出。在C++中，输入和输出增加了cin,cout。而C语言不是面向对象的，所以，printf与面向对象无关。此题答案选择A。

所谓面向对象，是指针对某些事物进行抽象，归纳为同一类物品，具有共同的属性，比如：鸟类包括麻雀，丹顶鹤，鹦鹉等，共同属性是有翅膀，孵蛋等。B,C,D都提到了类字样或"Class,Struct"等，这均是明显的面向对象概念。

2、非法出栈顺序

办法：出栈的顺序并不唯一，只能是一个个选项进行判断： 入栈顺序　6　5　4　3　2　1

A、5　4　3　6　1　2 6入，5入，此时5出，则栈中只有6 4入，4出，则栈中只有6 3入，3出，则栈中只有6 2 入栈，栈中 6　2 2出栈，剩6 1入栈，剩6　1 1出栈，剩6 6出栈，栈空　OK,A没有问题。

B. 4　5　3　1　2　6 6　5　4 入栈，4出栈，栈中剩 6　5 5出栈，栈中剩6 3入栈，3出栈，栈中剩6 2入栈，1入栈，此时1出栈，则栈中剩6　2 2出栈，剩6 6出栈，栈空，OK，B没有问题。

C、3　4　6　5　2　1 　6　5　4　3入栈，3出栈，栈中剩 6　5　4 4出栈，栈中剩6　5，此时要求6出栈，作不到，C错误！

D、2　3　4　1　5　6 为了2能先出栈，必须先入栈，则 6　5　4　3　2入栈 2　3　4　出栈 剩 6　5 1入栈　剩　6　5　1 1　5　6出栈，OK，没有问题，答案选C

3、 如图理解，答案:D

20221030110833

4、链表和数组的区别

定义

数组：一组具有相同数据类型的变量的集合。

链表：一种物理存储单元上非连续、非顺序的存储结构，数据元素的逻辑顺序是通过链表中的指针链接次序实现的。

区别

逻辑结构： （1）数组在内存中连续；链表采用动态内存分配的方式，在内存中不连续。 （2）数组在使用前事先固定长度，不能改变数组长度；链表支持动态增删元素。 （3）数组元素减少时会造成内存浪费；链表可以使用malloc或new来申请内存，不用时使用free或delete来释放内存。

内存结构： 数组从栈上分配内存，使用方便但自由度小；链表在堆上分配内存，自由度大但要注意造成内存泄漏。

访问效率： 数组在内存中顺序存储，通过下标访问，访问效率高；链表需要从头遍历访问，访问效率低。

越界问题： 数组大小固定，存在访问越界的风险；链表只要能申请空间就无越界风险。

A、数组不能排序，链表可以 　很明显，说反了，数组可以进行排序，反倒是链接不能排序

B、链表比数组能存储更多的信息 这个不一定，数组也能保存很多信息，只要你开的数组够大

C、数组大小固定，链表大小可动态调整 　这个完全正确，当然，这里说的数组是指static数组，不是指vector

D、以上均正确，这个无疑可以排除掉，因为最起码A是错的。

5、此题与上面第二题其实本质上是一样的，我们来模拟分析一下：

为了e2先出队列，必须它先入栈，即入栈应该是 e1,e2 此时栈中 e1,e2 e2出栈，入队列，出队列，栈内e1 e4想要出队列，需要e4出栈，则e3,e4入栈，栈内e1,e3,e4 e4出栈后，栈内e1,e3 e3出栈，e3入队列，e3出队列,栈内e1 e6想出队列，必须先入栈，则e1,e5,e6 e6出队列，e5出队列，e1出队列，栈空

回头看下，栈内最长长度为3，选择B

6、对表达式a+(b-c)*d的前缀表达式为( ),其中+,-,*,/是运算符。

  • b-c 先来，-bc
  • 乘法随后 *-bcd
  • 最后是加法+a*-bcd 答案是B

详细的解析见博文22张图带你深入剖析前缀、中缀、后缀表达式以及表达式求值

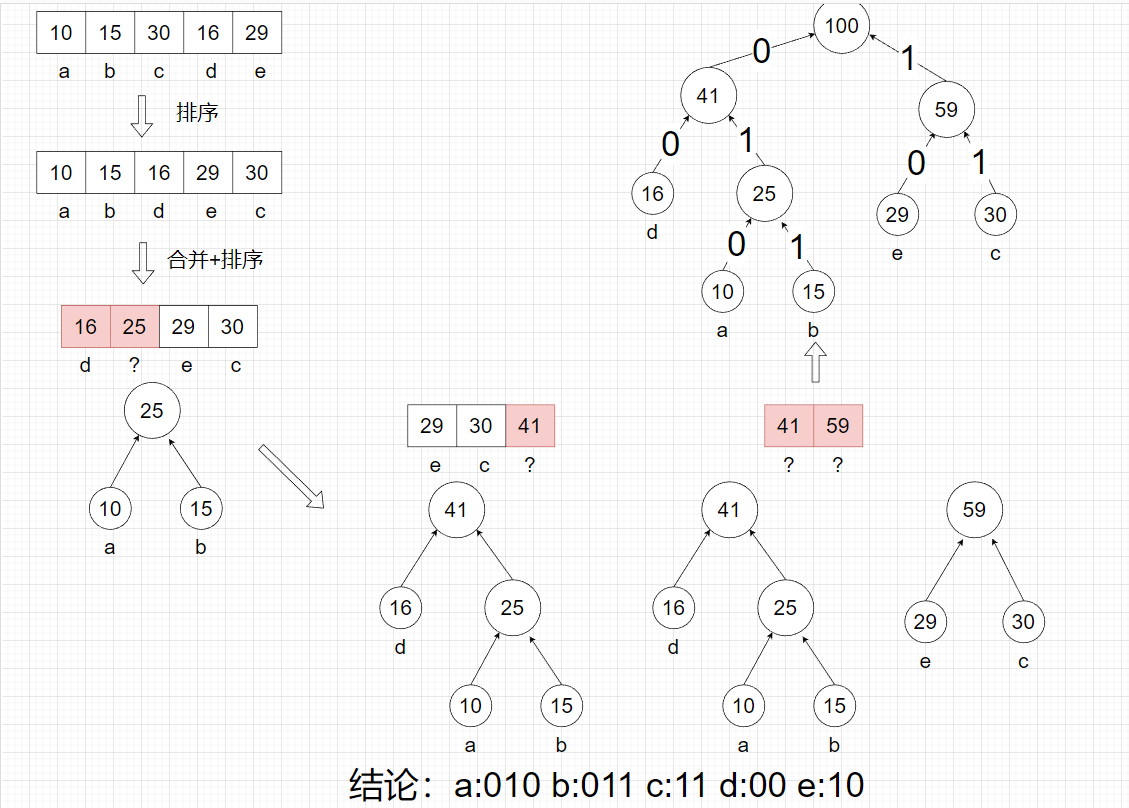
7、哈夫曼编码

哈夫曼编码（Huffman Coding）原理详解

其它博文讲解

哈夫曼编码（Huffman Coding）多图详细解析

a b c d e
10 15 30 16 29

####　1、按哈夫曼的思路排序:

a b d e c
10 15 16 29 30

2、构建哈夫曼树

答案：B

8、完全二叉树

解释I

解释II

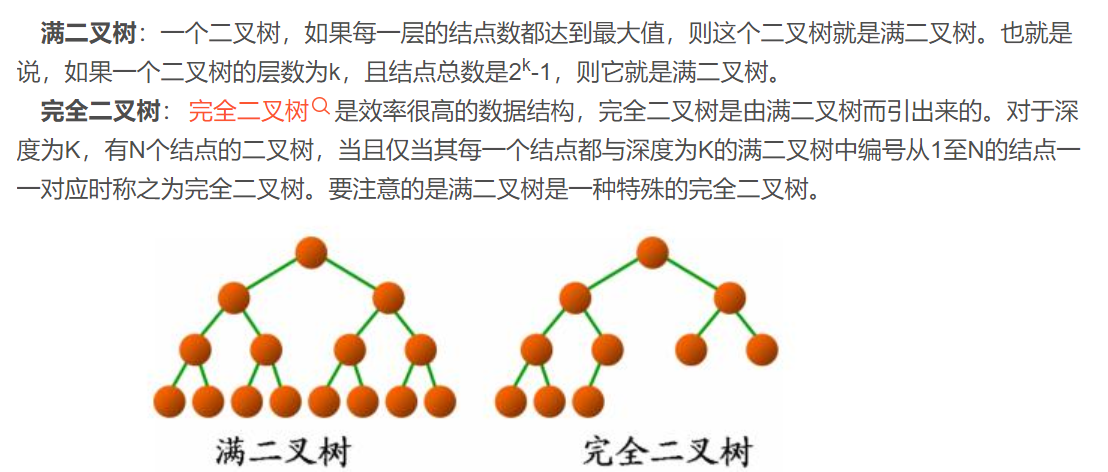
此题选:C

9、有向连通图+邻接矩阵存储

  • 有向，邻接矩阵记录的是每条有向边　
  • 连通图，最简单的连通图是一个链，即N-1条边，使用邻接矩阵记录的话，就是N个点

所以非零元素最少是N个，选择B

10、对数据结构表述不恰当的是：

  • 图的深度优先遍历遍历算法常使用的数据结构为栈。 dfs本质是递归，使用的数据结构是栈，此说法正确。

  • 栈的访问原则为后进先出，队列的访问原则是先进先出 这种说法是正确的，有时也说栈是先进后出

  • 队列常常被用于广度优先搜索算法 正确

  • 栈与队列存在本质不同，无法用栈实现队列 此说法不正确，用两个栈可以模拟出一个队列。

用两个栈实现一个队列&用两个队列实现一个栈

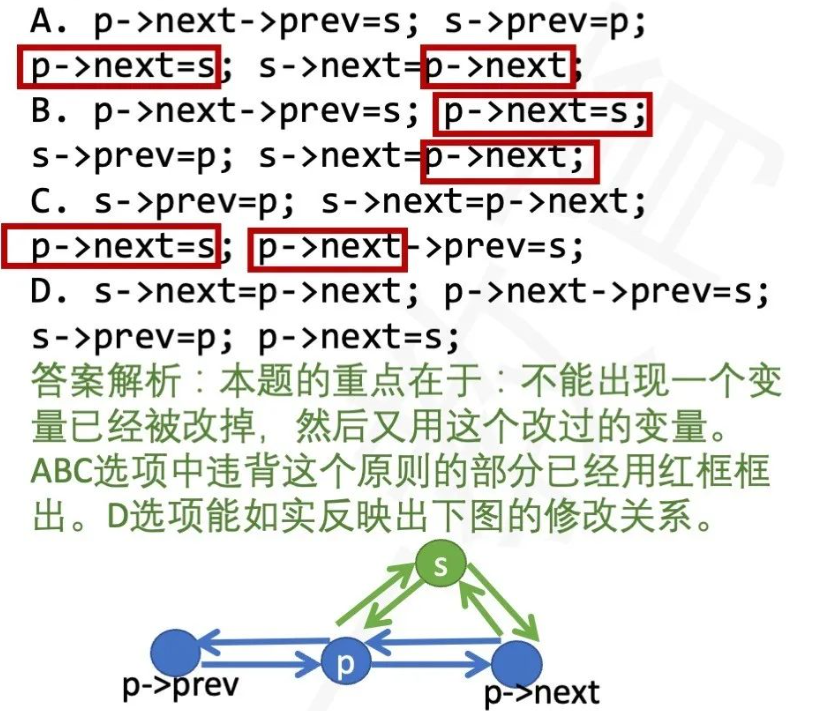
11、哪种操作顺序上正确的:

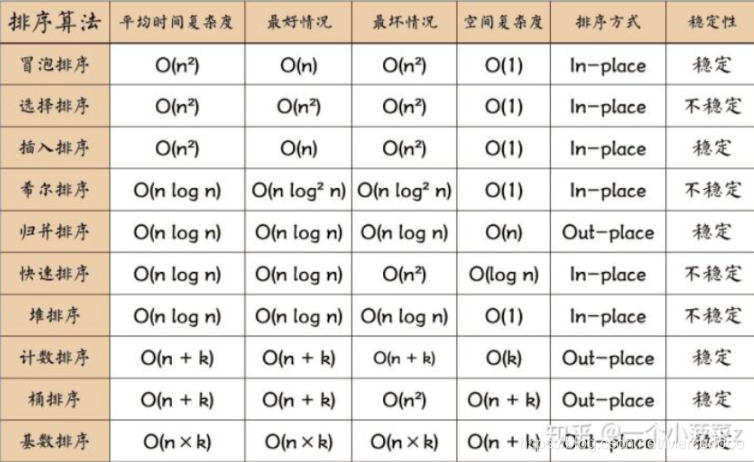
12、以下排序算法的常见实现中，哪个选项的说法是错误的：

A、冒泡排序算法是稳定的

B、简单选择排序是稳定的

C、简单插入排序是稳定的

D、归并排序算法是稳定的

算法
稳定 冒泡排序、插入排序、归并排序、基数排序
不稳定 堆排序、快速排序、希尔排序、选择排序

答案：B

冒泡排序

选择排序

插入法

归并排序

Q: 什么是排序算法的稳定性？

排序前后两个相等的数相对位置不变，则算法稳定

Q: 为什么选择排序不稳定呢？

答：假设有一个待排序的序列： 2 3 2 1 4 我们知道第一趟排序后就会选择第1个元素2和元素1交换，那么原来序列中两个2的相对顺序就被破坏了，所以选择排序是 不稳定 的排序算法。

排序的稳定性

不稳定：快选堆希

各种排序算法稳定性分析

13、八进制数32.1对应的十进制数是（）

A. 24.125 B. 24.250 C. 26.125 D. 26.250

32=2*8^0+3*8^1=2+24=26 ,所以排除A,B 小数部分 0.1=1*8^{-1}=1/8=0.125 答案选择C

14、互不相同的子串

abcab

一个：a,b,c 共3个 两个：ab,bc,ca 三个：abc,bca,cab 四个：abca,bcab 五个：abcab

共12个，答案：A

####　15、递归描述正确的：B

阅读程序类试题的方法论

  1. 举栗子模拟，一般采用不大不小的数字，如果有多个参数，尽量别设置一样的大小，比如n=4,m=5
  2. 用人脑模拟电脑进行运行，以纸笔形式记录计算结果
  3. 数形结合画成图，以图形式方式方便理解
  4. 阅读程序愿意考查递归或动态规划问题，对于递归问题可能着重考查重复计算次数等，要把这一块的知识彻底搞清楚
  5. 推导计算要由边界开始，比如一行一列，二行一列，....，不要上来就想通用形式。
  6. 有送分题，可以注意边界情况
  7. 有的时候要靠心算的，对心智要求挺高
  8. 有些数不好算，时间还长的，可以考虑蒙一个答案，不要期望答100分
  9. 平时多阅读一些有关的信息学奥赛常见问题，比如：约瑟夫圆环，高空扔鸡蛋等，有原型再思考就心里更有底。
  10. 根据前面推出的一些数据，来找规律，推测后面的数据。

二、阅读程序

20220921150052

十六进制与二进制转换

再来研究一下0x33,0x55: 这样写是16进制的意思，可以理解为:

  • 0x33=3*16^0+3*16^1=3+38=51
  • 0x55=5*16^0+5*16^1=5+80=85 但是，如果我们真的把它转为十进制，再转成二进制进行位运算，可就真的是南辕北辙了：

十六进制与二进制存在天生的亲戚关系，转化起来不用经过十进制，可以飞快转：　 \large 0x33=(0011~0011)_2 \large 0x55=(0101~0101)_2

规律:每个十六进制数位，都可以转为4位二进制，然后拼在一起即可。

本题核心：用二进制+位运算+暴算

16、删去第7行与第14行的unsigned,程序行为不变。(√)

解答：short与unsigned~ short只差一个符号位，short是15位，而unsigned~ short是16位。从上面的推导可以知道，我们最多使用了8位，是不是有符号不是很重要，可以去掉。

答案：正确

17、将第7行与第13行的short均改为char,程序行为不变。(×)

解答：数字0的ASCII码是48,如果如果x=2,按char去接入，则用48+2=50去计算结果，原来是2,现在是50,结果肯定不一样啊，答案错误。

18、程序总是输出一个整数 0。（×）

解答：很明显，上面已经算出了答案，并不是0,答案错误。

19、当输入为2~2时，输出为 10。（×）

如果x=2,y=2,则按代码一行一行的代入计算即可


\large \left\{\begin{matrix}
x=(0010)_2 & \\ 
y=(0010)_2 & 
\end{matrix}\right.

x=2 , y=2
x=  	 0000 0010
x<<2     0000 1000

x=  	 0000 0010
|x<<2    0000 1000
--------------------------
         0000 1010
& 0x33   0011 0011
--------------------------
x=       0000 0010
x<<1     0000 0100
--------------------------------------
         0000 0110
& 0x55   0101 0101
-------------------------------------
x        0000 0100

y=       0000 0100
y<<1 =   0000 1000
| x      0000 0100 
z=   ----------------------
         0000 1100 =>12

y= 0010

结果：\large 00001100，结果应该是12。答案错误。

20、当输入为2~2时，输出为59。（×）

解答：不解释。

单选题

21、当输入为13~8时，输出为(B)

A.0 ~~~~ B.209 ~~~~ C.197 ~~~~ D.226

最终x=81=(0101 0001)_2,y=64=(01000000)_2

答案应该：2^7+2^6+2^4+2^0=128+64+16+1=209

x= 13 y=8

x  	0000 1101
|x<<2	0011 0100
---------------------------
        0011 1101
&0x33   0011 0011
-------------------------
        0011 0001
|x<<1   0110 0010
----------------------------
        0111 0011
&0x55   0101 0101
----------------------------
        0101 0001


y          0000 1000
|y<<2      0010 0000
-------------------------
           0010 1000
&0x33      0011 0011
-------------------------
           0010 0000
|y<<1      0100 0000
--------------------------
           0110  0000        
& 0x55     0101  0101
--------------------------
           0100   0000
y<<1       1000  0000
|x         0101 0001
---------------------
           1101 0001

128+64+16+1=209

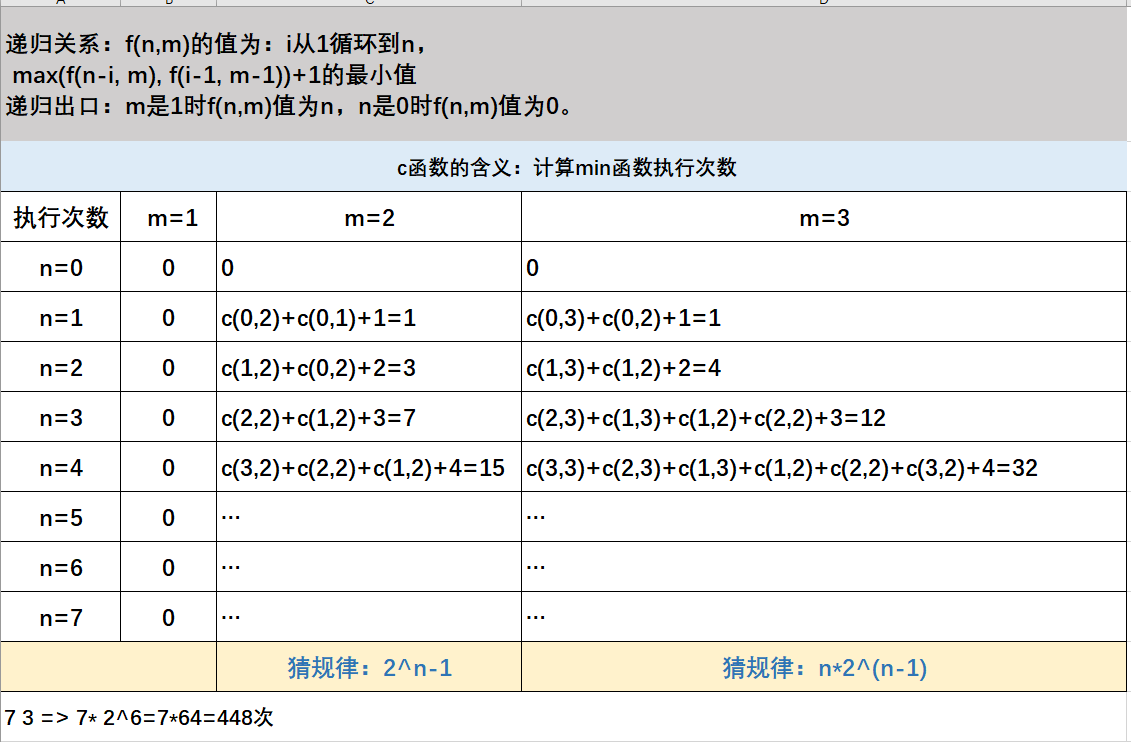
22、阅读程序回答问题

20221103140355

  • 先看选择项目，再看题面
  • 看明白哪个简单，就先做哪个，挑数字小的开整
  • 打表，对，打表，因为无论是递推，递归，动态规划，都可以用打表来理解

(1)、知识点：

numeric_limits:C++中取极值的方法，比如numeric_limits(int)::max就是取INT_MAX

(2)、递推与递归

上面一个递归，后面一个是递推，看来是一个问题的两种解法。

(3)、解题路径:大力出奇迹，打表过样例

20221103145428

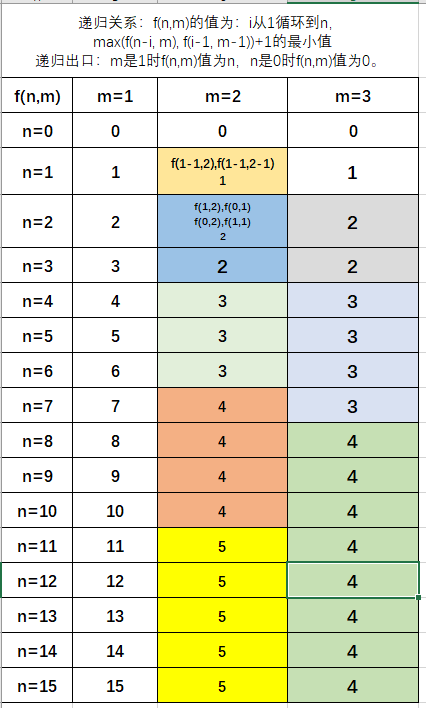
  • 现在让我们求的是7,3,也就是求7*2^{7-1}=7*2^6=7*64=448 判断题说结果是449，应该是说法错误。

  • 因为当m=100时，n的变化规律为1个1，2个2，4个3，8个4，16个5，32个6，最后剩下37个7，因此结果是7。

阅读程序第3题

20220922092212

黄海的二分总结

(4)、深入思考：扔鸡蛋问题

漫画：有趣的扔鸡蛋问题

漫画：什么是动态规划？（整合版）

20220922084218

\large dp(k,n)=\mathop{min}\limits_{0<=i<=n}\{max\{dp(k-1,i-1),dp(k,n-i)\}+1\}

结论：爆算+找规律

1 2~2 3~3~3 4~4~4~4 5~5~5~5~5 6~6~6~6~6~6

高空扔鸡蛋的代码

#include <bits/stdc++.h>

using namespace std;
const int N = 110;
int dp[N][N];

//在n层楼，剩余m个鸡蛋，返回最少的尝试次数
int f(int n, int m) {
    if (m == 1) return n;          //如果只有一个鸡蛋，那么需要枚举n层楼
    if (n == 0) return 0;          //如果没有楼，就不用再试了
    if (dp[n][m]) return dp[n][m]; //计算过就返回

    int ret = INT_MAX;
    for (int i = 1; i <= n; i++) //在当前场景下，尝试每一层楼进行扔鸡蛋，把所有可能计算出来，挑一个尝试次数最小的
        // f(n - i, m):鸡蛋没碎，楼层太矮，继续在i+1~n 这n-i层楼进行尝试,还有m个鸡蛋
        // f(i - 1, m - 1):鸡蛋碎了，楼层太高，继续在1~i-1层楼进行尝试
        // +1:代价是使用了一个次数
        ret = min(ret, max(f(n - i, m), f(i - 1, m - 1)) + 1); //
    return dp[n][m] = ret;
}

int g(int n, int m) {
    for (int i = 1; i <= n; i++) dp[i][1] = i;
    for (int j = 1; j <= m; j++) dp[0][j] = 0;

    for (int i = 1; i <= n; i++)
        for (int j = 2; j <= m; j++) {
            dp[i][j] = INT_MAX;
            for (int k = 1; k <= i; k++)
                dp[i][j] = min(dp[i][j], max(dp[i - k][j], dp[k - 1][j - 1]) + 1);
        }
    return dp[n][m];
}
int main() {
    int n, m;
    cin >> n >> m;

    cout << f(n, m) << endl
         << g(n, m) << endl;

    return 0;
}

阅读程序第3题

20220922092212

黄海的二分总结