20 KiB
CSP-J2019年初赛试题及详细解析
一、单项选择题
(共15题,每题2分,共计30分;每题有且仅有一个正确选项)
1. 中国的国家顶级域名是()
A. .cn B. .ch C. .chn D. .china
答案:A
考点:计算机基础-计算机网络-域名
解析:典型的国家顶级域名有 .cn (中国)、.us (美国)、.uk(英国)、.jp (日本)、.sg (新加坡)等。
典型的通用顶级域名有.edu(教育机构)、.gov (政府部门)、.net(网络组织)、.com (商业组织)、.org(非营机构)、.mil (军事部门)等。
2. 二进制数11 1011 1001 0111和01 0110 1110 1011进行逻辑与运算的结果 是()。
11 1011 1001 0111
&01 0110 1110 1011
------------------
01 0010 1000 0011
答案:D
考点:计算机基础-数制与编码-二进制-位运算
解析:逐位进行与运算。对于每一位,0与0得0, 1与0得0, 0与1得0, 1 与1得1。
3. 一个32位整型变量占用()个字节。
A. 32 B. 128 C. 4 D. 8
答案:C
考点:计算机基础-计算机体系结构-内存空间
解析:8位是1字节,因此32位是4字节。在C++语言中,int是最常用的带符 号32位整型变量,可表示数值:[-2^{31},2^{31}-1], unsigned int是最常用的无符号32位整型变量,可表示数值[0, 2^{32}-1]。
4. 若有如下程序段,其中s、a、b、c均已定义为整型变量,且a、c均已赋值(c 大于0)
s = a;
for (b = 1; b <= c; b++) s = s - 1;
则与上述程序段功能等价的赋值语句是()
A. s = a - c; B. s = a - b; C. s = s - c; D. s = b - c;
答案:A
考点:程序设计基础C++语法基础-循环语句
解析:s初始化为a,紧接着for循环c次,每次s减1,因此该程序段相当于
s=a-c。
5. 设有100个己排好序的数据元素,采用折半查找时,最大比较次数为()
A. 7~ B. 10 ~C. 6~ D. 8
答案:A
考点:程序设计基础-算法与数据结构-折半査找(二分査找)
解析:对100个有序元素进行折半查找,每次査找可将检索范围缩小一半。由 2^6-1<100<2^7-1可知,最大比较次数为7。
6. 链表不具有的特点是()
A.插入删除不需要移动元素 B.不必事先估计存储空间
C.所需空间与线性表长度成正比 D.可随机访问任一元素
答案:D 考点:程序设计基础-算法与数据结构-链表
解析:链表是通过记录每个元素的后继位置来实现数据存储,所需空间与元素个数成正比,优点是不必事先估计存储空间、插入或删除指定位置元素的时间复杂度为O(1);但缺点是由于其元素的内存地址不连续,无法进行O(1)的随机访问。
7. 把8个同样的球放在5个同样的袋子里,允许有的袋子空着不放,问共冇多少种不同的分法?()
提示:如果8个球都放在一个袋子里,无论是哪个袋子,都只算同一种分法
A. 22 ~ B. 24 ~ C. 18 ~ D. 20
答案:C
考点:数学-计数问题
解析:枚举法求解: 8个同样的球
- 分
1个袋子共1种方案- (8)
- 分
2个袋子共4种方案(1,7),(2,6),(3,5),(4,4)
- 分
3个袋子共5种方案(1,1,6),(1,2,5),(1,3,4),(2,2,4),(2,3,3)
- 分
4个袋子共5种方案(1,1,1,5),(1,1,2,4),(1,1,3,3),(1,2,2,3),(2,2,2,2)
- 分
5个袋子共3种方案(1,1,1,1,4),(1,1,1,2,3),(1,1,2,2,2)
合计1+4+5+5+3=18种。
总结:
- 枚举法需要查找递增的序列
- 枚举法有类似于进位的概念,需要特别注意
- 枚举法要注意去重
枚举法计数需要重点训练!
8、一棵二叉树如右图所示,若采用顺序存储结构,即用一维数组元素存储该二叉树中的结点(根结点的下标为1,若某结点的下标为i ,则其左孩子位于下标2i处、右孩子位于下标2i + 1处),则该数组的最大下标至少为( )。
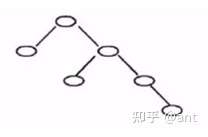
A. 6 ~B. 10 ~C. 15~ D. 12
答案:C
考点:程序设计基础-算法与数据结构-树结构
解析:根据题目给定的规则可知,下标最大的结点为树中深度最大且最靠右的结点,其下标为2^0+2^1+2^2+2^3=1+2+4+8=15。
9. 100以内最大的素数是( )。
A. 89~ B. 97~ C. 91~ D. 93
答案:B
考点:数学-素数与合数
解析:98 - 100均为合数,97为素数。
10.319和377的最大公约数是( )。
A. 27 ~B. 33~ C. 29~ D. 31
答案:C
考点:数学-公约数与公倍数
解析:使用辗转相除法可得 gcd(319, 377) =gcd(319, 58) =gcd(58, 29)=29。或将 两数分解质因数后,提取公共部分亦可求解。
11. 新学期开学了,小胖想减肥,健身教练给小胖制定了两个训练方案。
方案一:每次连续跑3公里可以消耗300千卡(耗时半小时):
方案二:每次连续跑5公里可以消耗600千卡(耗时1小时)。
小胖每周周一到周四能抽出半小时跑步,周五到周日能抽出一小时跑步。另外,教练建议小胖每周最多跑21公里,否则会损伤膝盖。请问如果小胖想严格执行教练的训练方案,并且不想损伤膝盖,每周最多通过跑步消耗多少千卡?( )
A. 3000 ~B. 2500 ~C. 2400 ~D. 2520
答案:C
考点:程序设计基础-算法与数据结构-枚举算法
解析:设方案1执行x天,方案2执行y天,则有3x+5y<=21 x<=4, y<=3。要求300x+600y的最大值,枚举可得最优方案为x=2、y=3,此时300x+600y为 2400。或使用线性规划亦可求解。
贪心:在y尽量大的情况下去尝试,应该价值最大。
y=3时,x=2,此时300x+600y=300*2+600*3=2400
12. 一副纸牌除掉大小王有52张牌,四种花色,每种花色13张。假设从这52张 牌中随机抽取13张纸牌,则至少( )张牌的花色一致。
A. 4 ~B. 2 ~C. 3~ D. 5
答案:A
考点:数学-抽屉原理
解析:最坏情况,13张牌对应四种花色的牌数为3、3、3、4。
尽量均匀分布,才能使得各个花色数量尽量一致,使最多的不太突出
13. 一些数字可以颠倒过来看,例如0、1、8颠倒过来还是本身,6颠倒过来是
9,9颠倒过来看还是6,其他数字颠倒过来都不构成数字。类似的,一些多位数也可以颠倒过来看,比如106颠倒过来是901。假设某个城市的车牌只由5位数字组成,每一位都可以取0到9。请问这个城市最多有多少个车牌倒过来恰好还是原来的车牌?( )
A. 60 ~B. 125~ C. 75 ~D. 100
答案:C
考点:数学-乘法原理
解析:前2位有0、1、8、6、9共5种选择,第3位只能放0、1、8,后2位由前2位决定,因此总方案数为5*5*3=75。
好题!不这样训练乘法原理,就不知道这东西怎么考查!
14. 假设一棵二叉树的后序遍历序列为DGJHEBIFCA,中序遍历序列为DBGEHJACIF, 则其前序遍历序列为( )。
A. ABCDEFGIHJ
B. ABDEGHJCFI
C. ABDEGJHCFI
D. ABDEGHJFIC
答案:B
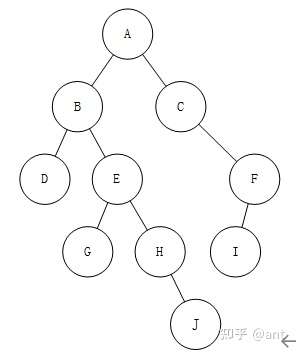
解析:后序遍历的规则是左右根、中序遍历的规则是左根右,因此可知, A是树根、DBGEHJ是A左子树的中序遍历(对应后续遍历DGJHEB)、CIF是A右子树的中序遍历(对应后续遍历IFC),递归画出对应的二叉树,再根据前序遍历规则根左右即可求出答案。
根据后序遍历和中序遍历求前序遍历,是高频考点,需要训练: 练习I 练习II 练习III 练习IV 已知前序后序为什么无法求出唯一中序
15. 以下哪个奖项是计算机科学领域的最高奖?()
A.图灵奖 B.鲁班奖 C.诺贝尔奖 D.普利策奖
答案:A
考点:计算机基础-常识-重要人物
解析:图灵奖由美国计算机协会于1966年设立,其名称取自计算机科学之父图灵,专门奖励对计算机事业作出重要贡献的个人,被誉为“计算机界的诺贝尔奖” 。
二、阅读程序

考点:程序设计基础-算法与数据结构-字符串
概述:程序用于将字符串下标(如果从1开始编号,但C++语言中实际是从0开始编号)是n约数的对应小写字母转换为大写字母。
判断题
1) 输入的字符串只能由小写字母或大写字母组成。( )
答案:错
解析:输入的字符串也可以包含数字等其他字符。
2) 若将第8行的i = 1改为i = 0,程序运行时会发生错误。( )
答案:对
解析:若i可以为0,则第9行的if语句条件n % i == 0将发生运行时错误RE。
3) 若将第8行的i <= n改为i * i <= n,程序运行结果不会改变。( )
答案:错
解析:当第8行的循环条件为i<=n时,字符串的末尾字符会被程序加工,但若改为i*i<=n,字符串的末尾字符将不会被程序加工(除非字符串长度为1)。 注意是开根号,这不对,比如14位,质因子分解为2 \times 7,7这个质因子就是大于\sqrt{14},如果只枚举到\sqrt{14},就会有一个大因子没有遍历到。
4) 若输入的字符串全部由大写字母组成,那么输出的字符串就跟输入的字符串一样。( )
答案:对
解析:大写字母的ASCII编码值小于小写字母的。若输入的字符串全部由大写字母组成,则程序不会对其进行加工。
•选择题
5) 若输入的字符串长度为18,那么输入的字符串跟输出的字符串相比,至多有( )个字符不同。
A. 18 ~ B. 6 ~ C. 10 ~ D. 1
答案:B
解析:18的正约数共有6个,因此程序至多修改输入字符串中的6个字符,即输出字符串与输入字符串至多有6个字符不同。
6) 若输入的字符串长度为( ),那么输入的字符串跟输出的字符串相比,至多有36个字符不同。
A. 36 ~ B. 100000~ C. 1~ D. 128
答案:B
解析:根据程序的作用可知,要使输出字符串和输入字符串之间至多有36个字符不同,36应当是字符串长度n的约数个数。本题选项中,仅有100000满足要求,将其分解质因数得100000=2^5*5^5,根据约数个数定理,得其的正约数共有(5+1)*(5+1)=36个。
程序二

假设输入的n和m都是正整数,x和y都是在[1, n]的范围内的整数,完成下面的判断题和单选题:
写在前面,方法总结
- 由于没有专门训练过阅读程序这样逆向思维的试题,导致阅读起来理解有困难,需要总结技巧。
- 不要上来就试图读懂整个代码的逻辑流程,应该从边界入手,从实例入手,从分支入手,去验证问题,不一定非得完整的把代码搞清楚它的原本含义。一般常见的例子举
3行,比如:
1 2
2 3
3 4
- 数字一般从
1开始,能简单就尽量简单。 - 不要指望一组模拟数据就能过掉所有问题,可能需要两组或以上
考点:程序设计基础-算法与数据结构-模拟算法 此题见17.xls的表格模拟测试数据解法。
程序三

考点:程序设计基础-算法与数据结构-树结构
概述:程序可以视作根据二叉树的中序遍历(根左右),构造一棵满足要求的树,并输出各结点深度与b值的加权和——要求二叉树的根结点 最小(min),并递归要求左右子树的根结点最小(除非相应子树为空)。
判断题
1)如果a数组有重复的数字,则程序运行时会发生错误。( )
答案:错
解析:若a数组有重复数字,则程序在根据a数组递归构造符合要求的二叉树时,对于相同结点值,会优先考虑位于左侧的。
2)如果b数组全为0,则输出为0。( )
答案:对
解析:程序最终输出的是各结点深度与b值的 加权和,因此若b数组全为0,则加权和显然为0。
选择题
3) 当n=100时,最坏情况下,与第12行的比较运算执行的次数最接近的是( )。
A. 5000 B. 600 C. 6 D. 100
答案:A
解析:最坏情况下,程序所构造的二叉树的每个结点至多仅有一个子结点,此时, 程序将递归100层,其中第i层进行100-i+1次第12行的比较运算,总执行次数为 100+99+98+…+ 1≈5000。
4) 当n=100时,最好情况下,与第12行的比较运算执行的次数最接近的是( )。
A. 100 B. 6 C. 5000 D. 600
答案:D
解析:最佳情况下,程序构造二叉树时,对于每个结点会尽可能均分其左右子树。 定义根结点深度为1,则含n=100个结点的树的深度最小为logn≈7,此时每选定一层结点,程序都需要执行约n次的第12行的比较运算,因此总执行次数约为 nlogn≈600。
5) 当n=10时,若b数组满足,对任意0 ≤ i < n。都有b[i] = i + 1,那么输出最大为( )。
A. 386 B. 383 C. 384 D. 385
答案:D
解析;
构造数据[1,2,3,4,5,6,7,8,9,10]
会发现,这是一棵从左上到右下的链,深度为10
此时,要使输出的ans值尽可能大,程序所构造的二叉树的深度应尽可能的大。定义根结点深度为1,则含10个结点的二叉树的最大深度为10,因此ans 的最大值为 1*1+2*2+3*3+…+10*10=385。
6) (4分)当n=100时,若b数组满足,对任意0 ≤ i < n,都有b[i]=1,那么输出最小为( )。
A. 582 B. 580 C. 579 D. 581
答案:B
解析:此时,要使输出的ans值尽可能小,程序应参照完全二叉树构造此树,其中深度为1的结点共1个,深度为2的结点共2个,深度为3的结点共4个…… 深度为6的结点共32个,剩余37个结点的深度为7,因此ans的最小值为(1*1+2*2+3*4+…+6*32)+7*37=580。
三、完善程序(单选题,每题3分,共计30分)
程序一


考点:程序设计基础-算法与数据结构-分治算法
概述:程序釆用分治算法,递归模拟矩阵的变换过程。递归函数recursive(x, y, n, t)表示计算左上角(x, y),大小2^n*2^n由单个数字t变幻而来的矩阵。
- ①处应填( )
A. n \% 2 B. 0 C. t D. 1
答案:C
解析:此处为递归边界,当需要计算的是单位矩阵时,相应元素应赋值为t,即无需再经任何变换。
2)②处应填( )
A. x – step , y – step B. x,y - step
C. x – step , y D. x, y
答案:D
解析:左上角(x,y),且大小2^n*2^n的矩阵,可以分成4个2^n-1*2^n-1的矩阵分别计算。此处需要计算的是4个矩阵中位于左上方的矩阵,该矩阵的左上角坐标为(x, y)。
3)③处应填( )
A. x - step, y - step B. x + step, y + step
C. x - step, y D. x, y – step
答案:B
解析:左上角(x,y),且大小2^n*2^n的矩阵,可以分成4个2^n-1*2^n-1的矩阵分别计算。此处需要计算的是4个矩阵中位于右下方的矩阵,该矩阵的左上角坐标为 (x+2^n-1, y+2^n-1)。
4) ④处应填()
A. n - 1, n % 2 B. n, 0
C. n, n % 2 D. n - 1, 0
答案:B
解析:此处是递归计算的入口,即题目最终所求的是大小2^n*2^n,由单个数字0变幻而来的矩阵,因此递归函数的后两个参数应设为n和0。
5)⑤处应填()
A. 1 << (n + 1) B. 1 << n
C. n + 1 D. 1 << (n - 1)
答案:B
解析:此处是计算最终所求的矩阵大小,即边长size为2^n,位运算写做 1<<n
程序二



考点:程序设计基础-算法与数据结构-排序算法
解析:基于计数排序,程序实际实现了近似于基数排序的算法——依次以低位到高位的每一位数为关键词,进行计数排序,前一次的排序结果是下一次的初始序列——本题对应着先根据第二关键词b进行计数排序,再根据第一关键词a进行计数排序。
- ①处应填()
A. ++cnt[i]
B. ++cnt[b[i]]
C. ++cnt[a[i] * maxs + b[i]]
D. ++cnt[a[i]]
答案:B
解析:此处是根据第二关键词b进行计数排序,并做各关键词的数量统计工作, 因此将b[i]对应的元素数量自增1。
2) ②处应填()
A. ord[--cnt[a[i]]] = i
B. ord[--cnt[b[i]]] = a[i]
C. ord[--cnt[a[i]]] = b[i]
D. ord[--cnt[b[i]]] = i
答案:D
解析:此处是根据第二关键词b进行计数排序,并记录排序结果。此时的ent[key] 用于表示关键词为key的元素在结果数组中的位置,因此这里的程序应将关键词为b[i]的元素i放在ord数组里。
3) ③处应填()
A. ++cnt[b[i]]
B. ++cnt[a[i] * maxs + b[i]]
C. ++cnt[a[i]]
D. ++cnt [i]
答案:C
解析:此处是根据第一关键词a进行计数排序,并做各关键词的数量统计工作, 因此将a[i]对应的元素数量自增1。
4) ④处应填()
A. res[--cnt[a[ord[i]]]] = ord[i]
B. res[--cnt[b[ord[i]]]] = ord[i]
C. res[--cnt[b[i]]] = ord[i]
D. res[--cnt[a[i]]] = ord[i]
答案:A
解析:此处是根据第一关键词a进行计数排序,并记录排序结果。由于此前已经根据第二关键词b进行计数排序,此时第i个元素的原始下标实际为ord[i], 因此这里的程序应将关键词为a[ord[i]]的元素ord[i]放在res数组里。
5) ⑤处应填()
A. a[i], b[i]
B. a[res[i]], b[res[i]]
C. a[ord[res[i]]] , b[ord[res[i]]]
D. a[res[ord[i]]] , b[res[ord[i]]]
答案:B
解析:此处是按顺序输出排序结果。由于此前已经按照第二关键词、第一关键词完成了计数排序,此时第i个元素的原始下标实际为res[i]。