10 KiB
P9751 [CSP-J 2023] 旅游巴士
零:前导知识
https://www.bilibili.com/video/BV1ha4y1T7om/?vd_source=13b33731bb79a73783e9f2c0e11857ae
办法一:魔改Dijkstra
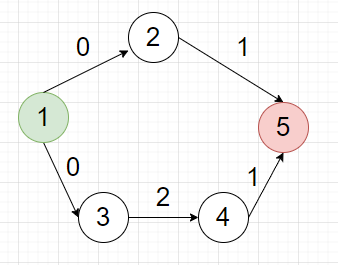
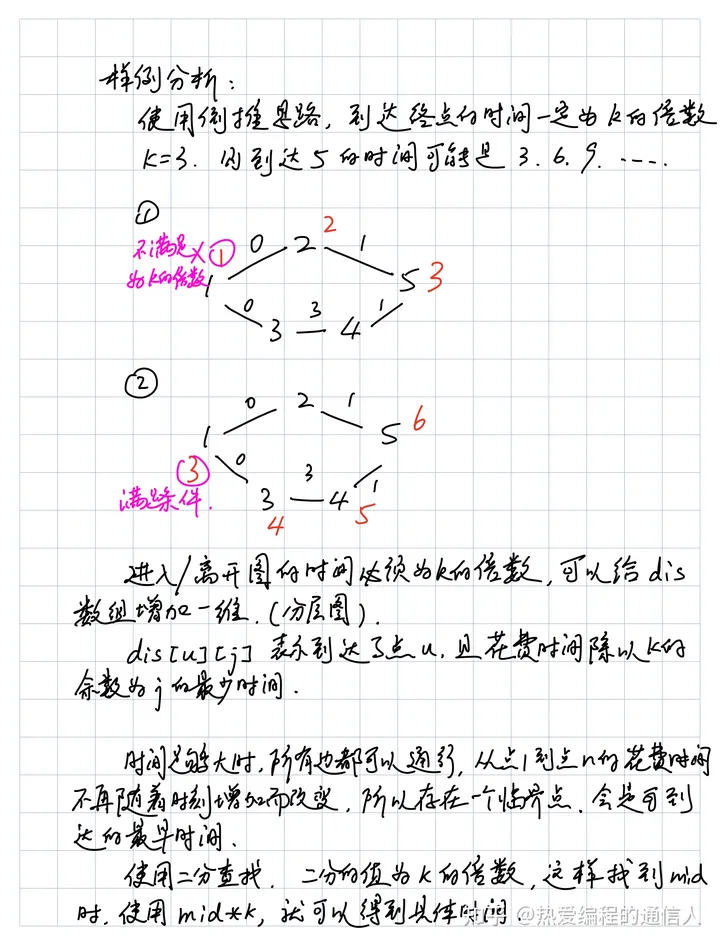
按测试用例进行分析题意:
1->2->5是走2步,不满足终点是3的倍数条件,而我们可以调整的余地也不大,只能是在起点时多等待3*m个时间后出发,在路径上其它点都不能进行等待。
那么,走到5号节点,原来是2,现在就是2+3*m的时间点,根据我们已有数学知识知道,这是不可能\%3=0的!
1->3->4->5是走3步,也就是\%3=0,那么,不就行了吗?不行!为什么呢?因为你看4号节点,如果从1节点在0时间出发,到达3号节点时是时间1,那么,4号节点要求时间2才能开放,你过不去啊!
怎么办?你只能是多等一个时间周期,也就是在节点1出发时不在0时刻出发,而是在0+3时间出发!这样,你在走4号节点时,就满足了3>2,就可以走了啊!
那问题来了,如果某个节点的时间要求不是数字2,而是x该怎么办呢?
其实我们需要保证到u号节点后,时间应该是t>=x的,如果现在t不是这样,那么需要一点点增大
while(t<x) t+=3;
也就是说,这才是符合条件的最小的限制条件t,不能再大了,因为再大就表示时间更长,人家要找的是最早的时间,当然越小越合适~
有了限制条件,那理想最短路径算法Dijkstra也不对了。
为什么呢?你想啊,理想的最短路,是在没有任何时间限制下的,我才不管你是不是允许通过,我看到路线就要通过,就能通过,现在不行了。
那该怎么办呢?还是以节点4为例,要求到达它,必须3需要保证到达时间为4, 1肯定是不行了,因为小于2嘛。
原来Dijkstra,进入队列的是一个二元结构体,一般喜欢用PII(因为小顶堆时可以不用写cmp方法,总结起来就是懒),而现在这么干肯定不行啊,因为现在需要一个三元的结构
① 节点编号
② 到达的最短路径 (到达的时间),需要满足大于下一步要走路径的开放时间
③ 目标点需要满足路径长度\%3=0,那么,前序节点需要满足\%3=1,再前序需要满足\%3=2,....
这是原始版本的
//迪杰斯特拉
void dijkstra(int start) {
memset(d, 0x3f, sizeof d); //初始化距离为无穷大
memset(st, 0, sizeof st); //初始化为未出队列过
priority_queue<PII, vector<PII>, greater<PII>> q; //小顶堆
q.push({0,start}); //出发点入队列
d[start] = 0; //出发点距离0
while (q.size()) {
auto t = q.top();
q.pop();
int u = t.second;
if (st[u]) continue;
st[u] = true;
for (int i = h[u]; ~i; i = ne[i]) {
int j = e[i];
if (d[j] > d[u] + w[i]) {
d[j] = d[u] + w[i];
q.push({d[j], j});
}
}
}
}
那就整一个三元组吧:
struct Node {
int u, r, d; // u节点编号,r状态,d最短到达时间
// 重载 < ,优先队列,默认使用大顶堆,我们需要小顶堆,所以,需要重载小于号,描述两个Node对比,
// 距离大的反而小,由于是大顶堆,所以距离小的在上
bool operator<(const Node t) const {
return d > t.d;
}
};
其它的就是一个Dijkstra模板了。对了,还有最重要的一个问题:
这个距离d,在原始版本中代表的是到达某个节点的最短距离,现在的题目中是
- 最短距离
- 到达某个节点+节点的
%3状态 比如现在倒数第二个节点最短距离是8,是通过1步过来的,记为d(u,1)=8
那么它对于终点就是没用的,不如最短距离是9,通过频数是2的,也就是d(u,2)=9
因为人家再走一步,就到终点了,你那个8使不上!
#include <bits/stdc++.h>
using namespace std;
const int N = 10010, M = N << 1, K = 110; // 节点个数上限,边数上限,发车间隔时长上限
const int INF = 0x3f3f3f3f; // Dijsktra专用正无穷
struct Node {
int u, r, d; // u节点编号,r状态,d最短到达时间
// 重载 < ,优先队列,默认使用大顶堆,我们需要小顶堆,所以,需要重载小于号,描述两个Node对比,
// 距离大的反而小,由于是大顶堆,所以距离小的在上
bool operator<(const Node t) const {
return d > t.d;
}
};
// 链式前向星
int e[M], h[N], idx, w[M], ne[M];
void add(int a, int b, int c = 0) {
e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx++;
}
/*
dis[u][i]表示到达第u处地点,并且到达时间mod k = i的情况下的最短距离
*/
int dis[N][K], st[N][K];
int main() {
memset(h, -1, sizeof h);
int n, m, k;
cin >> n >> m >> k;
for (int i = 0; i < m; i++) {
int a, b, c;
cin >> a >> b >> c;
add(a, b, c); // 从a到b建一条边,c权值为开放时间
}
// 初始状态,1号点在状态0时最短距离为0,其它点的最短距离为无穷大
memset(dis, 0x3f, sizeof dis); // dis是一个二维结果数组,一维是节点号,二维是此节点在不同状态下可以到达的最短路径
dis[1][0] = 0; // 所谓状态,是指到达时间(对于1号节点而言就是出发时间)%k的余数值
// 因为题目中说到,1号点和n号点都必须是%k=0的时间,所以,dis[1][0]=0
// 描述1号节点,在状态0下出发,距离出发点的距离是0
// 堆优化版Dijkstra求最短路,注意默认大顶堆,自定义比较规则
priority_queue<Node> q;
// 初始状态加入优先队列,{点,状态,最短到达时间}
q.push({1, 0, dis[1][0]}); // 节点号,%k的值,已经走过的距离
// 每个进队列的节点,都有3个属性:节点号,%k的值,已经走过的距离
while (q.size()) { // 从1号点开始宽搜
int u = q.top().u; // 节点编号u
int r = q.top().r; // 节点状态r
q.pop();
if (st[u][r]) continue; // 该状态已经加入到集合中,也就是已经被搜索过
// 先被搜索过在队列宽搜中意味着已经取得了最短路径
st[u][r] = 1;
for (int i = h[u]; ~i; i = ne[i]) { // 枚举邻接点v和连接到v节点道路的开放时间
int v = e[i]; // v节点,也就是下一个节点
int t = w[i]; // v节点的开放时间
int d = dis[u][r]; // 到达(u,p)这个状态时的最短距离d
int j = (r + 1) % k; // v节点的状态应该是u节点的状态+1后再模k
// 如果到达时间小于开放时间,则将到达时间向后延长若干个k的整数倍(向上取整)
while (d < t) d += k;
// 如果可以松弛到v点的时间
if (dis[v][j] > d + 1) { // 下一个节点v的j状态,可以通过(u,i)进行转移,那么可以用t+1更尝试更新掉dis[v][j]
dis[v][j] = d + 1;
q.push({v, j, dis[v][j]}); // 再用(v,j)入队列去更新其它节点数据,标准的Dijkstra算法
}
}
}
if (dis[n][0] == INF) // 如果终点的模k=0状态存在数字,那么就是说可以获取到最短路径,否则就是无法到达为个状态
cout << -1 << endl;
else
cout << dis[n][0] << endl;
return 0;
}
办法二:二分+宽搜
疑问与解答:
Q:为什么要建反图?
答:举个栗子,比如从1出发有如下路径
#include <bits/stdc++.h>
using namespace std;
const int N = 10010, M = N << 1, K = 110;
// 链式前向星
int e[M], h[N], idx, w[M], ne[M];
void add(int a, int b, int c = 0) {
e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx++;
}
// 入队列的结构体
struct Node {
int id; // 节点号
int r; // %k的余数
};
int dis[N][K]; // 最短路径
int n, m, k; // n个节点,m条边,时间是k的整数倍,即 %k=0
bool bfs(int mid) {
memset(dis, -1, sizeof dis);
queue<Node> q;
dis[n][0] = mid * k;
q.push({n, 0});
while (q.size()) {
int u = q.front().id;
int r = q.front().r;
q.pop();
if (dis[u][r] == 0) continue; // 反着走,距离为0,就不需要继续走了,剪枝
for (int i = h[u]; ~i; i = ne[i]) {
int v = e[i]; // 前序节点
int p = (r - 1 + k) % k; // 前序节点合法状态
if (~dis[v][p]) continue; // 如果前序点的合法状态不等于-1,表示已经被宽搜走过了,根据宽搜的理论,就是已经取得了最短距离,不需要再走
if (dis[u][r] - 1 < w[i]) continue; // 现在的最短距离是dis[u][r],那么前序的距离应该是dis[u][r]-1,那么,如果dis[u][r]-1<w[i],就是表示到达时,开放时间未到,无法能行
// 修改合法前序点距离,为当前最小距离减1
dis[v][p] = dis[u][r] - 1;
// 入队列继续扩展
q.push({v, p});
}
}
if (dis[1][0] == -1)
return false;
else
return true;
}
int main() {
memset(h, -1, sizeof h);
cin >> n >> m >> k;
while (m--) {
int a, b, c;
cin >> a >> b >> c;
add(b, a, c);
}
int l = 0, r = (1e6 + 1e4) / k, ans = -1;
while (l < r) {
int mid = l + r >> 1;
if (bfs(mid)) {
ans = mid * k;
r = mid;
} else
l = mid + 1;
}
cout << ans << endl;
return 0;
}