8.4 KiB
AcWing 2769. 表达式
一、题目描述
小 C 热衷于学习数理逻辑。
有一天,他发现了一种特别的逻辑表达式。
在这种逻辑表达式中,所有操作数都是变量,且它们的取值只能为 0 或 1,运算从左往右进行。
如果表达式中有括号,则先计算括号内的子表达式的值。
特别的,这种表达式有且仅有以下几种运算:
与运算:a & b。当且仅当 a 和 b 的值都为 1 时,该表达式的值为 1。其余情况该表达式的值为 0。
或运算:a | b。当且仅当 a 和 b 的值都为 0
时,该表达式的值为 0。其余情况该表达式的值为 1。
取反运算:!a。当且仅当 a 的值为 0 时,该表达式的值为 1。其余情况该表达式的值为 0。
小 C 想知道,给定一个逻辑表达式和其中每一个操作数的初始取值后,再取反某一个操作数的值时,原表达式的值为多少。
为了化简对表达式的处理,我们有如下约定:表达式将采用后缀表达式的方式输入。
后缀表达式的定义如下:
如果 E 是一个操作数,则 E 的后缀表达式是它本身。
如果 E 是 E1 op E2 形式的表达式,其中 op 是任何二元操作符,且优先级不高于 E1、E2 中括号外的操作符,则 E 的后缀式为 E′1 E′2 op
,其中 E′1、E′2 分别为 E1、E2 的后缀式。
如果 E 是 (E1) 形式的表达式,则 E1 的后缀式就是 E 的后缀式。
同时为了方便,输入中:
a) 与运算符(&)、或运算符(|)、取反运算符(!)的左右均有一个空格,但表达式末尾没有空格。
b) 操作数由小写字母 x 与一个正整数拼接而成,正整数表示这个变量的下标。例如:x10,表示下标为 10 的变量 x10。
数据保证每个变量在表达式中出现恰好一次。
输入格式
第一行包含一个字符串 s,表示上文描述的表达式。
第二行包含一个正整数 n,表示表达式中变量的数量。表达式中变量的下标为 1,2,…,n。
第三行包含 n 个整数,第 i 个整数表示变量 xi 的初值。
第四行包含一个正整数 q,表示询问的个数。
接下来 q 行,每行一个正整数,表示需要取反的变量的下标。
注意,每一个询问的修改都是临时的,即之前询问中的修改不会对后续的询问造成影响。
数据保证输入的表达式合法。
变量的初值为 0 或 1。
输出格式
输出一共有 q 行,每行一个 0 或 1,表示该询问下表达式的值。
数据范围
对于 20% 的数据,表达式中有且仅有与运算(&)或者或运算(|)。
对于另外 30% 的数据,|s|≤1000,q≤1000,n≤1000。
对于另外 20% 的数据,变量的初值全为 0 或全为 1。
对于 100% 的数据,1≤|s|≤1×106,1≤q≤1×105,2≤n≤1×10^5。
其中,|s| 表示字符串 s 的长度。
输入样例1:
x1 x2 & x3 |
3
1 0 1
3
1
2
3
输出样例1:
1
1
0
二、解题思路
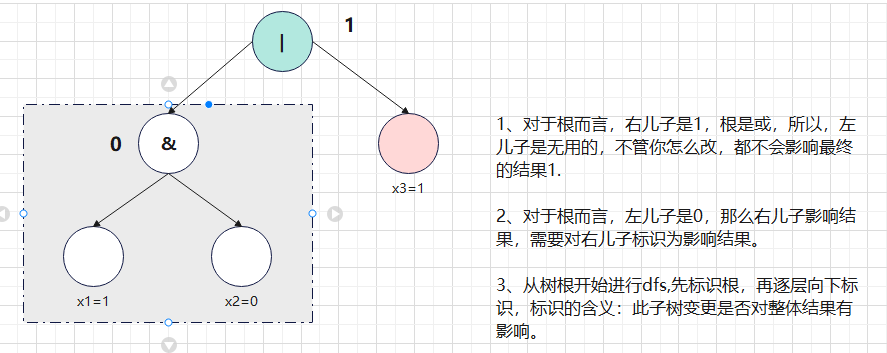
首先发现临时修改,自然地想到了先处理整个表达式的值,再考虑临时修改是否会有影响。
先建一颗表达式树。
我们发现:
对于一个有影响的子树
运算符号\&
- 如果左右子树都是
1,两个子树有一个值变更,都会影响根的值,打tag - 如果左右子树其中一个是
0,0子树更改会影响根的值,打tag
运算符号|
- 如果两个都是
0,两个子树有一个值变更,都会根的值,打tag - 如果其中一个是
1,1的子树变更会对根造成影响,打tag
运算符号取反!
直接取反即可
三、实现代码
#include <bits/stdc++.h>
using namespace std;
const int N = 1000010, M = N << 1;
int n; // 变量个数
int w[N]; // 变量参数的值
char c[N]; // 操作符栈
int stk[N], tt; // 数字栈
bool st[N]; // 是不是对
// 邻接表
int e[M], h[N], idx, ne[M];
void add(int a, int b) {
e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
// 第一次dfs求原后缀表达式,记录每个节点的计算值
int dfs1(int u) {
if (u <= n) return w[u]; // 叶子节点,返回参数值
if (c[u] == '!') // 如果当前节点是运算符!的话,那么,它一定只有一个子节点,节点号:h[u],值:e[h[u]],取反返回即可
w[u] = !dfs1(e[h[u]]);
else {
// 与和或
int a = e[h[u]], b = e[ne[h[u]]]; // 取当前节点左儿子和右儿子
if (c[u] == '&')
w[u] = dfs1(a) & dfs1(b); // 左儿子与右儿子的与运算结果
else
w[u] = dfs1(a) | dfs1(b); // 左儿子与右儿子的或运算结果
}
return w[u]; // 返回计算结果值
}
// 从根开始,标记哪些节点影响表达式的值
void dfs2(int u) {
st[u] = true; // 因为
if (u <= n) return; // 递归到叶子返回
if (c[u] == '!') { // 取反操作符
dfs2(e[h[u]]); // 前进,继续标记节点
return;
}
int a = e[h[u]], b = e[ne[h[u]]]; // 左右儿子节点号
if (c[u] == '&') { // &运算
if (w[a]) dfs2(b); // 左儿子=1,对右子树递归标记
if (w[b]) dfs2(a); // 右儿子=1,对左子树递归标记
} else { // |运算
if (!w[a]) dfs2(b); // 左儿子=0,递归右子树,右子树中的某些节点变化会对根造成影响
if (!w[b]) dfs2(a); // 右儿子=0,递归左儿子,左子树中的某些节点变化会对根造成影响
}
}
int main() {
string s;
getline(cin, s);
cin >> n; // 参数个数
for (int i = 1; i <= n; i++) scanf("%d", &w[i]); // 每个参数对应的数值
memset(h, -1, sizeof h); // 邻接表初始化
// 为了创建一个表达式树,就需要给每个节点创建一个编号。现在已知数字节点,也就是叶子节点数量是n
// 所以,运算符的编号就是从++m开始的。
int m = n;
// 后缀表达式->栈->建图
// 利用栈进行辅助建图,图才能进行dfs计算
for (int i = 0; i < s.size(); i++) {
if (s[i] == ' ') continue;
if (s[i] == 'x') {
int k = 0;
i++; // 跳过x
while (i < s.size() && isdigit(s[i])) k = k * 10 + s[i++] - '0';
stk[++tt] = k;
} else if (s[i] == '!') {
c[++m] = s[i]; //++m这个节点,表达式树中是s[i]这个操作符,
/* 表达式树:
(1)每个叶子节点的数值
(2)非叶子节点需要记录是什么操作符
记录办法
(1)以树中的节点编号为索引,[1~n]为叶子,[n+1~]为操作符
(2)再开一个数组char c[],记录操作符节点是哪个操作符
*/
add(m, stk[tt--]); // 从栈中弹出一个数字,因为是!嘛,树是由上到下的连单向边
stk[++tt] = m; // m节点入栈,方便后续构建
} else {
c[++m] = s[i];
add(m, stk[tt--]); // 与!不同,需要由m引向两个节点各一条边
add(m, stk[tt--]);
stk[++tt] = m;
}
}
// 计算原式结果
int res = dfs1(m); // 这个m才是根,因为是后缀表达式
// 标记哪些节点影响最终结果
dfs2(m);
for (int i = 1; i <= m; i++) {
cout << "i=" << i << ",st[" << i << "]=" << st[i] << ",c[" << i << "]=" << c[i] << endl;
}
int Q;
cin >> Q; // 询问个数
while (Q--) {
int x;
cin >> x; // 修改哪个变量
if (st[x]) // 如果x被打过标记,那么它的变化将会影响根节点的值,对根节点取反即可
printf("%d\n", !res);
else // 不会影响根节点的值
printf("%d\n", res);
}
return 0;
}