|
|
## [$AcWing$ $414$. 数字游戏](https://www.acwing.com/problem/content/416/)
|
|
|
|
|
|
### 一、题目描述
|
|
|
丁丁最近沉迷于一个数字游戏之中。
|
|
|
|
|
|
这个游戏看似简单,但丁丁在研究了许多天之后却发觉原来在简单的规则下想要赢得这个游戏并不那么容易。
|
|
|
|
|
|
游戏是这样的,在你面前有一圈整数(一共 $n$ 个),你要按顺序将其分为 $m$ 个部分,各部分内的数字相加,相加所得的 $m$ 个结果对 $10$ 取模后再相乘,最终得到一个数 $k$。
|
|
|
|
|
|
游戏的要求是使你所得的 $k$ 最大或者最小。
|
|
|
|
|
|
例如,对于下面这圈数字($n=4,m=2$):
|
|
|
|
|
|

|
|
|
|
|
|
|
|
|
当要求 **最小值** 时,$((2−1)\ mod \ 10)×((4+3) \ mod\ 10)=1×7=7$
|
|
|
当要求 **最大值** 时,$((2+4+3)\ mod\ 10)×(−1\ mod\ 10)=9×9=81$
|
|
|
|
|
|
特别值得注意的是,无论是负数还是正数,对 $10$ 取模的结果均为非负值。
|
|
|
|
|
|
丁丁请你编写程序帮他赢得这个游戏。
|
|
|
|
|
|
**输入格式**
|
|
|
输入文件第一行有两个整数,$n$ 和 $m$。
|
|
|
|
|
|
以下 $n$ 行每行一个整数,其绝对值不大于 $10000$,按顺序给出圈中的数字,首尾相接。
|
|
|
|
|
|
**输出格式**
|
|
|
输出文件有两行,各包含一个非负整数。
|
|
|
|
|
|
第一行是你程序得到的最小值,第二行是最大值。
|
|
|
|
|
|
**数据范围**
|
|
|
$1≤n≤50,1≤m≤9$
|
|
|
|
|
|
**输入样例**:
|
|
|
```cpp {.line-numbers}
|
|
|
4 2
|
|
|
4
|
|
|
3
|
|
|
-1
|
|
|
2
|
|
|
```
|
|
|
|
|
|
**输出样例**:
|
|
|
```cpp {.line-numbers}
|
|
|
7
|
|
|
81
|
|
|
```
|
|
|
|
|
|
### 二、题目解析
|
|
|
($DP$,区间$DP$) $O(n^3m)$
|
|
|
|
|
|
首先 **将环从起点处断开,然后复制一遍接在后面**,这样原问题就转化成了线段型的模型。
|
|
|
|
|
|
> **注:破环成链**
|
|
|
```cpp {.line-numbers}
|
|
|
n = read(), m = read();
|
|
|
for (int i = 1; i <= n; i ++ ){
|
|
|
w[i] = read();
|
|
|
w[i + n] = w[i]; //破环成链
|
|
|
}
|
|
|
```
|
|
|
然后 **从集合角度来分析状态表示和状态计算**:
|
|
|
|
|
|
**状态表示**
|
|
|
|
|
|
$f[l][r][k]$:所有将区间$[l,r]$划分成$k$部分方案的乘积 **最大值**
|
|
|
$g[l][r][k]$:所有将区间$[l,r]$划分成$k$部分方案的乘积 **最小值**
|
|
|
|
|
|
**状态计算**
|
|
|
|
|
|
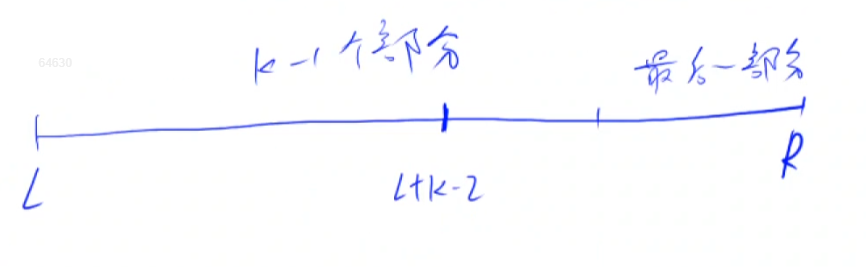
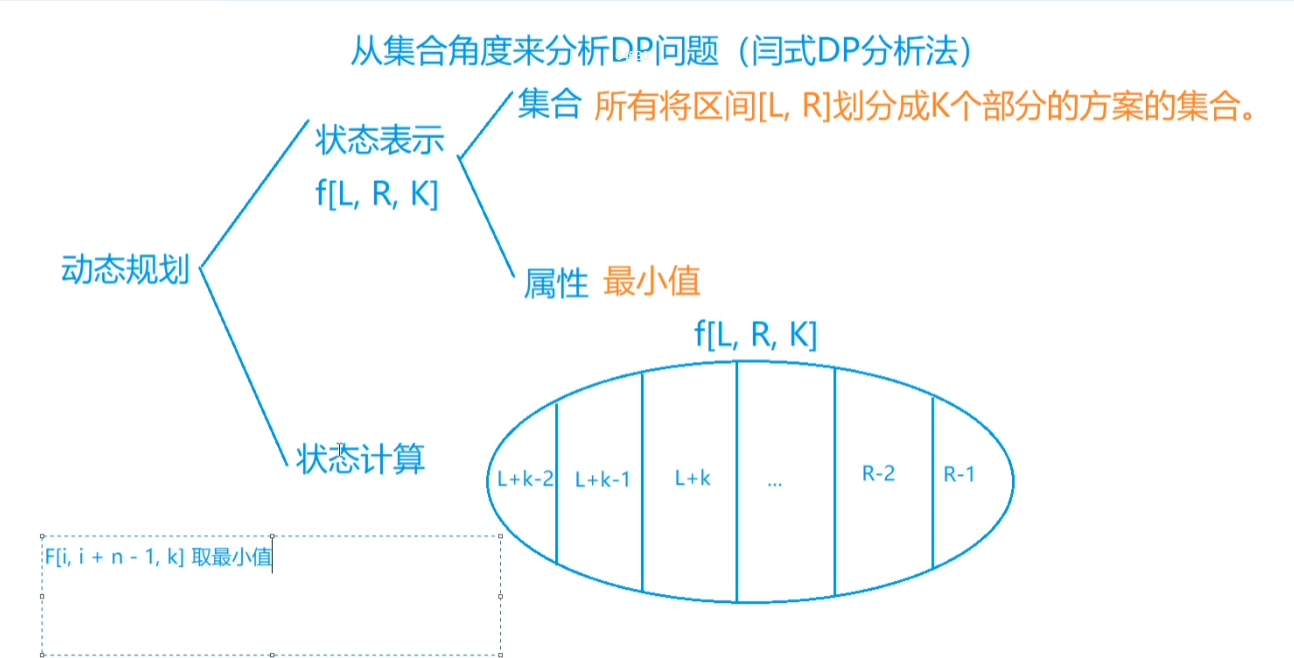
考虑$f[l][r][k]$如何计算获得,关键是寻找 **集合划分的依据**,划分依据一般选取 **最后一步的操作**,所以这里我们可以 **按最后一部分的位置来将$f[l][r][k]$所表示的所有方案划分成若干类**:
|
|
|
|
|
|
|
|
|
> <font color='red' size=4><b>注:上面的是数字的点,而不是区间,不要混淆!可能会造成理解错误~</b></font>
|
|
|
|
|
|
|
|
|
> <font color='red' size=4><b>注:第$k$个部分,肯定是从$k-1$个部分转移而来,现在考虑的是划分完$k-1$部分后,最后一个点的所有可能性$[l+k-2,r-1]$</b></font>
|
|
|
|
|
|
不妨设原$k-1$部分的终点是$j$,所以
|
|
|
$$\large l+k-2<=j<=r-1$$
|
|
|
> <font color='red' size=4><b>注:$j$是可以遍历的</b></font>
|
|
|
|
|
|
|
|
|
|
|
|
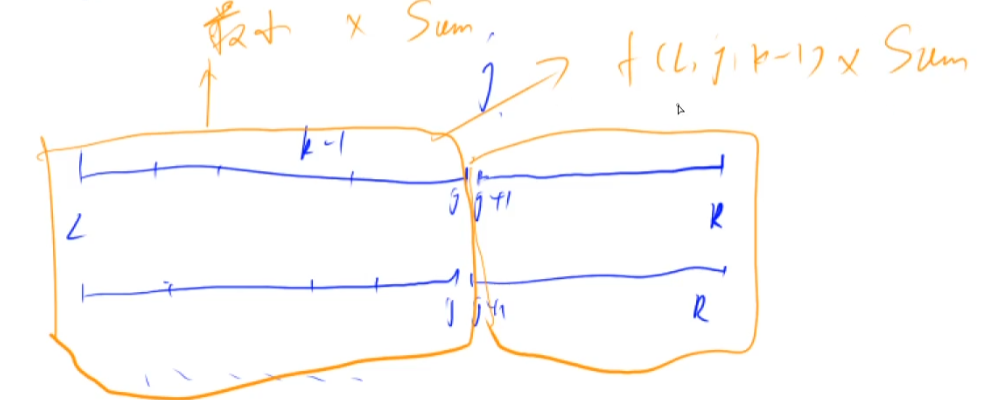
思考增加了第$k$个部分,最大值、最小值怎么求呢?
|
|
|
|
|
|
前$k-1$个部分的终点是$j$,第$k$个部分的起点是从$[j+1,r]$的任意一个值。
|
|
|
就是
|
|
|
$$\large f[l][r][k]= f[l][j][k-1] * (sum(r)-sum(j+1)) \\
|
|
|
\large g[l][r][k]= g[l][j][k-1] * (sum(r)-sum(j+1))$$
|
|
|
|
|
|
>**解释**:
|
|
|
因为对于每个方案而言,它的得分就是前面的数乘上后面的数。
|
|
|
由于每个数都是非负的,如果我希望我最终的结果是最大值或最小值,而且,现在后面黄色方框中的数字大小是固定的,所以,前面最大就是整体最大,前面最小就是整体最小。
|
|
|
|
|
|
最终枚举所有长度是$n$的区间,取最大值/最小值即可。
|
|
|
$\large f[i][i+n][m] \\
|
|
|
\large g[i][i+n][m]$
|
|
|
|
|
|
**时间复杂度**
|
|
|
状态总共有 $O(n^2m)$ 个,计算每个状态需要 $O(n)$ 的计算量,因此总时间复杂度是 $O(n^3m)$。
|
|
|
|
|
|
### 三、实现代码
|
|
|
```cpp {.line-numbers}
|
|
|
#include <bits/stdc++.h>
|
|
|
using namespace std;
|
|
|
const int N = 110, M = 10, INF = 0x3f3f3f3f;
|
|
|
|
|
|
int n, m;
|
|
|
int w[N], s[N];
|
|
|
int f[N][N][M], g[N][N][M];
|
|
|
|
|
|
int get_mod(int x) {
|
|
|
return (x % 10 + 10) % 10;
|
|
|
}
|
|
|
|
|
|
int main() {
|
|
|
cin >> n >> m;
|
|
|
for (int i = 1; i <= n; i++) {
|
|
|
cin >> w[i];
|
|
|
w[i + n] = w[i]; // 破环成链
|
|
|
}
|
|
|
for (int i = 1; i <= n * 2; i++) s[i] = s[i - 1] + w[i]; // 预处理前缀和,下标从1开始
|
|
|
|
|
|
memset(f, 0x3f, sizeof f); // 预求最小,先设最大
|
|
|
memset(g, -0x3f, sizeof g); // 预求最大,先设最小
|
|
|
|
|
|
for (int len = 1; len <= n; len++) // 区间DP,先枚举长度
|
|
|
for (int l = 1; l + len - 1 <= n * 2; l++) { // 枚举起点
|
|
|
int r = l + len - 1; // 计算终点
|
|
|
// DP 初始化
|
|
|
// 边界条件是全部划分为k=1,也就是一块时的结果是多少,根据题意,一整块当然就是区间内容相加后对10取模
|
|
|
f[l][r][1] = g[l][r][1] = get_mod(s[r] - s[l - 1]);
|
|
|
// 状态转移
|
|
|
for (int k = 2; k <= m; k++) // 枚举每个可以划分成的部分
|
|
|
for (int j = l + k - 2; j <= r - 1; j++) { // 枚举K-1部分时的最后一个终点位置
|
|
|
f[l][r][k] = min(f[l][r][k], f[l][j][k - 1] * get_mod(s[r] - s[j]));
|
|
|
g[l][r][k] = max(g[l][r][k], g[l][j][k - 1] * get_mod(s[r] - s[j]));
|
|
|
}
|
|
|
}
|
|
|
|
|
|
// 枚举每个区间长度为n的区间,获取符合长度要求的区间内,划分成m块的最大、最小值
|
|
|
int mx = -INF, mi = INF;
|
|
|
for (int i = 1; i <= n; i++) {
|
|
|
mx = max(mx, g[i][i + n - 1][m]);
|
|
|
mi = min(mi, f[i][i + n - 1][m]);
|
|
|
}
|
|
|
cout << mi << endl;
|
|
|
cout << mx << endl;
|
|
|
return 0;
|
|
|
}
|
|
|
``` |