|
|
## [$AcWing$ $2770$. 方格取数](https://www.acwing.com/problem/content/2772/)
|
|
|
|
|
|
### 一、题目描述
|
|
|
设有 $n×m$ 的方格图,每个方格中都有一个整数。
|
|
|
|
|
|
现有一只小熊,想从图的左上角走到右下角,每一步只能向上、向下或向右走一格,并且不能重复经过已经走过的方格,也不能走出边界。
|
|
|
|
|
|
小熊会取走所有经过的方格中的整数,求它能取到的整数之和的最大值。
|
|
|
|
|
|
**输入格式**
|
|
|
第 $1$ 行两个正整数 $n,m$。
|
|
|
|
|
|
接下来 $n$ 行每行 $m$ 个整数,依次代表每个方格中的整数。
|
|
|
|
|
|
**输出格式**
|
|
|
一个整数,表示小熊能取到的整数之和的最大值。
|
|
|
|
|
|
**数据范围**
|
|
|
对于 $20\%$ 的数据,$n,m≤5$。
|
|
|
对于 $40\%$ 的数据,$n,m≤50$。
|
|
|
对于 $70\%$ 的数据,$n,m≤300$。
|
|
|
对于 $100\%$ 的数据,$1≤n,m≤1000$。
|
|
|
方格中整数的绝对值不超过 $10^4$。
|
|
|
|
|
|
**输入样例1**:
|
|
|
```cpp {.line-numbers}
|
|
|
3 4
|
|
|
1 -1 3 2
|
|
|
2 -1 4 -1
|
|
|
-2 2 -3 -1
|
|
|
```
|
|
|
|
|
|
**输出样例1**:
|
|
|
```cpp {.line-numbers}
|
|
|
9
|
|
|
```
|
|
|
|
|
|
**样例1解释**
|
|
|
|
|
|
|
|
|
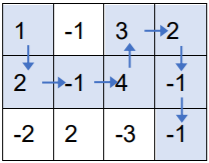
按上述走法,取到的数之和为 $1+2+(−1)+4+3+2+(−1)+(−1)=9$,可以证明为最大值。
|
|
|
|
|
|

|
|
|
|
|
|
注意,上述走法是错误的,因为第 $2$ 行第 $2$ 列的方格走过了两次,而根据题意,不能重复经过已经走过的方格。
|
|
|
|
|
|
|
|
|
|
|
|
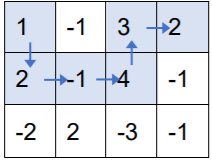
另外,上述走法也是错误的,因为没有走到右下角的终点。
|
|
|
|
|
|
**输入样例2:**
|
|
|
```cpp {.line-numbers}
|
|
|
2 5
|
|
|
-1 -1 -3 -2 -7
|
|
|
-2 -1 -4 -1 -2
|
|
|
```
|
|
|
|
|
|
**输出样例2:**
|
|
|
```cpp {.line-numbers}
|
|
|
-10
|
|
|
```
|
|
|
|
|
|
**样例2解释**
|
|
|
|
|
|
|
|
|
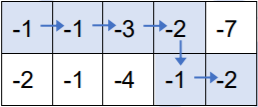
按上述走法,取到的数之和为 $(−1)+(−1)+(−3)+(−2)+(−1)+(−2)=−10$,可以证明为最大值。
|
|
|
|
|
|
因此,请注意,取到的数之和的最大值也可能是负数。
|
|
|
|
|
|
### 二、题目解析
|
|
|
>$70pts$ 做法
|
|
|
$O(n2m)$ $DP$
|
|
|
|
|
|
先考虑按 **最普通的方格取数** 问题进行 $DP$。
|
|
|
|
|
|
转移方程:
|
|
|
$$\large f[i][j]=max(f[i][j−1],f[i−1][j],f[i+1][j])$$
|
|
|
|
|
|
**这样做是有后效性的**,即更新完 $f[i+1][j]$ 后可能会重复更新 $f[i][j]$。
|
|
|
|
|
|
那么就要想新的做法了。
|
|
|
|
|
|
由于不能往左走,所以 **在每列中走过的序列必然是连续的一段**。
|
|
|
|
|
|
一共有 $m$ 列,所以我们走出的路径必然是 $m$ 条竖着的段,并且每一段是相邻的。
|
|
|
|
|
|
又因为不能往回走,所以在每列中,只能一直向上走或一直向下走。
|
|
|
|
|
|
> <font color='red' size=4><b>注:</b></font>**结合样例理解一下**:
|
|
|
> 
|
|
|
|
|
|
|
|
|
这个性质启发我们 **枚举列** 进行 $DP$。
|
|
|
|
|
|
**$Q$:怎么保证先前的状态不会被改变呢?**
|
|
|
|
|
|
**答**:多开一个状态。
|
|
|
|
|
|
开出来两个状态数组,表示 **只向下+向右走** 和 **只向上+向右走** 可以到达$(i,j)$这个格子能拾取到的 **最大值**,这就将问题分成了两个问题:
|
|
|
|
|
|
- 能向右走或者向下走到达$(i,j)$这个格子可以取到的最大值;(相当于从左上角开始)
|
|
|
- 能向右走或者向上走到达$(i,j)$这个格子可以去到的最大值;(相当于从左下角开始)
|
|
|
|
|
|
两种问题取最大值就是答案。
|
|
|
|
|
|
#### 代码实现
|
|
|
```cpp {.line-numbers}
|
|
|
#include <bits/stdc++.h>
|
|
|
using namespace std;
|
|
|
typedef long long LL;
|
|
|
const int N = 1010;
|
|
|
|
|
|
int g[N][N]; // 原始地图
|
|
|
// 1e3 * 1e3 * 1e4 开longlong
|
|
|
LL f1[N][N]; // 向右+向下走
|
|
|
LL f2[N][N]; // 向右+向上走
|
|
|
int n, m;
|
|
|
/*
|
|
|
现象:
|
|
|
实测 max( max(a,b),max(c,d)) 795 ms
|
|
|
max({a,b,c,d}) 1200ms
|
|
|
|
|
|
结论:
|
|
|
放弃max({a,b,c,d}),这个太慢了
|
|
|
*/
|
|
|
int main() {
|
|
|
// 加快读入
|
|
|
ios::sync_with_stdio(false), cin.tie(0);
|
|
|
cin >> n >> m;
|
|
|
|
|
|
for (int i = 1; i <= n; i++)
|
|
|
for (int j = 1; j <= m; j++)
|
|
|
cin >> g[i][j];
|
|
|
|
|
|
memset(f1, -0x3f, sizeof f1); // 有负数,初始化为-INF
|
|
|
memset(f2, -0x3f, sizeof f2); // 有负数,初始化为-INF
|
|
|
|
|
|
f1[1][1] = f2[1][1] = g[1][1]; // 左上角的数必须拿起来
|
|
|
|
|
|
for (int j = 1; j <= m; j++) { // 第一层循环列数
|
|
|
// 用上一列两种问题的状态更新这一列的状态达到最优 //行数之间也要更新最优的状态
|
|
|
for (int i = 1; i <= n; i++) // 因为是向下走,所以从第一行开始循环
|
|
|
f1[i][j] = max(max(f1[i][j - 1], f2[i][j - 1]) + g[i][j], max(f1[i][j], f1[i - 1][j] + g[i][j]));
|
|
|
|
|
|
for (int i = n; i >= 1; i--) // 因为是向上走,所以从第N行开始循环
|
|
|
f2[i][j] = max(max(f1[i][j - 1], f2[i][j - 1]) + g[i][j], max(f2[i][j], f2[i + 1][j] + g[i][j]));
|
|
|
}
|
|
|
|
|
|
cout << f1[n][m] << endl;
|
|
|
// cout << max(f1[n][m], f2[n][m]);
|
|
|
// 两种问题取最优(其实不用去max因为{N, M}的格子只能从上面走下来,所以直接去f1[n][m]即可)
|
|
|
return 0;
|
|
|
}
|
|
|
``` |