7.4 KiB

Raw Blame History Unescape Escape

This file contains ambiguous Unicode characters that may be confused with others in your current locale. If your use case is intentional and legitimate, you can safely ignore this warning. Use the Escape button to highlight these characters.

`AcWing` `463`. 求和

一、题目描述

一条狭长的纸带被均匀划分出了 n 个格子，格子编号从 1 到 n。

每个格子上都染了一种颜色 color_i（用 [1，m] 当中的一个整数表示），并且写了一个数字 number_i。

定义一种特殊的三元组：(x,y,z)，其中 x，y，z 都代表纸带上格子的编号，这里的三元组要求满足以下两个条件：

x,y,z 都是整数, x<y<z,y−x=z−y
color_x=color_z

满足上述条件的三元组的分数规定为 (x+z)∗(number_x+number_z)。

整个纸带的分数规定为所有满足条件的三元组的分数的和。

这个分数可能会很大，你只要输出整个纸带的分数除以 10,007 所得的余数即可。

输入格式 第一行是用一个空格隔开的两个正整数 n 和 m，n 代表纸带上格子的个数，m 代表纸带上颜色的种类数。

第二行有 n 个用空格隔开的正整数，第 i 个数字 number_i 代表纸带上编号为 i 的格子上面写的数字。

第三行有 n 个用空格隔开的正整数，第 i 个数字 color_i 代表纸带上编号为 i 的格子染的颜色。

输出格式 共一行，一个整数，表示所求的纸带分数除以 10,007所得的余数。

数据范围 1≤n,m≤10^5,1≤number_i≤10^5, 1≤color_i≤m

输入样例：

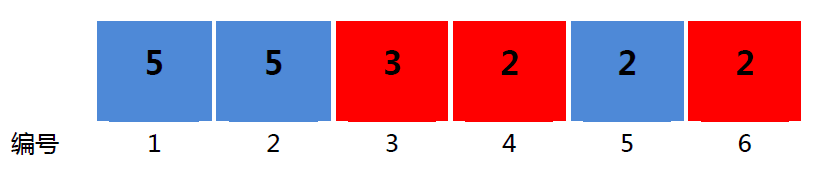
6 2
5 5 3 2 2 2
2 2 1 1 2 1

输出样例：

二、暴力枚举

40分 O(n^2)

三元组：(x, y, z)要求满足以下两个条件：

x,y,z 都是整数, x<y<z,y−x=z−y
color_x=color_z 那么：x+z=2y。由此可以枚举x和y的值，如果颜色相同，累加分值即可。

时间复杂度 O(n^2)

#include <bits/stdc++.h>
using namespace std;

const int N = 100010, mod = 10007;

int a[N], color[N];

int main() {
    int n, m; // 纸带上格子的个数,纸带上颜色的种类数
    cin >> n >> m;

    for (int i = 1; i <= n; i++) cin >> a[i];     // 纸带上编号为 i 的格子上面写的数字
    for (int i = 1; i <= n; i++) cin >> color[i]; // 纸带上编号为 i 的格子染的颜色

    int res = 0;
    for (int x = 1; x <= n; x++) {
        for (int y = x + 1; 2 * y - x <= n; y++) { // 因为y>=x+1,并且z<=n
            int z = 2 * y - x;
            if (color[x] == color[z]) // 如果color[x]=color[z]
                res = (res + (2 * y) % mod * (a[x] + a[z]) % mod) % mod;
        }
    }
    printf("%d\n", res);
    return 0;
}

三、优化

读题，我们发现完全可以暴力O(n^{3})

那这必然过不了

观察题目，对式一进行移项，发现x+z=2y

<<<<<<< HEAD https://www.acwing.com/solution/content/20931/

不妨设一个分组里有n个格子，x_i 表示格子的编号，w_i表示格子上的数字。那么这个分组的得分：

$ans=(x_1+x_2)(w_1+w_2)+(x_1+x_3)(w_1+w_3)+…+(x_1+x_n)(w_1+w_n) \ \ \ \ \ +(x_2+x_3)(w_2+w_3)+(x_2+x_4)(w_2+w_4)+… \ \ \ \ \ +(x_2+x_n)(w_2+w_n) +(x_3+x_4)(w_3+w_4)+…+(x_3+x_n)(w_3+w_n) +… + … +(x_{n−1}+x_n)(w_{n−1}+w_n)$

于是我们便可以枚举x,z或y

当然这个复杂度也是过不了的

f6696ab196bedd79de6ffd3091b6a46ab435f7be

做到这个地步，我们似乎基本没有用到颜色

<<<<<<< HEAD $ans=x_1[(w_1+w_2)+(w_1+w_3)+(w_1+w_4)…+(w_1+w_n)] +x_2[(w_1+w_2)+(w_2+w_3)+(w_2+w_4)+…+(w_2+w_n)] +x_3[(w_1+w_3)+(w_2+w_3)+(w_3+w_4)+…+(w_3+w_n)] +… + … +x_n[(w_1+w_n)+(w_2+w_n)+(w_3+w_n)+…+(wn−1+w_n)] =x_1[(n−1)w_1+w_2+w_3+w_4+…+w_n] +x_2[(n−1)w_2+w_1+w_3+w_4+…+w_n] +x_3[(n−1)w_3+w_1+w_4+w_5+…+w_n] +… + … +x_n[(n−1)w_n+w_1+w_2+w_3+…+w_{n−1}]$

于是我们便可以向颜色上靠，可以利用分组的思想，将同一颜色分成一组，又根据x+z=2y

可以 把相同颜色的分为奇偶两组

`Q`:怎么得出最后答案呢?

我们可以对分数的计算：(x+z)*(number_{x}+number_{z}) 进行一定的处理(数学变形)

设c[i]为第i个格子的颜色
cnt[c[i]][i\%2]为颜色为c[i]的两个奇偶分组中数字个数

设x_i为下标，w_i为值

$ans=(x_1+x_2)(w_1+w_2)+(x_1+x_3)(w_1+w_3)+…+(x_1+x_n)(w_1+w_n) \ \ \ \ \ \ \ \ \ \ +(x_2+x_3)(w_2+w_3)+(x_2+x_4)(w_2+w_4)+…+(x_2+x_n)(w_2+w_n)\ \ \ \ \ \ \ \ \ \ +(x_3+x_4)(w_3+w_4)+…+(x_3+x_n)(w_3+w_n)\ \ \ \ \ \ \ \ \ \ +… \ \ \ \ \ \ \ \ \ \ +(x_{n−1}+x_n)(w_{n−1}+w_n)$

将有关x_1的式子 提出来找规律

(x_1+x_2)*(w_1+w_2) +(x_1+x_3)*(w_1+w_3)...+ (x_1+x_n)*(w_1+w_n)

注：共n-1项

乘出来 $x_1 * w_1 + x_1 * w_2 +x_2 * w_1+x_2 * w_2+ \ x_1 * w_1 + x_1 * w_3 +x_3 * w_1+x_3 * w_3+ \ ... \ +x_1 * w_1+ x_1w_n+x_nw_1+x_n*w_n$

将有关x_1的式子提出来

x_1*w_1+x_1*w_2+...+x_1*w_1+x_1*w_n

=(n-1)*x_1*w_1+x_1*(w_2+w_3+...+w_n)

将这个式子 +x_1*w_1-x_1*w_1 得

$\displaystyle \ \ \ \ \ \ (n-2)x_1w_1+x_1*(w_1+w_2+w_3+...+w_n) \ = x_1*((n-2)w_1+(w_1+w_2+w_3+...+w_n)) \ = x_1[(n-2)*w_1+\sum_{i=1}^nw_i]$

显然\displaystyle \sum_{i=1}^nw_i可以预处理出来。这个 n-2是什么呢？n应该是该分组中数字的总个数,这个也可以预处理出来~

`Code`

#include <bits/stdc++.h>
using namespace std;

const int N = 100010, mod = 10007;

int w[N]; // 第i个格子的数字
int c[N]; // 第i个格子的颜色
int s[N][2];
// s[i][0]:颜色为i、编号为偶数格子上数字的和
// s[i][1]:颜色为i、编号为奇数格子上数字的和

int cnt[N][2];
// cnt[i][0]:颜色为i、编号为偶数格子的个数
// cnt[i][1]:颜色为i、编号为奇数格子的个数

int main() {
    int n, m;
    cin >> n >> m;
    for (int i = 1; i <= n; i++) cin >> w[i]; // 第i个格子的数字
    // 预处理
    for (int i = 1; i <= n; i++) { // 遍历每个格子
        cin >> c[i];               // 格子颜色c[i]
        /*
        装入不同的组中,组划分是两个规则：
        ① 颜色必须相同
        ② 奇偶性必须相同
        所以，c[i]相同的放到同一个颜色组内，并且，在同一个颜色组内，奇偶数还必须相同。

        s[][]:随着i的不断向后遍历，s中记录了相同颜色，相同奇偶性的格子，数字的累加和
        cnt[][]:记录每个分组中的格子个数
        */
        s[c[i]][i % 2] = (s[c[i]][i % 2] + w[i]) % mod; // 累加分组内数字和
        cnt[c[i]][i % 2]++;                             // 维护分组内格子个数
    }

    int ans = 0;
    for (int i = 1; i <= n; i++) // 枚举每个格子
        /*
        Q:这个格子在哪个分组里呢？
        答：
        (1) c[i] : 按颜色划分
        (2) i % 2 : 按奇偶性划分

        Q:这个分组中格子的数量是多少呢？
        答： cnt[c[i]][i % 2]

        */
        ans = (ans + i * ((cnt[c[i]][i % 2] - 2) * w[i] % mod + s[c[i]][i % 2])) % mod;

    printf("%d\n", ans);
    return 0;
}

f6696ab196bedd79de6ffd3091b6a46ab435f7be

7.4 KiB Raw Blame History Unescape Escape

AcWing 463. 求和