|
|
## [$AcWing$ $432$. $Hanoi$双塔问题](https://www.acwing.com/problem/content/434/)
|
|
|
|
|
|
### 一.汉若单塔(也称经典汉若塔问题)
|
|
|
|
|
|
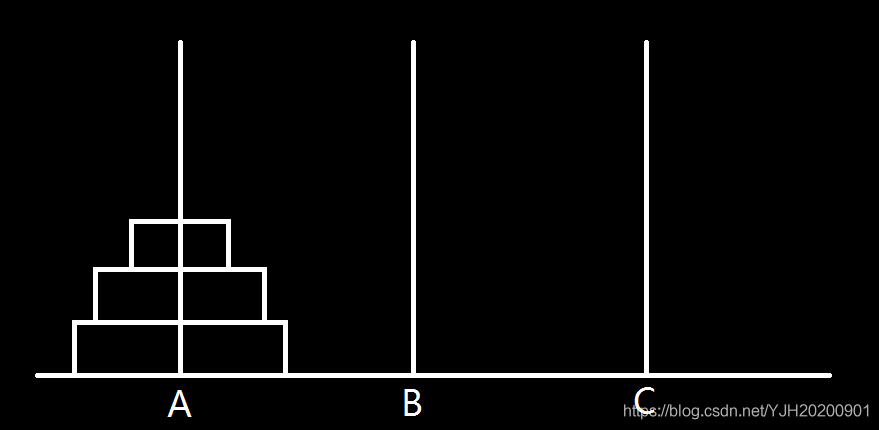
首先,我们先画个 $n=3$ 图:
|
|
|
|
|
|
|
|
|
|
|
|
要把 $A$ 柱上的 **圆盘** 移到 $C$ 柱上,要求无论在哪个柱子上的圆盘都是大的在下面,小的在上面。求从 $A$ 柱上的圆盘移到 $C$ 柱上要多少步?
|
|
|
|
|
|
#### 1. 实践
|
|
|
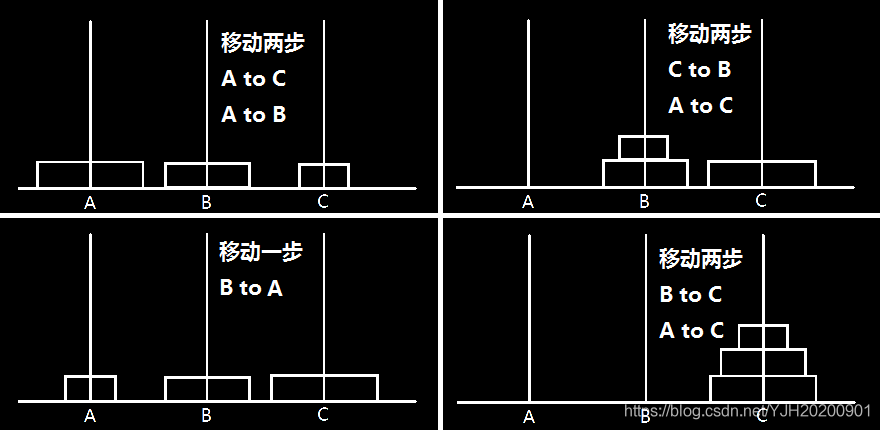
遇到这种问题,首先想到的是先模拟一次,如下图:
|
|
|
|
|
|
|
|
|
|
|
|
怎么样?看完过程,是不是清晰了许多?全过程是这样的:
|
|
|
|
|
|
<table>
|
|
|
<tr bgcolor=#EFF3F5>
|
|
|
<th>         步数        </th>
|
|
|
<th>        操作        </th>
|
|
|
</tr>
|
|
|
<tr>
|
|
|
<td align=center>1</td>
|
|
|
<td align=center>① A to C</td>
|
|
|
</tr>
|
|
|
<tr>
|
|
|
<td align=center>2</td>
|
|
|
<td align=center>② A to B</td>
|
|
|
</tr>
|
|
|
<tr>
|
|
|
<td align=center>3</td>
|
|
|
<td align=center>① C to B</td>
|
|
|
</tr>
|
|
|
<tr>
|
|
|
<td align=center>4</td>
|
|
|
<td align=center>③ A to C</td>
|
|
|
</tr>
|
|
|
<tr>
|
|
|
<td align=center>5</td>
|
|
|
<td align=center>① B to A</td>
|
|
|
</tr>
|
|
|
<tr>
|
|
|
<td align=center>6</td>
|
|
|
<td align=center>② B to C</td>
|
|
|
</tr>
|
|
|
<tr>
|
|
|
<td align=center>7</td>
|
|
|
<td align=center>① A to C</td>
|
|
|
</tr>
|
|
|
</table>
|
|
|
|
|
|
#### 2. 探索
|
|
|
>**解释**
|
|
|
① :最上面的第$1$个圆饼
|
|
|
② :中间的第$2$个圆饼
|
|
|
③ :最下面的第$3$个圆饼
|
|
|
|
|
|
总共$7$步。仔细观察我们可以发现,移动的盘子是对称的,如上表:$①②①③①②①$。
|
|
|
以$③$为点 ,左右对称。再看看右边$①②①$,也是对称的,这是 $n=2$ 时移动的步数。我们是不是可以推测出如果 $n=4$ 时,$①②①③①②①④①②①③①②①$是移动顺序呢?事实证明的确如此。移动顺序总是上一个序列加上新的盘子再加上一个序列。
|
|
|
> **注**
|
|
|
> 我终于懂了汉诺塔,真是太$TM$简单了~
|
|
|
|
|
|
由此可得递推公式:
|
|
|
$$\large f[i] =f[i−1] ∗2+1$$
|
|
|
|
|
|
[刘老师视频讲座](https://www.bilibili.com/video/BV1Rq4y1v7sC)
|
|
|
|
|
|
#### 3. 运用
|
|
|
如何运用到$c++$里面呢?
|
|
|
```cpp {.line-numbers}
|
|
|
int f[10010];
|
|
|
|
|
|
int n;
|
|
|
scanf ("%d", &n);
|
|
|
for (int i = 1 ; i <= n ; i++)
|
|
|
f[i] = f[i-1] * 2 + 1;
|
|
|
printf ("%d\n", f[n]);
|
|
|
```
|
|
|
这就是主程序。
|
|
|
|
|
|
#### 4. 思考
|
|
|
如何输出中间的步骤?可在评论区回答 `or` 讨论!
|
|
|
|
|
|
|
|
|
|
|
|
### 二.汉若双塔
|
|
|
|
|
|
#### 1. 认识
|
|
|
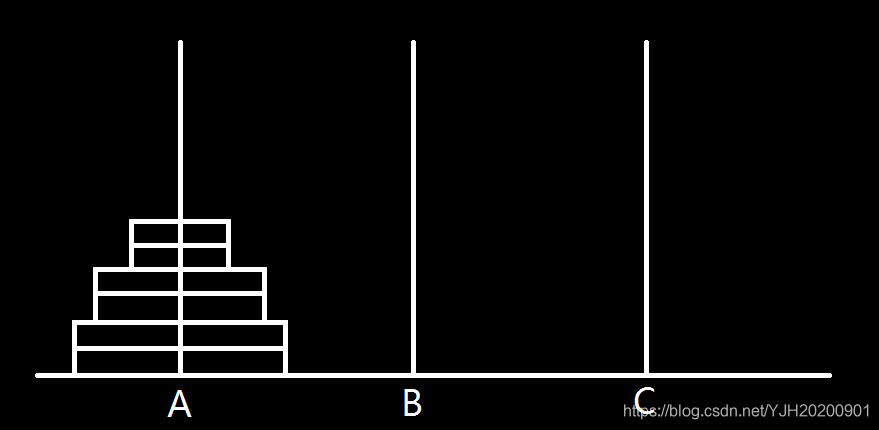
我们来看看汗若双塔长什么样子吧:
|
|
|
|
|
|
|
|
|
他就是每种型号多了$1$个盘子。移动起来的步骤也就乘$2$了。
|
|
|
|
|
|
|
|
|
#### 2. 实现
|
|
|
```cpp {.line-numbers}
|
|
|
int f[10010];
|
|
|
int n;
|
|
|
scanf ("%d", &n);
|
|
|
for (int i = 1 ; i <= n ; i++)
|
|
|
f[i] = f[i-1] * 2 + 1;
|
|
|
|
|
|
printf ("%d\n", f[n] * 2);
|
|
|
```
|
|
|
|
|
|
### 三.加强
|
|
|
当数据 $n<=200$ 时,我们应该怎么做? $answer$ :当然是 **无符号** $long$ $long$ 啦。
|
|
|
|
|
|
$NO!NO!NO!$ 我们应该开高精度,这才是正解!!!
|
|
|
|
|
|
康康 $code$ :
|
|
|
```cpp {.line-numbers}
|
|
|
#include <bits/stdc++.h>
|
|
|
using namespace std;
|
|
|
|
|
|
const int N = 100010;
|
|
|
|
|
|
// 加法高精度
|
|
|
int a[N], b[N];
|
|
|
int al, bl;
|
|
|
void add(int a[], int &al, int b[], int &bl) {
|
|
|
int t = 0;
|
|
|
al = max(al, bl);
|
|
|
for (int i = 1; i <= al; i++) {
|
|
|
t += a[i] + b[i];
|
|
|
a[i] = t % 10;
|
|
|
t /= 10;
|
|
|
}
|
|
|
if (t) a[++al] = 1;
|
|
|
}
|
|
|
|
|
|
int main() {
|
|
|
int n;
|
|
|
cin >> n;
|
|
|
b[++bl] = 1;
|
|
|
|
|
|
for (int i = 1; i <= n; i++) {
|
|
|
add(a, al, a, al);
|
|
|
add(a, al, b, bl);
|
|
|
}
|
|
|
|
|
|
// 最后再乘以2
|
|
|
add(a, al, a, al);
|
|
|
|
|
|
for (int i = al; i; i--) cout << a[i];
|
|
|
return 0;
|
|
|
}
|
|
|
```
|