|
|
## [$AcWing$ $424$. 循环](https://www.acwing.com/problem/content/426/)
|
|
|
|
|
|
### 一、题目描述
|
|
|
乐乐是一个聪明而又勤奋好学的孩子。
|
|
|
|
|
|
他总喜欢探求事物的规律。
|
|
|
|
|
|
一天,他突然对数的正整数次幂产生了兴趣。
|
|
|
|
|
|
众所周知,$2$ 的正整数次幂最后一位数总是不断的在重复 $2,4,8,6,2,4,8,6......$
|
|
|
我们说 $2$ 的正整数次幂最后一位的循环长度是 $4$(实际上 $4$ 的倍数都可以说是循环长度,但我们只考虑最小的循环长度)。
|
|
|
|
|
|
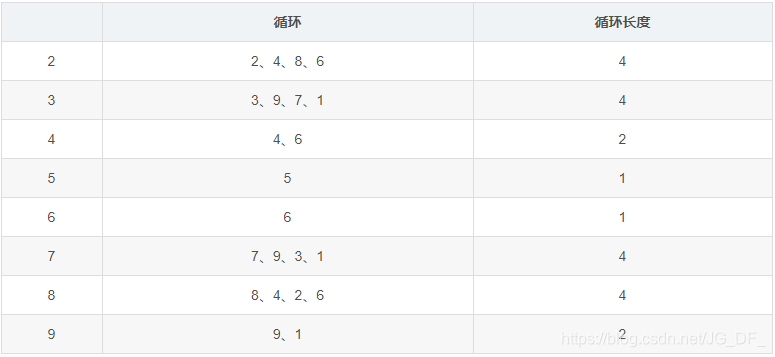
类似的,其余的数字的正整数次幂最后一位数也有类似的循环现象:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
这时乐乐的问题就出来了:是不是只有最后一位才有这样的循环呢?对于一个整数 $n$ 的正整数次幂来说,它的后 $k$ 位是否会发生循环?如果循环的话,循环长度是多少呢?
|
|
|
|
|
|
**注意**:
|
|
|
- 如果 $n$ 的某个正整数次幂的位数不足 $k$,那么不足的高位看做是 $0$。
|
|
|
- 如果循环长度是 $L$,那么说明对于任意的正整数 $a$,$n$ 的 $a$ 次幂和 $a+L$ 次幂的最后 $k$ 位都相同。
|
|
|
|
|
|
**输入格式**
|
|
|
输入文件只有一行,包含两个整数 $n$ 和 $k$,$n$ 和 $k$ 之间用一个空格隔开,表示要求 $n$ 的正整数次幂的最后 $k$ 位的循环长度。
|
|
|
|
|
|
**输出格式**
|
|
|
输出文件包括一行,这一行只包含一个整数,表示循环长度。
|
|
|
|
|
|
如果循环不存在,输出 `−1`。
|
|
|
|
|
|
**数据范围**
|
|
|
$1≤n≤10100,1≤k≤100$
|
|
|
|
|
|
**输入样例**:
|
|
|
```cpp {.line-numbers}
|
|
|
32 2
|
|
|
```
|
|
|
|
|
|
**输出样例**:
|
|
|
```cpp {.line-numbers}
|
|
|
4
|
|
|
```
|
|
|
|
|
|
**举栗子**:
|
|
|
|
|
|
$32^1=32 ,32^2=1024,32^3=32768,32^4=1048576$
|
|
|
$32^5=33554432,$
|
|
|
|
|
|
此时发现后$2$位开始循环,而循环节的长度是$4$
|
|
|
|
|
|
### 二、解题思路
|
|
|
一道模拟题,需要用到 **高精度乘法**。
|
|
|
|
|
|
首先,既然我们要求的是后 $k$ 位的循环节,那前面的循环节我们就不管了。
|
|
|
|
|
|
>**引理**:如果已知后 $k − 1$ 位的循环节,那么后 $k$ 位的循环节一定就是它的倍数。
|
|
|
|
|
|
开始模拟找规律,举栗子: $(8123, 4)$
|
|
|
>**解释**:
|
|
|
($8123$,$1$)指$8123$的后$1$位循环节;
|
|
|
($8123$,$2$)指$8123$的后$2$位循环节,
|
|
|
....
|
|
|
|
|
|
```cpp {.line-numbers}
|
|
|
8123 1
|
|
|
|
|
|
第 1 次:8123 * 8123 = 65983129
|
|
|
第 2 次:3129 * 8123 = 25416867
|
|
|
第 3 次:6867 * 8123 = 55780641
|
|
|
第 4 次:0641 * 8123 = 05206843
|
|
|
8123 ^ 4 = 4353773312630641
|
|
|
```
|
|
|
可以发现,在乘第 $4$ 次的时候,最后 $1$ 位出现了循环(数字$3$),循环节为 $4$ ,那么最后的答案一定就是 $4$ 的倍数。
|
|
|
|
|
|
>**解释**:如果最后一位想要重复出现,最小的循环数是$4$次。
|
|
|
|
|
|
如果把乘数换一下,不再是傻傻的用$8123$去一次次乘,而是换成 $0641$ ,即 $8123^4$ 的后 $4$ 位。这样乘 $1$ 次 $0641$ 就等于乘了 $4$ 次 $8123$ ,而且,乘 $0641$ 还能保证最后 $1$ 位永远是 $3$ ,因为 $8123^{4+1}$ 的最后一位都是 $3$ 。
|
|
|
|
|
|
这样,我们就可以不用再去管后 $1$ 位了,而去处理后 $2$ 位。
|
|
|
```cpp {.line-numbers}
|
|
|
8123 2
|
|
|
第 1 次:8123 * 0641 = 05206843
|
|
|
第 2 次:6843 * 0641 = 04386363
|
|
|
第 3 次:6363 * 0641 = 04078683
|
|
|
第 4 次:8683 * 0641 = 05565803
|
|
|
第 5 次:5803 * 0641 = 03719723
|
|
|
0641 ^ 5 = 108215668739201
|
|
|
```
|
|
|
最后 $2$ 位的循环节是 $5$,我们再把乘数换成 $9201$。
|
|
|
```cpp {.line-numbers}
|
|
|
8123 3
|
|
|
第 1 次:8123 * 9201 = 74739723
|
|
|
第 2 次:9723 * 9201 = 89461323
|
|
|
第 3 次:1323 * 9201 = 12172923
|
|
|
第 4 次:2923 * 9201 = 26894523
|
|
|
第 5 次:4523 * 9201 = 41616123
|
|
|
9201 ^ 5 = 65943979755726446001
|
|
|
```
|
|
|
|
|
|
```cpp {.line-numbers}
|
|
|
8123 4
|
|
|
第 1 次:8123 * 6001 = 48746123
|
|
|
第 2 次:6123 * 6001 = 36744123
|
|
|
第 3 次:4123 * 6001 = 24742123
|
|
|
第 4 次:2123 * 6001 = 12740123
|
|
|
第 5 次:0123 * 6001 = 00738123
|
|
|
```
|
|
|
|
|
|
我们继续处理完后 $3$ 位和后 $4$ 位,得出了每 $1$ 位的循环节,答案只要把它们累乘起来就可以了,即最后的答案为 $4×5×5×5=500$。
|
|
|
|
|
|
至此,我们求出了 $8123$后 $4$ 位的循环长度。
|
|
|
|
|
|
由于我们在处理的时候,已经确保了后面的数字都不变,那么我们只要考虑当前这 $1$ 位的循环节就行了,而 $1$ 位的循环节最多为 $10$ 。所以,我们处理每 $1$ 位的时候,就都只要处理 $10$ 次,如果还没出结果,那就直接输出 `-1` 并退出就行了。
|
|
|
|
|
|
因为我们每 $1$ 位最多处理 $10$ 次,每一次最多要耗费 $k^2$ 的时间,所以时间复杂度约 $O(k^3)$,妥妥地能过!
|
|
|
|
|
|
还要注意一点,最后的答案要用高精度,否则会因为超过 `long long` 的范围而答案错误。
|
|
|
|
|
|
```cpp {.line-numbers}
|
|
|
#include <bits/stdc++.h>
|
|
|
using namespace std;
|
|
|
|
|
|
const int N = 110;
|
|
|
|
|
|
int K; // 求最后K位的循环节长度是多少
|
|
|
int a[N]; // 原始数组
|
|
|
int b[N]; // 工作数组
|
|
|
int cnt[N] = {1}; // 次数,也就是答案
|
|
|
int st[10];
|
|
|
|
|
|
// 高精乘高精,限长K,结果保存到a数组中
|
|
|
void mul(int a[], int b[]) {
|
|
|
int c[N] = {0}; // 临时数组
|
|
|
for (int i = 0; i < K; i++) // 只保留尾部K个,对应高精度数组,就是0~K-1
|
|
|
for (int j = 0; j < K; j++)
|
|
|
if (i + j < K) c[i + j] += a[i] * b[j]; // 防止越界,需要加上i+j<K的限制
|
|
|
|
|
|
for (int i = 0, t = 0; i < K; i++) {
|
|
|
t += c[i]; // 进位与当前位置的和
|
|
|
a[i] = t % 10; // 余数保留下来
|
|
|
t /= 10; // 进位
|
|
|
}
|
|
|
}
|
|
|
|
|
|
// 输出高精度结果
|
|
|
void print(int a[]) {
|
|
|
int i = N - 1;
|
|
|
while (i > 0 && !a[i]) i--; // 去除前导零
|
|
|
while (i >= 0) cout << a[i--]; // 逐位输出
|
|
|
}
|
|
|
|
|
|
int main() {
|
|
|
string s; // 这里之所以用string类型,是为了照顾高精度同学
|
|
|
cin >> s >> K; // 求最后k个长度的循环节长度是多少
|
|
|
|
|
|
// 放入高精度计算数组,注意是倒着放的,下标从0开始
|
|
|
for (int i = s.size() - 1; i >= 0; i--) a[s.size() - 1 - i] = s[i] - '0';
|
|
|
|
|
|
for (int i = 0; i < K; i++) { // 执行K轮,从后往前,每轮固定一个尾部数字
|
|
|
memset(st, 0, sizeof st); // 某个数字是不是出现过,桶
|
|
|
memcpy(b, a, sizeof a); // b数组初始化
|
|
|
|
|
|
int j;
|
|
|
for (j = 1; j <= 10; j++) { // 最多执行10次
|
|
|
mul(b, a); // 开始乘a
|
|
|
|
|
|
// 对于高精度数组而言,头部即数字尾部
|
|
|
// 随着轮次的增加,我们希望检查的位置也发生了变化,位置下标为i
|
|
|
// 如果当前计算的结果中,当前的计算位置,出现与原数字一样的数字,那么就是找到了循环节,此时的j就是我们想要收集的
|
|
|
if (b[i] == a[i]) break;
|
|
|
|
|
|
// 如果某个数字重复出现,却一直没有和原始的一样,表示它自己的循环轨迹和原始的不一样,永远也不可以一样了,无解
|
|
|
if (st[b[i]]) {
|
|
|
puts("-1");
|
|
|
exit(0);
|
|
|
};
|
|
|
st[b[i]] = 1; // 记录出现过的数字
|
|
|
}
|
|
|
|
|
|
// ① 累计次数
|
|
|
int c[N] = {j}; // 需要乘的次数,这里有用高精度乘高精度模拟高精度乘低精度
|
|
|
// 注意:即使j=10,上面的高精度乘法依然是有效的,因为在高精度乘法的内部采用的是模10进位的办法
|
|
|
mul(cnt, c); // 将次数累乘起来
|
|
|
|
|
|
// ② 变更乘数
|
|
|
memcpy(b, a, sizeof a); // 重新装载原始数字
|
|
|
for (int k = 1; k < j; k++) mul(b, a); // 反复乘j-1次
|
|
|
memcpy(a, b, sizeof b); // a升级了
|
|
|
}
|
|
|
|
|
|
print(cnt); // 输出高精度数组内容
|
|
|
return 0;
|
|
|
}
|
|
|
``` |