You can not select more than 25 topics
Topics must start with a letter or number, can include dashes ('-') and can be up to 35 characters long.
This file contains ambiguous Unicode characters that may be confused with others in your current locale. If your use case is intentional and legitimate, you can safely ignore this warning. Use the Escape button to highlight these characters.
## [洛谷 $P1862$ 输油管道问题](https://www.luogu.com.cn/problem/P1862)
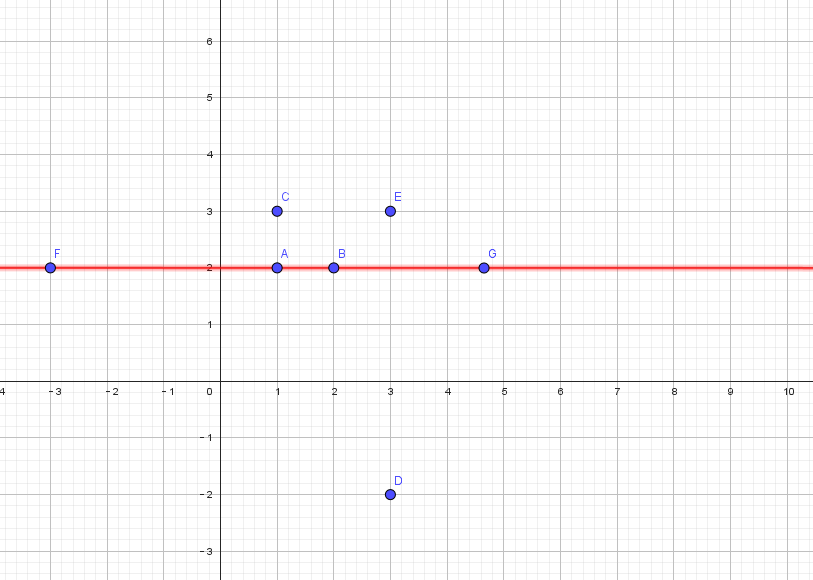
如果只有一口井,那么显然是越近越好。如果有两口井,那么显然是有以下三种情况:
- 两口井都在主管道北边,那么这个时候的两个连接管道的长度和肯定大于两口井的$Y$坐标之差。
- 两口井都在主管道南边,
- 两口井,一个在主管道南边,一个在主管道北边,那么两个连接管道的长度和就等于两口井的$Y$坐标之差。
显然情况三是所要的最短管道的设计情况。就是当主管道在两口井之间的任意位置时,连接管道长度之和都等于两口井的$Y$坐标之差,是最短的长度。
那么将这个结论推广,当有$n$口井的时候,
- $n$是偶数 只要这$n$口井分布在主管道的两边,一边$n/2$个,那么就是距离之和最小的。
- $n$是奇数,只要将这$n$个井中,$Y$坐标最中间的(也就是$Y$是中值的那个)井不算,其余的偶数个井分布在主管道的两侧,这个时候移动主管道,那么这$n$个连接管道长度之和就决定于那个没有算的井了,因为其余的井的距离之和是固定了的,这个时候只要主管道最接近那个点就好了。
也就是说,输油管道的位置就是最中间的那口井(或中间的区间)。我的方法是将各口井的$y$坐标排序($x$坐标不用管),再取 $n$ $div$ $2$+$1$ 的位置,即最中间的位置。
```cpp {.line-numbers}
#include <bits/stdc++.h>
const int N = 10005;
/*
文件名:
题目:洛谷 P1862 输油管道问题
题目网址:
输入:
5
1 2
2 2
1 3
3 -2
3 3
输出:
6
*/
int n, a[N]; // a[0..n-1]。第i口油井的纵坐标在a[i]
int main() {
// 输入数据
cin >> n;
for (int i = 0; i < n ; i ++) cin > > a[i] >> a[i]; // 横坐标说没有用的,可以直接抛弃掉
// 排序
sort(a, a + n);
// 两端对称取长短。中位数原理。
int sum = 0;
for (int i = 0, j = n - 1; i < = j; i++, j--) sum += a[j] - a[i];
cout < < sum << endl ;
return 0 ;
}
```