python

2.3 KiB

Raw Blame History Unescape Escape

This file contains ambiguous Unicode characters that may be confused with others in your current locale. If your use case is intentional and legitimate, you can safely ignore this warning. Use the Escape button to highlight these characters.

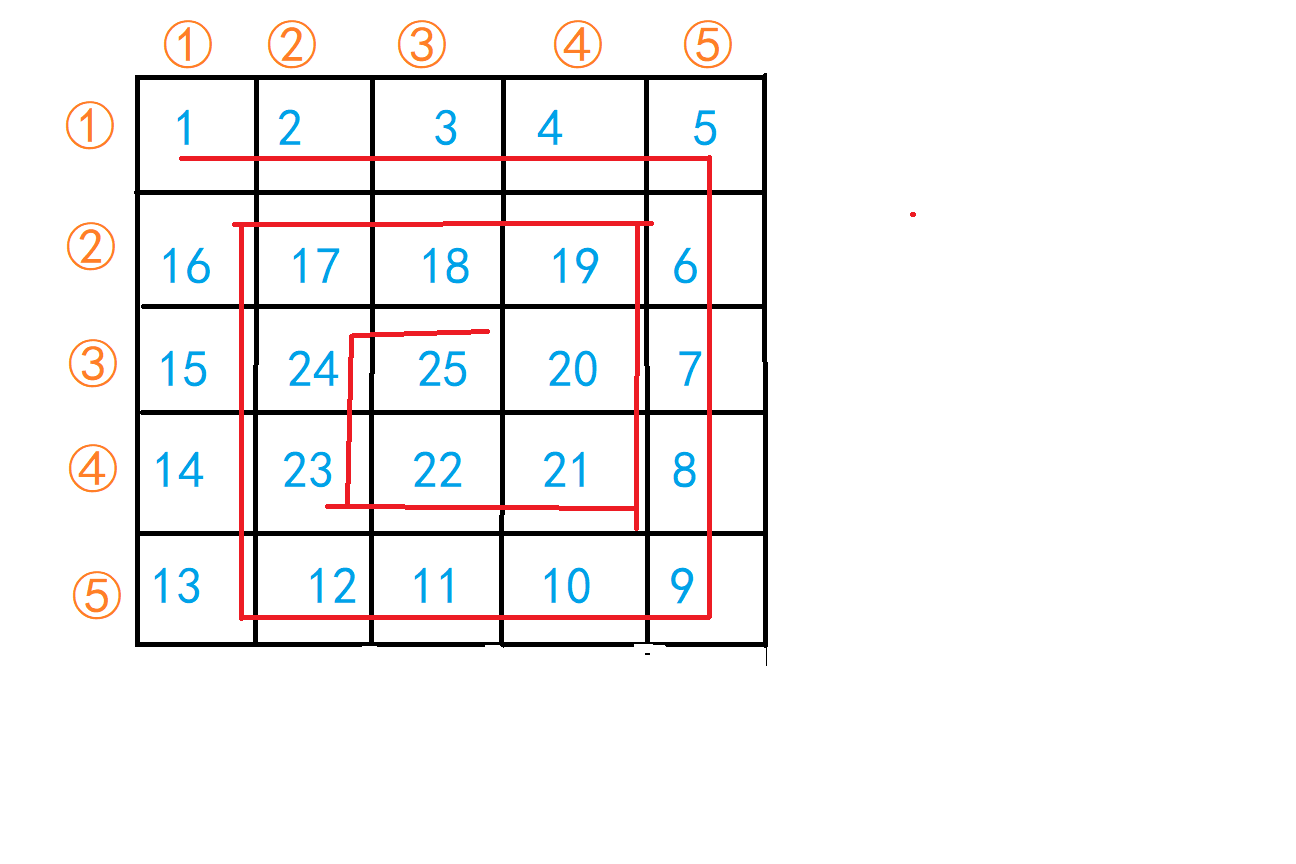
`AcWing` `459`. 螺旋矩阵

解题思路

这道题绝对不能开一个二维数组去一个个模拟，这样空间会爆时间也会超. 这题是一个典型的找规律题目，大家在纸上画图模拟找规律即可。

若n=5,如下图所示

一般这类问题都采用递归解决问题

先思考一下问题的边界有哪些?

i==1
```
if (i == 1) return j;
```

i==n

if (i == n) return 3 * n - j - 1;
// 观察最后一行，找规律：因为最后一行是通过上，右，下到达的
// 上和右是即成事实，也就是2*n-1,而下中其实是取反：n-j,总的来说就是：
// 3*n - j -1

j==1

if (j == 1) return 4 * n - i - 2;
//参考上面的解释，同理推出是4*n-i-2,2就是因为第一行最后一列，最后一行最后一列是重复了2次

j==n
```
if (j == n) return n + i - 1;
```

再讨论一下两个轮次之间的转化关系是什么？

这里所说的轮次，就是矩阵的一圈,怎么个转换法呢？其实，我们是从外到内进搜索的，所以，在搜索内部圈时，外部圈已经完成搜索。但由于4个角有重叠，所以就是4*(n-1)。

对于外圈边长是n的为例，内圈就是n-2,(因为上下左右都是占用了两个嘛~)

那(i,j)有什么变化呢？那当然就是(i-1,j-1)了~

Q:为什么要选择这个的边界做为递归边界？ 答：因为这样好计算，能把大问题转化为小问题后，导向这些边界，获取结果。

`Code`

#include <bits/stdc++.h>
using namespace std;

// 推规律，1行j列为j，n行j列为3n-j-1，1行i列为4n-i-2，n行i列为n+i-1。
int dfs(int n, int i, int j) {
    if (i == 1) return j;
    if (i == n) return 3 * n - j - 1;
    if (j == 1) return 4 * n - i - 2;
    if (j == n) return n + i - 1;
    return dfs(n - 2, i - 1, j - 1) + (n - 1) * 4;
}

int main() {
    int n, a, b;
    cin >> n >> a >> b;
    cout << dfs(n, a, b) << endl;
    return 0;
}

2.3 KiB Raw Blame History Unescape Escape

AcWing 459. 螺旋矩阵