python

4.8 KiB

Raw Blame History Unescape Escape

This file contains ambiguous Unicode characters that may be confused with others in your current locale. If your use case is intentional and legitimate, you can safely ignore this warning. Use the Escape button to highlight these characters.

##AcWing 1309. 车的放置

一、题目描述

有下面这样的一个网格棋盘，a,b,c,d 表示了对应边长度，也就是对应格子数。

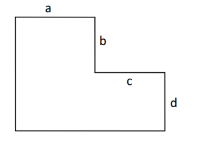
当 a=b=c=d=2 时，对应下面这样一个棋盘：

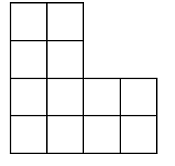
要在这个棋盘上放 k 个相互不攻击的车，也就是这 k 个车没有两个车在同一行，也没有两个车在同一列，问有多少种方案。

只需要输出答案 mod 100003 后的结果。

输入格式 共一行，五个非负整数 a,b,c,d,k。

输出格式 包括一个正整数，为答案 mod 100003 后的结果。

数据范围 0≤a,b,c,d,k≤1000，保证至少有一种可行方案。

输入样例：

2 2 2 2 2

输出样例：

二、算法分析

样例理解

我们可以尝试在每一个空格上放上车，然后躲开同行+同列，会发现有很多种放法，并且要注意不能重复，最后加在一起共38种摆放方案。

1、规则的图形

题目给定的图片是不规则图形，我们可以将它分解成若干个规则图形，因为规则图形可以通过公式直接计算出来，如上图所示，对于某个规则的矩形，长度是b，宽度是a，放 k 辆车（k <= a,k<= b），在长度是b行中任选k行进行摆放，一共有\displaystyle C_b^k \times P_a^k种摆放方案

解释:\displaystyle C_b^k \times P_a^k : 从b行中选择k行，这个很好理解，那为什么是P_a^k呢？如下图：

2、分解图形

（按照红线位置划分成两个矩形）

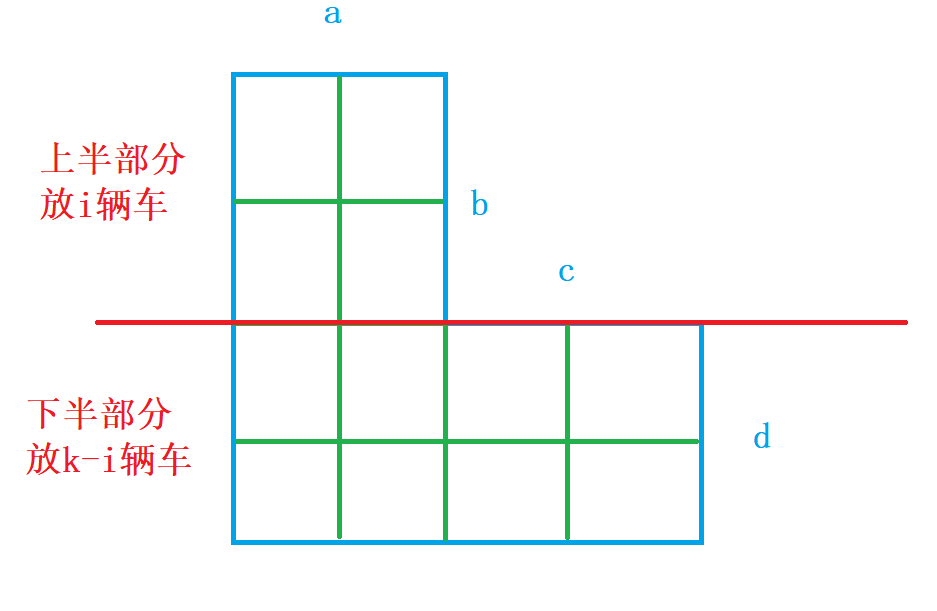
上半部分摆放i辆车，有\displaystyle C_b^i\times P_a^i种摆放方案

下半部分摆放k - i辆车，由于上半部分摆放了i辆车，占用的列对下半部分选择有了一定的影响，即占用的列对于下半部分是不可使用的，因此从d行中选k - i行，有a + c - i列可以进行摆放并摆放k - i辆车，因此有 C_d^{k-i}\times P_{a+c-i}^{k-i} 种摆放方案。

内部是乘法原理，因为后面的结果会受到前面的影响。

乘法原理：理解为一个事件需要经历多个步骤，每个步骤有若干选择，最终的总选择数就是各个步骤选择数的乘积。

上半部分摆放i辆车，整张图的摆放方案是

\large C_b^{i}\times P_a^i \times C_d^{k-i}\times P_{a+c-i}^{k-i}

三、实现代码

组合数公式专题

#include <bits/stdc++.h>
using namespace std;
#define int long long
#define endl "\n"

const int N = 2010, mod = 100003; // 因为式子中出现a+c，所以N要开两倍

int fact[N], infact[N]; // 阶乘与阶乘的逆元

// 快速幂模板
int qmi(int a, int k) {
    int res = 1;
    while (k) {
        if (k & 1) res = res * a % mod;
        a = a * a % mod;
        k >>= 1;
    }
    return res;
}

// 组合数
int C(int a, int b) {
    if (a < b) return 0;
    return fact[a] % mod * infact[a - b] % mod * infact[b] % mod;
}

// 排列数
int P(int a, int b) {
    if (a < b) return 0;
    return fact[a] % mod * infact[a - b] % mod;
}

signed main() {
    // 组合数公式II
    // 预处理出阶乘和阶乘的逆元
    fact[0] = infact[0] = 1; // 0的阶乘是1,这是人为的规定。 1/1也是1，infact[0]也是1
    for (int i = 1; i < N; i++) {
        fact[i] = fact[i - 1] * i % mod;                   // 阶乘
        infact[i] = infact[i - 1] * qmi(i, mod - 2) % mod; // 因为100003是质数，可以用费马小定理求出阶乘的逆元
    }

    int a, b, c, d, k;
    cin >> a >> b >> c >> d >> k;

    int res = 0;
    for (int i = 0; i <= k; i++) // 在上面的矩阵中，放i个，但要注意C(a,b),P(a,b)中a>=b,这里处理的也非常巧妙，
                                 // 没有在计算时进行特判，而是在实现C函数、P函数时进行了特判，if(a<b) return 0;
        res = (res + C(b, i) * P(a, i) % mod * C(d, k - i) % mod * P(a + c - i, k - i)) % mod;

    printf("%lld\n", res);
}

4.8 KiB Raw Blame History Unescape Escape