python

15 KiB

Raw Blame History Unescape Escape

This file contains invisible Unicode characters that may be processed differently from what appears below. If your use case is intentional and legitimate, you can safely ignore this warning. Use the Escape button to reveal hidden characters.

This file contains ambiguous Unicode characters that may be confused with others in your current locale. If your use case is intentional and legitimate, you can safely ignore this warning. Use the Escape button to highlight these characters.

矩阵乘法与矩阵快速幂

一、矩阵的定义

一个 m\times n 的矩阵就是 m 行 n 列的数字阵列,如2 \times 3的矩阵：$\begin{bmatrix} 1 & 5 & 3 \ 2 & 8 & 10 \end{bmatrix}$

实际上，矩阵类似二维数组。

2. 矩阵的运算

矩阵的加法和减法 矩阵的加法和减法就是将两个矩阵对应位置上的数相加减。因此，相加减的两个矩阵A，B的行列必须相同。
矩阵乘法 A，B，C 是三个矩阵，若 A\times B=C，需要满足：
A 的列数必须和 B 的行数相等；
设 A 是一个 n\times r 的矩阵，B 是一个 r\times m 的矩阵，则矩阵 A 乘矩阵 B 的乘积 C 是一个 n\times m 的矩阵；
C_{(i,j)} =A_{(i,1)} ×B_{(1,j)} +A_{(i,2)}×B_{(2,j)} +...A_{(r,1)} ×B_{(r,j)} 矩阵 C 的第 i 行第 j 列元素 = 矩阵 A 的第 i 行元素与矩阵 B的第 j 列对应元素乘积之和。

例如：$A= \begin{bmatrix} a & b \ c & d \ e & f \end{bmatrix}, B= \begin{bmatrix} g & h & i \ j & k & l \end{bmatrix},求$C=A \times B

$A \times B=\begin{bmatrix} a \times g+b \times j & a \times h+b \times k & a \times i + b \times l \ c \times g+d \times j & c \times h+d \times k & c \times i + d \times l \ e \times g+f \times j & e \times h+f \times k & e \times i + f \times l \end{bmatrix}$

可以发现 A\times B 和 B\times A 将得到两种不同的结果，因此矩阵不满足乘法交换律。

方阵次幂 如果矩阵的行和列相同，称矩阵为方阵。若 A 是一个方阵，方阵的幂是指，将 A 连乘 n 次，A^n。

若不是方阵则无法进行乘幂运算。

矩阵乘法不满足交换律，但是满足结合律，因此可以用快速幂的思想来求解方程次幂。

3. 矩阵乘法的应用

在信息学竞赛中考矩阵乘法不是为了考基本运算，而是利用矩阵乘法的特性，配合快速幂求解递推式的第 n 项，以及一些图论的构造转化。

一本通 1641 矩阵乘法

B2105 矩阵乘法

注释：上面两道题其实是一样的模板，只不过输入的数据顺序不太一样。

#include <bits/stdc++.h>
using namespace std;
const int N = 110;
int n, m, k;
int a[N][N], b[N][N], c[N][N];

// 矩阵乘法模板
void mul(int a[][N], int b[][N], int c[][N]) {
    // 注意：这里的临时数组t绝不是画蛇添足！
    // 因为调用的时候，有时会传递mul(a,b,b)这样的东东，如果每次memset(c,0,sizeof c),
    // 就会造成b在运行前被清空，导致结果错误

    // 代码解释:
    // 从结果出发理解：
    // C(i,j) =A(i,1)×B(1,j)+A(i,2)×B(2,j) +...A(r,1)×B(r,j)
    // 抽象一下：
    // C(i,j) = C(i,j) + A(i,k)× B(k,j)
    int t[N][N] = {0};
    for (int i = 0; i < N; i++)
        for (int j = 0; j < N; j++)
            for (int k = 0; k < N; k++)
                t[i][j] = t[i][j] + a[i][k] * b[k][j]; // 矩阵乘法
    memcpy(c, t, sizeof t);
}
int main() {
    cin >> n >> m >> k;

    // A矩阵 n*m
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= m; j++)
            cin >> a[i][j];

    // B矩阵m*k
    for (int i = 1; i <= m; i++)
        for (int j = 1; j <= k; j++)
            cin >> b[i][j];

    // 矩阵乘法
    mul(a, b, c);

    // 输出结果，控制格式
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= k; j++)
            printf("%d ", c[i][j]);
        printf("\n");
    }

    return 0;
}

P3390 【模板】矩阵快速幂

快速幂 实现 pow(x, n) ，即计算 x 的整数 n 次幂函数 (即x^n)。

对于上面这道题，我们最容易想到的解法就是通过循环或递归进行累乘求解

public double MyPow(double x, int n){
	long N = n;
	if (N == 0) return 1;
	double res = x;
	long num = N > 0 ? N : -N;
	for (long i = 1; i < num; i++){
		res *= x;
	}
	if (N < 0) res = 1 / res;
	return res;
}

然而，这种解法在面对n比较大的情况时，效率会变得十分低下。仔细想想上面的循环过程就会发现，里面进行了很多次无意义的计算。以a^{10} 举例，通过循环一个一个往上乘，需要进行9次运算。而如果我们先计算出a^2 （1次），然后计算a^2*a^2*a^2*a^2*a^2 （4次），总计算量就能减少到5次。如果先计算出a^4（2次），再计算a^2*a^4*a^4（2次），总计算量就能减少到4次。

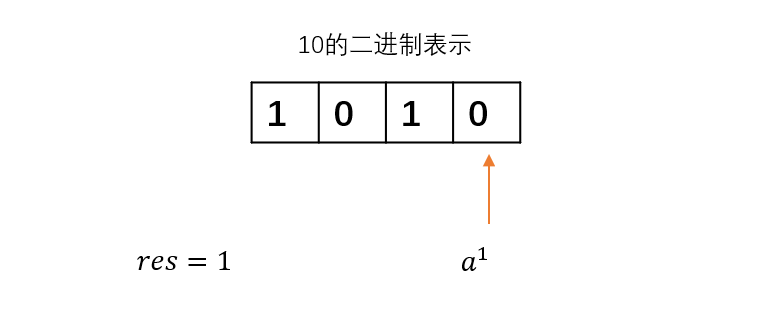
也就是说，将a^n 拆解成a^x*a^y*a^z...的形式就可以降低总体运算的次数。那么如何拆解n才最高效呢？根据前面的思路，显然是每次平方所需的运算次数最少。仍然是a^{10} 的例子，我们从a^1 开始，每次取平方值，可以得到[a^1,a^2,a^4,a^8]。想要组成a^{10} ，只需要让a^8*a^2 即可。所需的计算次数也是4次。看到这里有没有觉得熟悉？我们实际上就是在把n拆成几个2^?相加，也就是类似于n的二进制转换成十进制的过程。

下面仍然以a^{10} 为例，通过图展示一下计算过程：我们从10的最低位开始遍历，遇到的第一位是0，对应的是a^1 ，但我们并不需要它计算结果，所以跳过。

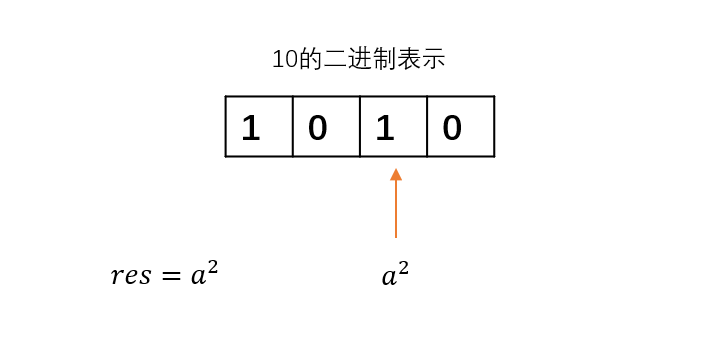
接下来遇到的第二位是1，对应a^2 ，这是计算结果需要用到的，所以把它乘到res上。继续移动指针。

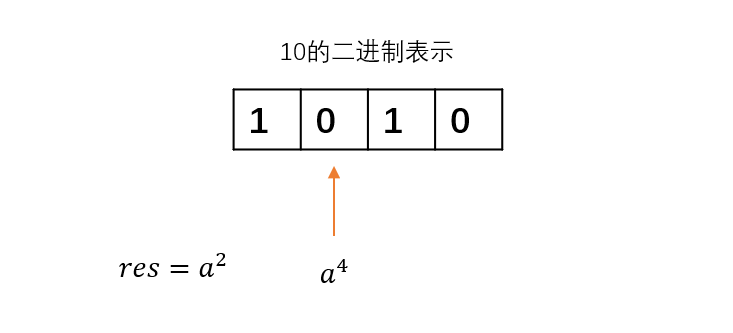
遇到的第三位是0，对应a^4 ，用不到，跳过。

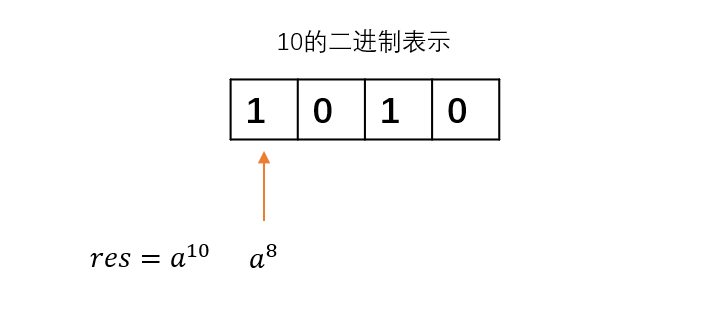
遇到的第四位是1，对应a^8 ，需要用到，把它乘到res中。

res便是最终结果。将上面的思路转换成代码（未考虑特殊情况）：

double pow(double a, int n){
	double res = 1;
	while (n){
		// 当前位为1,计入结果
		if ((n & 1) == 1) res = res * a;
		// a自乘
		a *= a;
		// n右移
		n >>= 1;
	}
	return res;
}

单位矩阵

在普通的乘法中，一个数乘1还是等于它本身，在矩阵乘法中也有这么一个1，它就是 单位矩阵

不同于普通乘法中的单位1，对于不同矩阵他们的单位矩阵大小是不同的

对于n∗m的矩阵，它的单位矩阵大小为m∗m，对于m∗n的矩阵，它的单位矩阵大小为n∗n

也就是说单位矩阵都是正方形的，这是因为只有正方形的矩阵能保证结果和前一个矩阵形状相同

单位矩阵的元素非0即1，从左上角到右下角的对角线上元素皆为1，其他皆为0

矩阵快速幂-(单位矩阵)

#include <bits/stdc++.h>
using namespace std;
#define int long long
#define endl "\n"
const int MOD = 1e9 + 7;
const int N = 110;
int n, k;             // 本题数据范围很大，用int直接wa哭了
int a[N][N], b[N][N]; // 原始矩阵，结果矩阵

// 矩阵乘法模板
void mul(int a[][N], int b[][N], int c[][N]) {
    int t[N][N] = {0};
    for (int i = 0; i < N; i++)
        for (int j = 0; j < N; j++)
            for (int k = 0; k < N; k++)
                t[i][j] = (t[i][j] + a[i][k] * b[k][j] % MOD) % MOD; // 矩阵乘法
    memcpy(c, t, sizeof t);
}

signed main() {
    cin >> n >> k;
    // 输入原始矩阵
    for (int i = 0; i < n; i++)
        for (int j = 0; j < n; j++)
            cin >> a[i][j];

    // 1、单位矩阵
    for (int i = 0; i < n; i++) b[i][i] = 1;

    // 2、矩阵快速幂
    for (int i = k; i; i >>= 1) {
        if (i & 1) mul(a, b, b);
        mul(a, a, a);
    }

    // 3、输出
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < n; j++)
            printf("%lld ", b[i][j]);
        printf("\n");
    }
}

矩阵快速幂-(不使用单位矩阵)

#include <bits/stdc++.h>
using namespace std;
#define int long long
#define endl "\n"
const int MOD = 1e9 + 7;
const int N = 110;
int n, k;             // 本题数据范围很大，用int直接wa哭了
int a[N][N], b[N][N]; // 原始矩阵，结果矩阵

// 矩阵乘法
void mul(int a[][N], int b[][N], int c[][N]) {
    int t[N][N] = {0};
    for (int i = 0; i < N; i++)
        for (int j = 0; j < N; j++)
            for (int k = 0; k < N; k++)
                t[i][j] = (t[i][j] + a[i][k] * b[k][j] % MOD) % MOD; // 矩阵乘法
    memcpy(c, t, sizeof t);
}

int main() {
    cin >> n >> k;
    // 1、输入原始矩阵
    for (int i = 0; i < n; i++)
        for (int j = 0; j < n; j++) {
            cin >> a[i][j];
            b[i][j] = a[i][j]; // 这种解法与标准解法不同，不用构建单位矩阵
            // 直接赋值初始化了一个，然后执行k-1次就完成了矩阵的k次幂
        }

    // 2、计算矩阵快速幂
    for (int i = k - 1; i; i >>= 1) {
        if (i & 1) mul(a, b, b);
        mul(a, a, a);
    }

    // 3、输出
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < n; j++)
            printf("%lld ", b[i][j]);
        printf("\n");
    }

    return 0;
}

理解：不管是用单位矩阵也好，不用单位矩阵也罢，本质上都是类似于构造一个乘法的基底：数字1！

矩阵快速幂应用：斐波那契数列

矩阵快速幂的一个非常典型的应用就是斐波那契数列（原题地址）。先来看斐波那契数列的定义：

F(1)=0,F(2)=1

F(n)=F(n-1)+F(n-2),其中n>1

我们先定义一个矩阵

b=\begin{bmatrix} F(n) & F(n-1) \end{bmatrix}

现在假设有一个变换矩阵M，与上述矩阵存在如下关系

\begin{bmatrix}F(n) & F(n-1) \end{bmatrix} \times M= \begin{bmatrix}F(n+1) & F(n) \end{bmatrix}

很显然，M是一个2×2的矩阵，我们假设

M=\begin{bmatrix}
a & b \\ 
c & d
\end{bmatrix}$$

带入上面的公式可得
$\begin{bmatrix}F(n)& F(n-1)\end{bmatrix} \times
\begin{bmatrix}a& b \\
c & d \\
\end{bmatrix}=\begin{bmatrix}
aF(N)+cF(n-1)&  bF(n)+dF(n-1)
\end{bmatrix} =
\begin{bmatrix} F(n+1)& F(n) \end{bmatrix}$


也就是
$$aF(n)+cF(n-1)=F(n+1)$$
$$bF(n)+dF(n-1)=F(n)$$

依照$Fibonacci$的现实含义，很容易得出
$$M=\begin{bmatrix}
1 & 1 \\ 
1 & 0
\end{bmatrix}$$

即
$$\begin{bmatrix} F(n) & F(n-1) \end{bmatrix} \times 
\begin{bmatrix} 1 & 1 \\
1 & 0
\end{bmatrix}=\begin{bmatrix} F(n+1) & F(n) \end{bmatrix} \ ①$$ 


同理
$$\begin{bmatrix} F(n-1) & F(n-2) \end{bmatrix} \times 
\begin{bmatrix} 1 & 1 \\
1 & 0
\end{bmatrix}=\begin{bmatrix} F(n) & F(n-1) \end{bmatrix} \ ②$$ 

将 ② 代入 ①,得
$$\begin{bmatrix}F(n+1) & F(n) \end{bmatrix} = 
\begin{bmatrix}F(n-1) & F(n-2) \end{bmatrix} \times \begin{bmatrix}
1 & 1 \\ 
1 & 0 
\end{bmatrix} ^{2}$$

根据数学归纳法:
$\begin{bmatrix} F(n-1)& F(n-2) \end{bmatrix}$ 与$M$矩阵的平方匹配.也就是$F(n-1)$中$n-1+2=n+1$，一路递推上去，就是

$$\begin{bmatrix}F(n+1) & F(n) \end{bmatrix} = 
\begin{bmatrix}F(2) & F(1) \end{bmatrix} \times \begin{bmatrix}
1 & 1 \\ 
1 & 0 
\end{bmatrix} ^{n-1}$$

我们只需要定义出矩阵乘法，配合前面的快速幂，即可实现在$O(logN)$时间复杂度内解出斐波那契数列。




**[$YBT$_$1642$ $Fibonacci$ 第 $n$ 项](https://www.cnblogs.com/littlehb/p/17074586.html)**
```cpp {.line-numbers}
#include <bits/stdc++.h>

using namespace std;
const int INF = 0x3f3f3f3f;
#define int long long
#define endl "\n"
/*
http://ybt.ssoier.cn:8088/problem_show.php?pid=1642
测试用例：
5 1000

答案：
5
*/
const int N = 2;

int n, mod;

// 矩阵乘法
void mul(int a[][N], int b[][N], int c[][N]) {
    int t[N][N] = {0};
    for (int i = 0; i < N; i++) {
        for (int j = 0; j < N; j++)
            for (int k = 0; k < N; k++)
                t[i][j] = (t[i][j] + (a[i][k] * b[k][j]) % mod) % mod;
    }
    memcpy(c, t, sizeof t);
}

signed main() {
    cin >> n >> mod;

    int b[N][N] = {1, 1}; // 结果矩阵(初始化fib[2]=1,fib[1]=1)

    // 构造的向量数组
    int m[N][N] = {
        {1, 1},
        {1, 0}};

    // 矩阵快速幂
    for (int i = n - 1; i; i >>= 1) {
        if (i & 1) mul(b, m, b);
        mul(m, m, m);
    }

    printf("%lld\n", b[0][1]);
    return 0;
}
```
> **$Q_1$**：为什么在计算矩阵快速幂时提出了一个单元矩阵的概念，而在上面的斐波那契第$n$项中，却没有使用单元矩阵呢？什么时候用单元矩阵，什么时候不用呢？
> **答**：不管是单元矩阵组装出的$1$的概念基底，还是默认把$1$次方做为基底,都是希望有一个**基底**,斐波那契数列这道题中，由于有$b[2],b[1]$组成的初始值，构成了一个 **基底** 矩阵,所以，就可以直接使用这引基底矩阵一路乘上去就行了。

>**$Q_2$: $b[0],b[1]$明明是一维数组，或者叫只有一行的矩阵，为什么还要声明为 $b[N][N]$呢？**
> **答**：是因为我懒！因为我懒得要写两个矩阵乘法的模板，也懒得背两个矩阵乘法的模板！是哪两个呢？
> - 二维乘一维
> - 二维乘二维
> 我整理的模板就是二维乘二维的，没有整理二维乘一维，或者，一维乘二维的。因为二维乘二维可以模拟出二维乘一维的：对于一维矩阵，只需要初始化第一行的所有数据，其它数据为$0$，就可以模拟出二维乘一维的效果了。

>**$Q_3$：$b$数组的含义是什么呢？**
**答**：其实$b$矩阵是构造出来的，表现形式是$b=[F(n) \  F(n-1)]$,按题目的意思，$Fibonacci$数列是从下标$1$开始的,$f_1=f_2=1$,所以$b$的初始值就是$[F(2) \  F(1)]$

**[$AcWing$ $1303$. 斐波那契前 $n$ 项和](https://www.cnblogs.com/littlehb/p/16341964.html)**
相比于上一道题，本题增加了一个概念$S_n$,含义是前$n$个$f_n$的和,难度有所增加。


**[$P1939$ 矩阵加速（数列）](https://www.cnblogs.com/littlehb/p/16039658.html)**


**[$AcWing$ $1304$. 佳佳的斐波那契](https://www.cnblogs.com/littlehb/p/16342848.html)** 


**[$AcWing$ $1305$. $GT$考试](https://www.cnblogs.com/littlehb/p/16348443.html)**


https://blog.csdn.net/STRVE/article/details/106739349

15 KiB Raw Blame History Unescape Escape

矩阵乘法与矩阵快速幂

一、矩阵的定义

2. 矩阵的运算

3. 矩阵乘法的应用

15 KiB

Raw Blame History Unescape Escape