|
|
## [$AcWing$ $1134$. 最短路计数](https://www.acwing.com/problem/content/1136/)
|
|
|
|
|
|
### 一、题目描述
|
|
|
给出一个 $N$ 个顶点 $M$ 条边的 **无向无权图**,顶点编号为 $1$ 到 $N$。
|
|
|
|
|
|
问从顶点 $1$ 开始,到其他每个点的 **最短路有几条**。
|
|
|
|
|
|
**输入格式**
|
|
|
第一行包含 $2$ 个正整数 $N,M$,为图的顶点数与边数。
|
|
|
|
|
|
接下来 $M$ 行,每行两个正整数 $x,y$,表示有一条顶点 $x$ 连向顶点 $y$ 的边,**请注意可能有自环与重边**。
|
|
|
|
|
|
**输出格式**
|
|
|
输出 $N$ 行,每行一个非负整数,第 $i$ 行输出从顶点 $1$ 到顶点 $i$ 有多少条不同的最短路,由于答案有可能会很大,你只需要输出对 $100003$ 取模后的结果即可。
|
|
|
|
|
|
如果无法到达顶点 $i$ 则输出 $0$。
|
|
|
|
|
|
**数据范围**
|
|
|
$1≤N≤105,1≤M≤2×10^5$
|
|
|
|
|
|
**输入样例**:
|
|
|
```cpp {.line-numbers}
|
|
|
5 7
|
|
|
1 2
|
|
|
1 3
|
|
|
2 4
|
|
|
3 4
|
|
|
2 3
|
|
|
4 5
|
|
|
4 5
|
|
|
```
|
|
|
|
|
|
**输出样例**:
|
|
|
```cpp {.line-numbers}
|
|
|
1
|
|
|
1
|
|
|
1
|
|
|
2
|
|
|
4
|
|
|
```
|
|
|
|
|
|
### 二、解题思路
|
|
|
|
|
|
> 要求 **最短路计数** 要满足: **不能存在路径和为$0$的环**,因为存在的话某个环中不断的转圈不出来,而路径长度不变,那么被更新的点的条数就为$INF$了
|
|
|
|
|
|
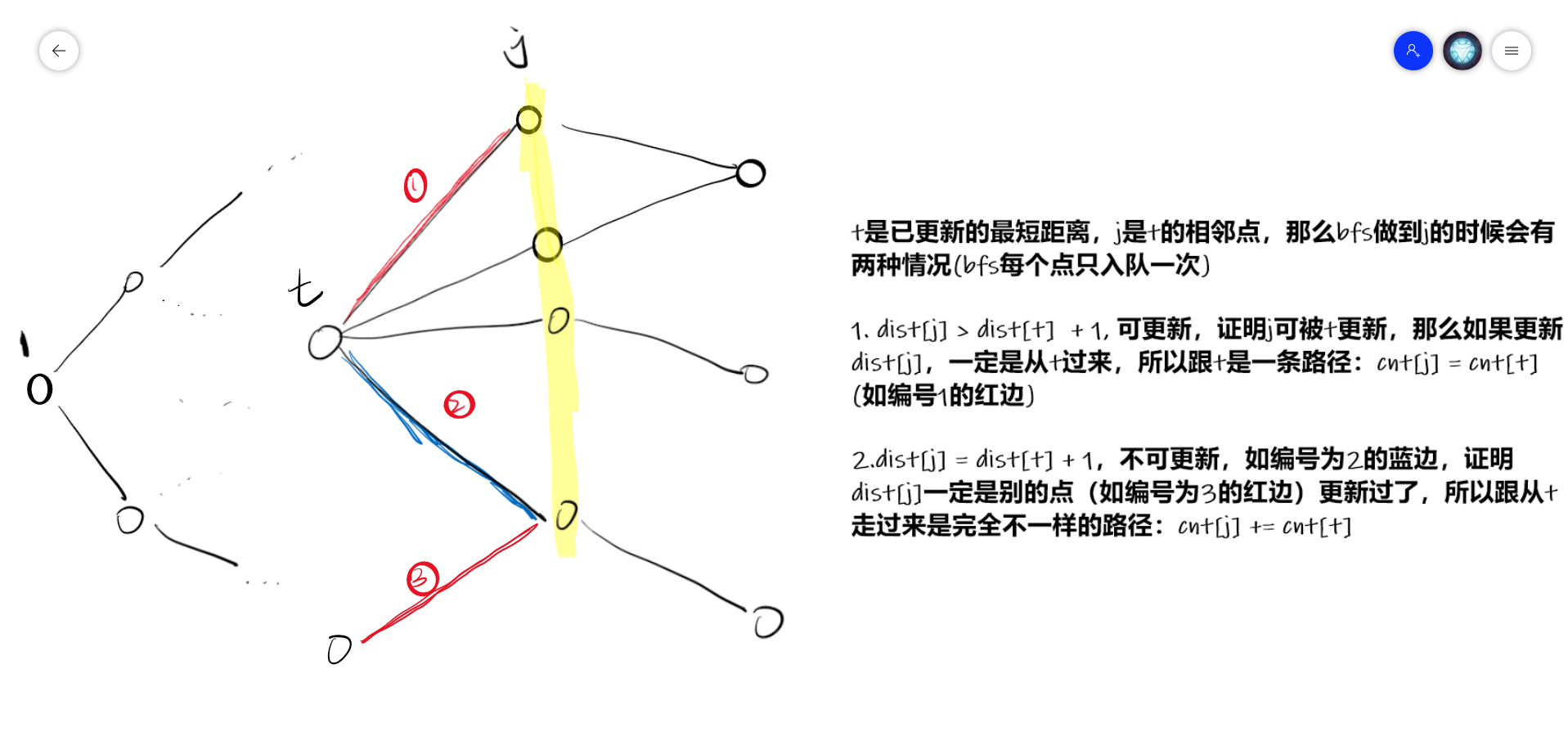
#### 1. 更新记录最短路的数量
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
#### 2. 求最短路的算法
|
|
|
* $bfs$
|
|
|
只入队一次,出队一次, **可以抽象成拓扑图**, 因为它可以保证被更新的点的父节点一定已经是最短距离了,并且这个点的条数已经被完全更新过了。
|
|
|
|
|
|
* $dijkstra$
|
|
|
每个点只出队一次, **可以抽象成拓扑图**, 同理由于每一个出队的点 **一定** 已经是 **最短距离**,并且它出队的时候是队列中距离最小的点,这就代表他的最短距离条数已经被完全更新了,所以构成拓扑性质。
|
|
|
|
|
|
|
|
|
<!-- 让表格居中显示的风格 -->
|
|
|
<style>
|
|
|
.center
|
|
|
{
|
|
|
width: auto;
|
|
|
display: table;
|
|
|
margin-left: auto;
|
|
|
margin-right: auto;
|
|
|
}
|
|
|
</style>
|
|
|
<div class="center">
|
|
|
|
|
|
| 题型 | 方法 | 可行性 | 备注 |
|
|
|
| ----------------------------------- | -------------------------------- | ------ | --------------------------------------------- |
|
|
|
| 最短路+最短路数量 | $Dijkstra+Heap+DP$ | $√$ | <font color='red' size='4'><b>推荐</b></font> |
|
|
|
| | $bfs+DP$ | $√$ | 了解 |
|
|
|
| | $spfa+DP$ | $√$ | 了解 |
|
|
|
| | 求最短路+建拓扑图+遍历拓扑图$DP$ | $√$ | <font color='blue' size=4><b> 学习</b></font> |
|
|
|
| 最短路+最短中数量+次短路+次短路数量 | $Dijkstra$堆优化+$DP$+拆点 | $√$ | <font color='red' size=4><b>推荐</b></font> |
|
|
|
| | $bfs+DP$ | $×$ | |
|
|
|
| | $spfa+DP$ | $×$ | |
|
|
|
| | 求最短路+建拓扑图+遍历拓扑图$DP$ | $√$ | <font color='blue' size=4><b>学习</b></font> |
|
|
|
</div>
|
|
|
|
|
|
|
|
|
|
|
|
#### $bfs$解法
|
|
|
```cpp {.line-numbers}
|
|
|
#include <bits/stdc++.h>
|
|
|
using namespace std;
|
|
|
const int N = 4e5 + 10;
|
|
|
const int MOD = 100003;
|
|
|
int h[N], ne[N], e[N], idx;
|
|
|
void add(int a, int b) {
|
|
|
e[idx] = b, ne[idx] = h[a], h[a] = idx++;
|
|
|
}
|
|
|
|
|
|
int cnt[N]; // 从顶点1开始,到其他每个点的最短路有几条
|
|
|
int dis[N]; // 最短距离
|
|
|
int n, m;
|
|
|
void bfs() {
|
|
|
memset(dis, 0x3f, sizeof dis);
|
|
|
queue<int> q;
|
|
|
q.push(1);
|
|
|
cnt[1] = 1; // 从顶点1开始,到顶点1的最短路有1条
|
|
|
dis[1] = 0; // 距离为0
|
|
|
|
|
|
while (q.size()) {
|
|
|
int u = q.front();
|
|
|
q.pop();
|
|
|
for (int i = h[u]; ~i; i = ne[i]) {
|
|
|
int j = e[i];
|
|
|
if (dis[j] > dis[u] + 1) {
|
|
|
dis[j] = dis[u] + 1;
|
|
|
q.push(j);
|
|
|
cnt[j] = cnt[u];
|
|
|
} else if (dis[j] == dis[u] + 1)
|
|
|
cnt[j] = (cnt[j] + cnt[u]) % MOD;
|
|
|
}
|
|
|
}
|
|
|
}
|
|
|
int main() {
|
|
|
memset(h, -1, sizeof h);
|
|
|
scanf("%d %d", &n, &m);
|
|
|
while (m--) {
|
|
|
int a, b;
|
|
|
scanf("%d %d", &a, &b);
|
|
|
add(a, b), add(b, a);
|
|
|
}
|
|
|
bfs();
|
|
|
for (int i = 1; i <= n; i++) printf("%d\n", cnt[i]);
|
|
|
return 0;
|
|
|
}
|
|
|
```
|
|
|
|
|
|
#### $Dijkstra$解法
|
|
|
```cpp {.line-numbers}
|
|
|
#include <bits/stdc++.h>
|
|
|
using namespace std;
|
|
|
typedef pair<int, int> PII;
|
|
|
const int N = 100010, M = 400010;
|
|
|
const int MOD = 100003;
|
|
|
|
|
|
int n, m;
|
|
|
int cnt[N];
|
|
|
int dis[N];
|
|
|
bool st[N];
|
|
|
int h[N], e[M], ne[M], idx;
|
|
|
void add(int a, int b) {
|
|
|
e[idx] = b, ne[idx] = h[a], h[a] = idx++;
|
|
|
}
|
|
|
|
|
|
void dijkstra() {
|
|
|
memset(dis, 0x3f, sizeof dis);
|
|
|
dis[1] = 0;
|
|
|
cnt[1] = 1; // 出发点到自己的最短路径有1条,长度是0
|
|
|
|
|
|
// 小顶堆q
|
|
|
priority_queue<PII, vector<PII>, greater<PII>> q;
|
|
|
q.push({0, 1});
|
|
|
|
|
|
while (q.size()) {
|
|
|
auto t = q.top();
|
|
|
q.pop();
|
|
|
int u = t.second;
|
|
|
|
|
|
if (st[u]) continue;
|
|
|
st[u] = true;
|
|
|
|
|
|
for (int i = h[u]; ~i; i = ne[i]) {
|
|
|
int j = e[i];
|
|
|
if (dis[j] > dis[u] + 1) {
|
|
|
dis[j] = dis[u] + 1;
|
|
|
cnt[j] = cnt[u];
|
|
|
q.push({dis[j], j});
|
|
|
} else if (dis[j] == dis[u] + 1)
|
|
|
cnt[j] = (cnt[j] + cnt[u]) % MOD;
|
|
|
}
|
|
|
}
|
|
|
}
|
|
|
|
|
|
int main() {
|
|
|
scanf("%d %d", &n, &m);
|
|
|
memset(h, -1, sizeof h);
|
|
|
while (m--) {
|
|
|
int a, b;
|
|
|
scanf("%d %d", &a, &b);
|
|
|
add(a, b), add(b, a);
|
|
|
}
|
|
|
dijkstra();
|
|
|
for (int i = 1; i <= n; i++) printf("%d\n", cnt[i]);
|
|
|
return 0;
|
|
|
}
|
|
|
```
|
|
|
|
|
|
|
|
|
### 三、扩展练习
|
|
|
[$POJ$ - $3463$ $Sightseeing$](http://poj.org/problem?id=3463)
|
|
|
|
|
|
**最短路计数+ 次短路计数**
|
|
|
|
|
|
**题意**
|
|
|
已知一张图(单向边),起点$S$和终点$F$,求从 $S $到 $F$ 的 **最短路** 和 **比最短路长$1$** 的路径的 **条数之和**。
|
|
|
|
|
|
**分析**
|
|
|
只需要计算出最短路的条数和距离、次短路的距离和条数,最后判断最短路和次短路的关系即可,在$dijkstra$求最短路的基础上,**加一维** 保存从起点到该点的 **最短路** 和 **次短路**,**同时记录相应的数量**
|
|
|
|
|
|
如果当前点的最短路或次短路更新了,那么这个点可能松弛其他点,加入优先队列;如果等于最短路或次短路,相应的数量就加。
|
|
|
|
|
|
关于代码中①②的自我解释:
|
|
|
|
|
|
①:一个点可能被几个点松弛,每松弛一次就入一次队列,那么这个点也会出几次队列,也就会重复松弛后面的点,路径数量就会算重,所以要标记每个点的最短路和次短路是否出队,所以入队时要记录入队的是最短路还是次短路,再者,这个标记本来具有优化作用,这里求数量又多了一层意义,就不能使用其他的优化方式了
|
|
|
|
|
|
②:为什么当前点的次短路更新为当前点的最短路时,还要入队呢?当前点的最短路被松弛时已经入过队了啊,原因很简单,因为每个点入队时都记录了入队的是最短路,还是次短路,再一次更新最短路时,数量也随之更新,而上一次入队的最短路的数量就不再是自己的数量了,而是更新后最短路的数量
|
|
|
|
|
|
|
|
|
```cpp {.line-numbers}
|
|
|
#include <queue>
|
|
|
#include <cstring>
|
|
|
#include <iostream>
|
|
|
#include <algorithm>
|
|
|
using namespace std;
|
|
|
#define x first
|
|
|
#define y second
|
|
|
|
|
|
const int N = 1e3 + 13;
|
|
|
const int M = 1e6 + 10;
|
|
|
int n, m, u, v, s, f;
|
|
|
// 将最短路扩展为二维,含义:最短路与次短路
|
|
|
// dis:路径长度,cnt:路线数量,st:是否已经出队列
|
|
|
int dis[N][2], cnt[N][2];
|
|
|
bool st[N][2];
|
|
|
|
|
|
// 链式前向星
|
|
|
int e[M], h[N], idx, w[M], ne[M];
|
|
|
void add(int a, int b, int c = 0) {
|
|
|
e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx++;
|
|
|
}
|
|
|
|
|
|
struct Node {
|
|
|
// u: 节点号
|
|
|
// d:目前结点v的路径长度
|
|
|
// k:是最短路0还是次短路1
|
|
|
int u, d, k;
|
|
|
const bool operator<(Node x) const {
|
|
|
return d > x.d;
|
|
|
}
|
|
|
};
|
|
|
|
|
|
void dijkrsta() {
|
|
|
priority_queue<Node> q; // 默认是大顶堆,通过定义结构体小于号,实现小顶堆。比如:认证的d值更大,谁就更小!
|
|
|
memset(dis, 0x3f, sizeof dis); // 清空最小距离与次小距离数组
|
|
|
memset(cnt, 0, sizeof cnt); // 清空最小距离路线个数与次小距离路线个数数组
|
|
|
memset(st, 0, sizeof st); // 清空是否出队过数组
|
|
|
|
|
|
cnt[s][0] = 1; // 起点s,0:最短路,1:有一条
|
|
|
cnt[s][1] = 0; // 次短路,路线数为0
|
|
|
|
|
|
dis[s][0] = 0; // 最短路从s出发到s的距离是0
|
|
|
dis[s][1] = 0; // 次短路从s出发到s的距离是0
|
|
|
|
|
|
q.push({s, 0, 0}); // 入队列
|
|
|
|
|
|
while (q.size()) {
|
|
|
Node x = q.top();
|
|
|
q.pop();
|
|
|
|
|
|
int u = x.u, k = x.k; // u:节点号,k:是最短路还是次短路,d:路径长度(这个主要用于堆中排序,不用于实战,实战中可以使用dis[u][k])
|
|
|
|
|
|
if (st[u][k]) continue; // ① 和dijkstra标准版本一样的,只不过多了一个维度
|
|
|
st[u][k] = true;
|
|
|
|
|
|
for (int i = h[u]; ~i; i = ne[i]) {
|
|
|
int j = e[i];
|
|
|
int dj = dis[u][k] + w[i]; // 原长度+到节点j的边长
|
|
|
|
|
|
if (dj == dis[j][0]) // 与到j的最短长度相等,则更新路径数量
|
|
|
cnt[j][0] += cnt[u][k];
|
|
|
else if (dj < dis[j][0]) { // 找到更小的路线,需要更新
|
|
|
dis[j][1] = dis[j][0]; // 次短距离被最短距离覆盖
|
|
|
cnt[j][1] = cnt[j][0]; // 次短个数被最短个数覆盖
|
|
|
|
|
|
dis[j][0] = dj; // 更新最短距离
|
|
|
cnt[j][0] = cnt[u][k]; // 更新最短个数
|
|
|
|
|
|
q.push({j, dis[j][1], 1}); // ②
|
|
|
q.push({j, dis[j][0], 0});
|
|
|
} else if (dj == dis[j][1]) // 如果等于次短
|
|
|
cnt[j][1] += cnt[u][k]; // 更新次短的方案数,累加
|
|
|
else if (dj < dis[j][1]) { // 如果大于最短,小于次短,两者中间
|
|
|
dis[j][1] = dj; // 更新次短距离
|
|
|
cnt[j][1] = cnt[u][k]; // 更新次短方案数
|
|
|
q.push({j, dis[j][1], 1}); // 次短入队列
|
|
|
}
|
|
|
}
|
|
|
}
|
|
|
}
|
|
|
int main() {
|
|
|
#ifndef ONLINE_JUDGE
|
|
|
freopen("POJ3463.in", "r", stdin);
|
|
|
/*
|
|
|
答案:
|
|
|
3
|
|
|
2
|
|
|
*/
|
|
|
#endif
|
|
|
int T;
|
|
|
scanf("%d", &T);
|
|
|
while (T--) {
|
|
|
memset(h, -1, sizeof h);
|
|
|
scanf("%d %d", &n, &m);
|
|
|
while (m--) {
|
|
|
int a, b, c;
|
|
|
scanf("%d %d %d", &a, &b, &c);
|
|
|
add(a, b, c);
|
|
|
}
|
|
|
// 起点和终点
|
|
|
scanf("%d %d", &s, &f);
|
|
|
// 计算最短路
|
|
|
dijkrsta();
|
|
|
// 输出
|
|
|
printf("%d\n", cnt[f][0] + (dis[f][1] == dis[f][0] + 1 ? cnt[f][1] : 0));
|
|
|
}
|
|
|
return 0;
|
|
|
}
|
|
|
|
|
|
```
|