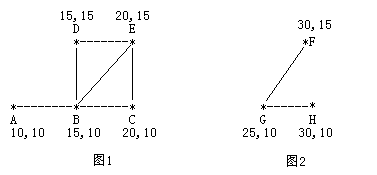8.5 KiB
AcWing 1125 牛的旅行
一、题目描述
农民John的农场里有很多 牧区，有的路径连接一些特定的 牧区。
一片所有 连通的牧区 称为一个 牧场。
但是就目前而言，你能看到至少有两个牧区不连通。
现在，John想在农场里 添加一条路径（注意，恰好一条）。
一个牧场的直径就是牧场中最远的两个牧区的距离（本题中所提到的所有距离指的都是 最短的距离）。
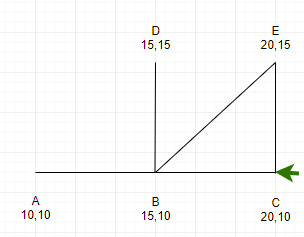
考虑如下的两个牧场，每一个牧区都有自己的坐标：
图 1 是有 5 个牧区的牧场，牧区用 * 表示，路径用直线表示。
图 1 所示的牧场的直径大约是 12.07106, 最远的两个牧区是 A 和 E，它们之间的最短路径是 A-B-E。
图 2 是另一个牧场。
这两个牧场都在John的农场上。
John将会在两个牧场中各选一个牧区，然后用一条路径连起来，使得连通后这个新的更大的牧场有最小的直径。
注意，如果两条路径中途相交，我们不认为它们是连通的。
只有两条路径在同一个牧区相交，我们才认为它们是连通的。
现在请你编程找出一条连接两个不同牧场的路径，使得连上这条路径后，所有牧场（生成的新牧场和原有牧场）中直径最大的牧场的直径尽可能小。
输出这个直径最小可能值。
输入格式
第 1 行：一个整数 N, 表示牧区数；
接下来
N行，每行N个数字，代表邻接矩阵M。第i行第j列的数字为1，表示i号牧区和j号牧区之间存在一条道路直接相连；第i行第j列的数字为0，表示i号牧区和j号牧区之间不存在直接相连的道路。
第 2 到 N+1 行：每行两个整数 X,Y， 表示 N 个牧区的坐标。每个牧区的坐标都是不一样的。
第 N+2 行到第 2*N+1 行：每行包括 N 个数字 ( 0或1 ) 表示一个对称邻接矩阵。
例如，题目描述中的两个牧场的矩阵描述如下：
A B C D E F G H
A 0 1 0 0 0 0 0 0
B 1 0 1 1 1 0 0 0
C 0 1 0 0 1 0 0 0
D 0 1 0 0 1 0 0 0
E 0 1 1 1 0 0 0 0
F 0 0 0 0 0 0 1 0
G 0 0 0 0 0 1 0 1
H 0 0 0 0 0 0 1 0
输入数据中至少包括两个不连通的牧区。
输出格式 只有一行，包括一个实数，表示所求答案。
数字保留六位小数。
数据范围
1≤N≤150,0≤X,Y≤10^5
输入样例
8
10 10
15 10
20 10
15 15
20 15
30 15
25 10
30 10
01000000
10111000
01001000
01001000
01110000
00000010
00000101
00000010
输出样例
22.071068
二、题目解析
1、梳理概念
-
牧区： 点
-
牧场： 连通块
-
边权： 两个点之间的欧几里得距离，也就是二维平面中的两点之间最短直线距离
-
牧场直径:一个牧场中的 最长最短路
-
每个节点引出的最长路径
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++)
if (dist[i][j] < INF / 2)
maxd[i] = max(maxd[i], dist[i][j]);
}
- 最长直径 =
max(每个节点引出的最长路径)res=max(maxd[A],maxd[B],maxd[C],...)
2、思考变化
使用一条边连接两个牧场，使得合成的一个新的牧场的直径最小。意思就是加入一条边后，使得新的牧场的所有点对之间 最短路 的 最大值 最小。
那么这个新的最短路该怎么计算呢？
maxd[i] + maxd[j] + get(q[i], q[j])
// maxd[i]: i 点在原牧场中的最长路径
// maxd[j]: j 点在原牧场中的最长路径
// get(q[i], q[j]): (i,j)连通后新产生的欧几里得距离
解释：假设
(i,j)是新连通的，那么原来(i,j)在各原来各个连通块中的最长路径，都可能会对 新图直径 有贡献，并且，需要加上(i,j)的欧几里得距离。
3、避坑指南
原文：所有牧场（生成的新牧场和原有牧场）中直径最大的牧场的直径尽可能小。
多么贴心的提醒！ 新的牧场直径有两种可能性：
- ①
i在原连通块A中的最长路径+j在原连通块B中的最长路径+(i,j)连通后新产生的欧几里得距离 - ②
A或B的直径，原来就不是通过i或j获得的，可能是通过k,h,g啥的获得的，就算你把i,j连接上了，可以获取到一条长的路径，但还是没有人家原来A或B连通块中旧的直径大，那新生成的连通块C的直径，还是人家旧的A或B的直径。
Code
#include <bits/stdc++.h>
using namespace std;
typedef pair<int, int> PII;
#define x first
#define y second
const int N = 160;
const int INF = 0x3f3f3f3f;
PII q[N]; // 每个点的坐标
char g[N][N]; // 邻接矩阵，记录是否中间有边
double dis[N][N]; // 每两个牧区(点)之间的距离
double maxd[N]; // maxd[i]:由i点出发，可以到达的最远的最短距离是多少
// Q:什么是最远的最短距离？
// 答：举个不太恰当的例子，比如A->B->C->D,边权都是1 ,同时存在一条A->D,边权是1。此时，有短的不取长的，所以A->D的距离是1，不是3。
// 欧几里得距离
double get(PII a, PII b) {
int x = a.x - b.x, y = a.y - b.y;
return sqrt(x * x + y * y);
}
int main() {
// 牧区:点，牧场：连通块
int n; // 点数
scanf("%d", &n);
for (int i = 0; i < n; i++) scanf("%d %d", &q[i].x, &q[i].y); // 点坐标
// 邻接矩阵,描述点与点之间的连通关系
// 这个用int还没法读入，因为它的输入是连续的，中间没有空格，讨厌啊~
// 字符数组与scanf("%s",g[i])相结合，直接写入二维数组g的每一行上，这个技巧是值得我们学习的。
for (int i = 0; i < n; i++) scanf("%s", g[i]);
// 遍历行与列，计算出每两个点之间的距离
// ① 距离只在同一连通块中存在，不同的连通块间的距离是INF
// ② 自己与自己的距离是0
// ③ 两个牧区相连，距离=sqrt((x1-x2)^2+(y1-y2)^2)
// 本质： g + q => dis
for (int i = 0; i < n; i++)
for (int j = 0; j < n; j++) {
// 1. double数组，在全局变量区，默认值是0
// 2. 当i==j时，自己到自己的距离是0，所以没动作，直接使用默认值，即d[i][i]=0,自己到自己没有距离
// 3. 当g[i][j]=='1'时，说明两者之间存在一条边，距离就是欧几里得距离计算办法
// 4. 否则就是没有路径
if (i == j)
dis[i][j] = 0;
else if (g[i][j] == '1')
dis[i][j] = get(q[i], q[j]);
else // 注意：由于dis数组是一个double类型，不能用memset(0x3f)进行初始化正无穷
dis[i][j] = INF;
}
// ① Floyd算法 k,i,j
// 原始各连通块内的多源最短路径
for (int k = 0; k < n; k++)
for (int i = 0; i < n; i++)
for (int j = 0; j < n; j++)
dis[i][j] = min(dis[i][j], dis[i][k] + dis[k][j]);
// ② (1)求出未建设两个连通块之间线路前，所有连通块的直径最大值res1
// (2)求出未建设两个连通块之间线路前，每个点的可以到达的最远最短距离,下一步做模拟连线时会用到
double res1 = 0;
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) // 求i到离i(最短路径) 最长距离
if (dis[i][j] < INF) maxd[i] = max(maxd[i], dis[i][j]);
// 所有点的最远距离PK,获取所有连通块的最大直径
res1 = max(res1, maxd[i]);
}
// ③ 模拟连线操作，看看这样连线后生成的新牧场直径会不会刷新原来的记录
double res2 = INF;
for (int i = 0; i < n; i++)
for (int j = 0; j < n; j++)
if (dis[i][j] == INF) // 如果i,j不在同一个连通块内
// 连接原来不在同一连通块中的两个点后，可以取得的最小直径
res2 = min(res2, maxd[i] + maxd[j] + get(q[i], q[j]));
// PK一下
printf("%.6lf\n", max(res1, res2));
return 0;
}