|
|
##[$AcWing$ $256$. 最大异或和](https://www.acwing.com/problem/content/258/)
|
|
|
|
|
|
### 一、题目大意
|
|
|
给定一个非负整数序列 $a$,初始长度为 $N$。
|
|
|
|
|
|
有 $M$ 个操作,有以下两种操作类型:
|
|
|
|
|
|
`A x`:添加操作,表示在序列末尾添加一个数 $x$,序列的长度 $N$ 增大 $1$。
|
|
|
`Q l r x`:询问操作,你需要找到一个位置 $p$,满足 $l≤p≤r$,使得:$a[p]⊕ a[p+1]⊕ … ⊕a[N]⊕ x$ 最大,输出这个**最大值**
|
|
|
|
|
|
**输入格式**
|
|
|
第一行包含两个整数 $N,M$,含义如问题描述所示。
|
|
|
|
|
|
第二行包含 $N$ 个 **非负整数**,表示初始的序列 $A$。
|
|
|
|
|
|
接下来 $M$ 行,每行描述一个操作,格式如题面所述。
|
|
|
|
|
|
**输出格式**
|
|
|
每个询问操作输出一个整数,表示询问的答案。
|
|
|
|
|
|
每个答案占一行。
|
|
|
|
|
|
**数据范围**
|
|
|
$N,M≤3×10^5,0≤a[i]≤10^7$。
|
|
|
|
|
|
**输入样例:**
|
|
|
```cpp {.line-numbers}
|
|
|
5 5
|
|
|
2 6 4 3 6
|
|
|
A 1
|
|
|
Q 3 5 4
|
|
|
A 4
|
|
|
Q 5 7 0
|
|
|
Q 3 6 6
|
|
|
```
|
|
|
**输出样例:**
|
|
|
```cpp {.line-numbers}
|
|
|
4
|
|
|
5
|
|
|
6
|
|
|
```
|
|
|
### 二、前导知识
|
|
|
|
|
|
#### 异或问题
|
|
|
异或问题是研究数列上异或性质的一类问题,例如 **区间最大异或**,**异或和** 相关问题等,解决这些问题通常用到下面的几个性质:
|
|
|
|
|
|
* 交换律 $a\oplus b = b \oplus a$
|
|
|
* 结合律 $(a\oplus b)\oplus c =a\oplus (b\oplus c)$
|
|
|
* 自反性 $x \oplus x =0$
|
|
|
* 或 0 不变性 $x \oplus 0 =x$
|
|
|
|
|
|
根据自反性质,区间的异或值**具有前缀和性质**,即
|
|
|
$$\bigoplus _{i=l}^{r}a_i= \left (\bigoplus _{i=1}^{l-1} a_i \right ) \bigoplus \left (\bigoplus _{i=1}^{r} a_i \right )$$
|
|
|
|
|
|
因此我们可以更方便地处理问题。
|
|
|
|
|
|
**证明**:
|
|
|
设$S(x)=a_1 \oplus a_2 \oplus ... \oplus a_x$
|
|
|
|
|
|
$$\large S(r)=a_1 \oplus a_2 \oplus ... \oplus a_r \\
|
|
|
S(l-1)=a_1 \oplus a_2 \oplus ... \oplus a_{l-1} \\
|
|
|
S(r) \oplus S(l-1) = a_l \oplus a_{l+1} ... \oplus a_r$$
|
|
|
|
|
|
|
|
|
|
|
|
#### 可持久化$Trie$
|
|
|
|
|
|
**$Q$:本题涉及到的是异或运算和,使用$Tire$树是可以理解的,但为什么一定要持久化,不持久化为什么不行?**
|
|
|
|
|
|
$A$: 之所以选择可持久化$Trie$来完成这道题,原因是:
|
|
|
* 普通最大异或值可以通过构建普通$Trie$,一路能反着走就反着走,实在走不了就正着走,来获取,这是一个贪心的思想
|
|
|
* 普通$Trie$无法解决区间$[L,R]$这样的查询问题,一查就是全套的,不知道什么进候收手
|
|
|
* 如果记录并枚举从$L$~$R$的每一个$Trie$树,就在空间和时间上过不去,这时,**持久化$Trie$树登场**
|
|
|
* $[1\sim R-1]$可以直接查找版本号为$R-1$的数据,不会取到大于等于$R-1$的数据
|
|
|
* $[L-1 \sim R-1]$的数据,其实在版本为$R-1$的树中其实都存在的,但直接取怕到$[1\sim L-2]$中去,造成错误查询, 办法就是在每个节点创建时,标识它是由哪个版本创建的,如果是$>=L-1$的,才能访问
|
|
|
|
|
|
|
|
|
**可持久化**:下面介绍 $Trie$ 是如何实现可持久化的。
|
|
|
|
|
|
既然我们现在要访问一个历史版本,那么我们直观的想法就是将每一个版本的 $Trie$ 结构体都存储下来,当需要一个新的结点时,我们完全复制一个历史版本,然后再它上面完成操作。这样的做法,正确性是显然的,但是空间开销却让人头疼。当务之急是减少存储空间,我们考虑将 $Trie$ 树上的一些 **枝条** 共用来减少空间上的浪费。
|
|
|
|
|
|
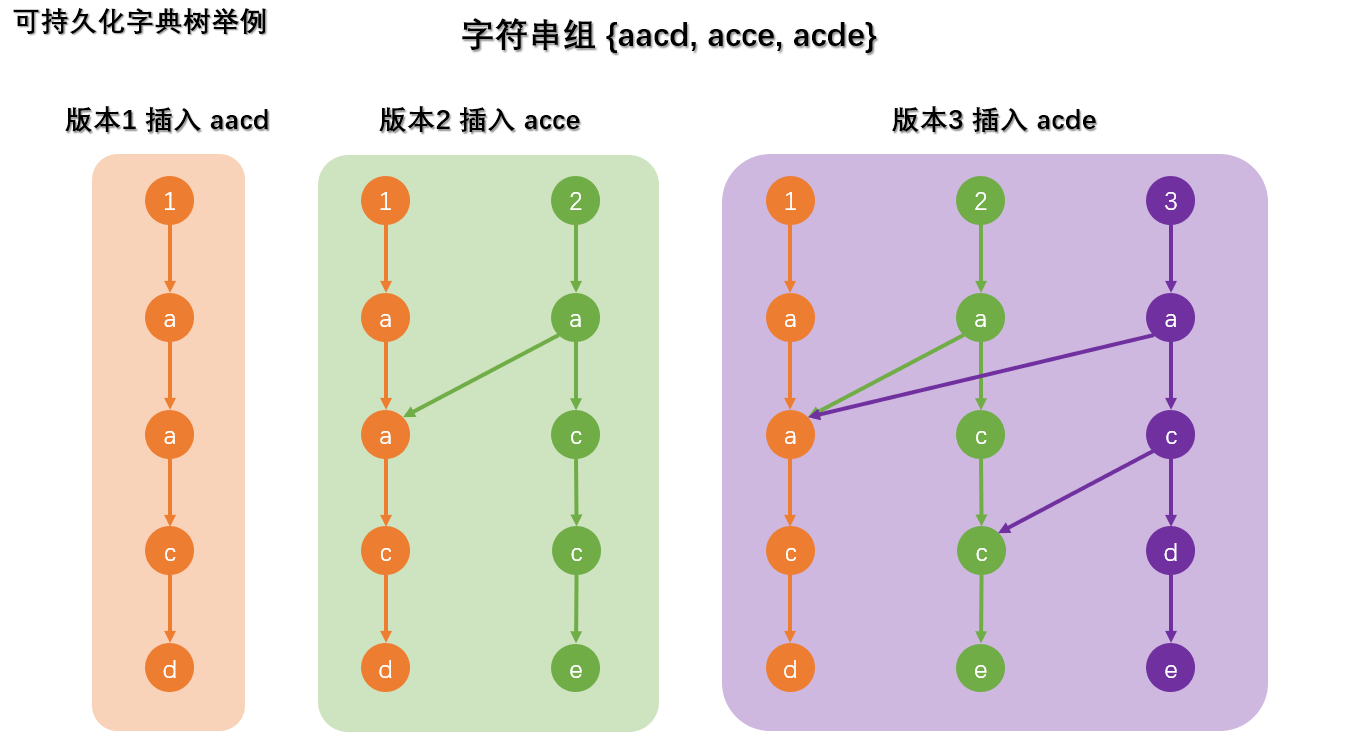
这样做:对于一个新建的版本,每插入一个点都新建一个节点,然后完全复制历史版本上同等地位点的全部儿子信息,可以看下面这张图来方便你的理解。
|
|
|
|
|
|
|
|
|
通过上图我们发现,从一个版本起点开始,遍历整棵树,一定只能获得该版本内的所有串,并且空间大大减少,是不是非常优美。
|
|
|
|
|
|
对于区间 $[l,r]$上的一些询问,我们转化为对版本$l − 1$和$r$之间插值的询问。这样就可以通过可持久化的方法来求解区间信息。
|
|
|
|
|
|
#### 图集
|
|
|
##### 1. $Trie$树中保存的是什么?
|
|
|
<center><img src='https://cdn.acwing.com/media/article/image/2021/03/12/69550_198b4f3983-%E5%8F%AF%E6%8C%81%E4%B9%85%E5%8C%96trie%E6%A0%91.png'></center>
|
|
|
|
|
|
##### 2. 可持久化$Trie$的构建步骤
|
|
|
<center><img src='https://cdn.acwing.com/media/article/image/2021/04/24/8330_69574ea4a4-trie.001.jpeg'></center>
|
|
|
|
|
|
|
|
|
### 四、本题思路
|
|
|
定义$S_i$表示前$i$个数的 **异或前缀和**,即:
|
|
|
$$S_0=0 \ S_1=a_1\ S_2=a_1⨁a_2 \ … \ S_i=a_1⨁a_2⨁a_3......⨁a_i$$
|
|
|
|
|
|
需要求解的内容变为:
|
|
|
$$a_p⨁......⨁a_n⨁x=S_{p−1}⨁S_n⨁x$$
|
|
|
|
|
|
上面的式子中可以将$S_n⨁x$看成常数,记为$C$,则相当于在区间$[L,R]$中找到一个位置$p$,使得$S_{p−1}⨁C$的值 **最大**
|
|
|
|
|
|
类似于[$AcWing$ $143$. 最大异或对](https://blog.csdn.net/weixin_42638946/article/details/115554023?spm=1001.2014.3001.5502)
|
|
|
|
|
|
将每个数据$a_i$看成一个 **二进制字符串,存入到$Trie$中**。因为$0≤a[i]≤10^7$,又$2^{23}≤a[i]≤2^{24}$,因此我们需要将每个数据对应到一个长度为$24$为的$01$二进制串上。
|
|
|
|
|
|
<font color='red'><b>先考虑简单情况</b></font>
|
|
|
假设让我们从$[1,R]$中找到一个这样的$p$的话,问题就十分类似于[$AcWing$ $143$. 最大异或对](https://blog.csdn.net/weixin_42638946/article/details/115554023?spm=1001.2014.3001.5502),**不同点** 在于本题中的$a$数组是<font color='red'><b>不断变化的</b></font>,维护一个$Trie$树,只能计算某个时刻问题。
|
|
|
|
|
|
|
|
|
因此要**记录下所有历史版本的$Trie$树**,$root[R]$中存储的就是插入$a[1\sim R]$时形成的$Trie$树。
|
|
|
|
|
|
#### 小结
|
|
|
* 利用可持久化的$Trie$树这种数据结构,可以实现从$1\sim R$区间查询。,其中$R$也就是版本号,也就是第$R$个插入的字符串。
|
|
|
|
|
|
* 如果区间左边的限制也加上,则问题就变成了让我们在区间$[L,R]$中找到一个$p$,使得$S_{p−1}⨁C$的值最大,可以这样处理:在$trie$树中的每个节点中多记录一个信息$ver$,**表示第几个版本插入的,也就是第几个数时插入的**,如果$ver[u]≥L$,则说明这棵子树在$[L,R]$这个区间中存在。
|
|
|
|
|
|
* 对于上面提到的某个$C$,数据$A$可以看成一个$24$位长度的二进制字符串,从左到右遍历这个字符串,假设当前考察的是字符$t$,则在$trie$树中我们应该走到`t ^ 1`的分支上(如果存在的话,即对于区间$[L,R]$,如果该分支对应的$ver[u]≥L$,则说明存在),这样异或值才能最大(贪心思想)
|
|
|
|
|
|
* 原序列长度为$3×10^5$,因为操作的个数最多也是$3×10^5$,因此序列的长度最大是$6×10^5$。另外还需要考虑$trie$中节点的个数:每次操作最多建立$24$个节点,再加上根节点,一共$25$个节点,每个数据最多建立$25$个节点,因此节点数为$25×6×10^5=1.5×10^7$,每个节点两个分支,因此第二维为$2$;另外还需要记录每个点的$ver$,需要的空间量是$1.5×10^7×3=4.5×10^7$个$int$,大约$4.5×10^7×4/10^6=180MB$的存储空间,题目提供$256MB$的存储空间,满足要求
|
|
|
|
|
|
### 五、实现代码
|
|
|
```cpp {.line-numbers}
|
|
|
#include <cstdio>
|
|
|
#include <cstring>
|
|
|
#include <algorithm>
|
|
|
#include <iostream>
|
|
|
#include <cmath>
|
|
|
|
|
|
using namespace std;
|
|
|
|
|
|
const int N = 6e5 + 10, M = 25 * N;
|
|
|
int s[N];
|
|
|
int tr[M][2], ver[M];
|
|
|
int root[N], idx;
|
|
|
|
|
|
void insert(int k, int p, int q) {
|
|
|
for (int i = 23; ~i; i--) {
|
|
|
int u = s[k] >> i & 1;
|
|
|
tr[q][u ^ 1] = tr[p][u ^ 1]; //复制
|
|
|
tr[q][u] = ++idx; //创建
|
|
|
ver[tr[q][u]] = k; //记录版本
|
|
|
q = tr[q][u], p = tr[p][u];
|
|
|
}
|
|
|
}
|
|
|
|
|
|
int query(int p, int l, int c) {
|
|
|
for (int i = 23; ~i ; i--) {
|
|
|
int u = c >> i & 1;
|
|
|
if (tr[p][u ^ 1] && ver[tr[p][u ^ 1]] >= l)
|
|
|
p = tr[p][u ^ 1];
|
|
|
else
|
|
|
p = tr[p][u];
|
|
|
}
|
|
|
return c ^ s[ver[p]]; // p:最终停留在的异或和最大值终点处,ver[p]这是哪个版本放进来的?,s[ver[p]]=S_{p-1}
|
|
|
}
|
|
|
|
|
|
int main() {
|
|
|
ios::sync_with_stdio(false), cin.tie(0);
|
|
|
int n, m;
|
|
|
cin >> n >> m;
|
|
|
|
|
|
// 0号版本,用于处理类似于S[1]-S[0]这样的递推边界值
|
|
|
root[0] = ++idx;
|
|
|
insert(0, 0, root[0]);
|
|
|
|
|
|
for (int i = 1; i <= n; i++) {
|
|
|
int x;
|
|
|
cin >> x;
|
|
|
root[i] = ++idx;
|
|
|
s[i] = s[i - 1] ^ x; //原数组不重要,异或前缀和数组才重要
|
|
|
insert(i, root[i - 1], root[i]);
|
|
|
}
|
|
|
|
|
|
while (m--) {
|
|
|
char op;
|
|
|
cin >> op;
|
|
|
if (op == 'A') {
|
|
|
int x;
|
|
|
cin >> x;
|
|
|
n++;
|
|
|
|
|
|
root[n] = ++idx;
|
|
|
s[n] = s[n - 1] ^ x;
|
|
|
insert(n, root[n - 1], root[n]);
|
|
|
} else {
|
|
|
int l, r, x;
|
|
|
cin >> l >> r >> x;
|
|
|
printf("%d\n", query(root[r - 1], l - 1, s[n] ^ x));
|
|
|
}
|
|
|
}
|
|
|
return 0;
|
|
|
}
|
|
|
``` |