4.3 KiB
一、题目描述
某国为了防御敌国的导弹袭击,发展出一种导弹拦截系统。
但是这种导弹拦截系统有一个缺陷:虽然 它的第一发炮弹能够到达任意的高度,但是以后每一发炮弹都不能高于前一发的高度。
某天,雷达捕捉到敌国的导弹来袭。
由于该系统还在试用阶段,所以只有一套系统,因此有可能不能拦截所有的导弹。
输入导弹依次飞来的高度(雷达给出的高度数据是不大于30000的正整数,导弹数不超过1000),计算这套系统最多能拦截多少导弹,如果要拦截所有导弹最少要配备多少套这种导弹拦截系统。
输入格式 共一行,输入导弹依次飞来的高度。
输出格式 第一行包含一个整数,表示最多能拦截的导弹数。
第二行包含一个整数,表示要拦截所有导弹最少要配备的系统数。
数据范围
雷达给出的高度数据是不大于 30000 的正整数,导弹数不超过 1000。
输入样例:
389 207 155 300 299 170 158 65
输出样例:
6
2
二、问题解析
Q1:最多拦截多少个导弹?
因为拦截系统第一下是可以任意高的,以后只能拦截和它一样高,或者比它矮的,所以,这是一个最长不上升子序列。
Q2:需要多少套拦截系统?
Dilworth 定理
- 把序列分成不升子序列的最少个数,等于序列的最长上升子序列长度
- 把序列分成不降子序列的最少个数,等于序列的最长下降子序列长度
定理法
给定正整数序列,求最长不升子序列长度,以及能覆盖整个序列的不升子序列的最少个数
问题一 套用 LIS 模型即可求解。由 Dilworth 定理,问题二等价于 另一个 LIS 长度
贪心法
对于每个数,既可以把它接到已有子序列后面,也可以建立一个新序列。要使子序列数最少,应尽量不建立新序列。此外,应让每个子序列的末尾尽可能大,这样能接的数更多。因为一个数若能接到小数后面,必然能接到大数后面,反之则不成立。根据这些想法,可总结出如下贪心流程:
从前往后扫描每个数,对于当前数
- 若现有子序列的结尾都小于它,则创建新子序列
- 否则,将它放到结尾大于等于它的最小数后面
证明 (最优解 = 贪心解)
假设存在一个最优解,他在考虑第 i 个数放入的下降子序列组中,选择了贪心解方案的后面的一个位置
具体如图所示:(绿色部分,更新了q[i+1]后为保证递增顺序,交换了q[i]和q[i+1],这一步省略了)
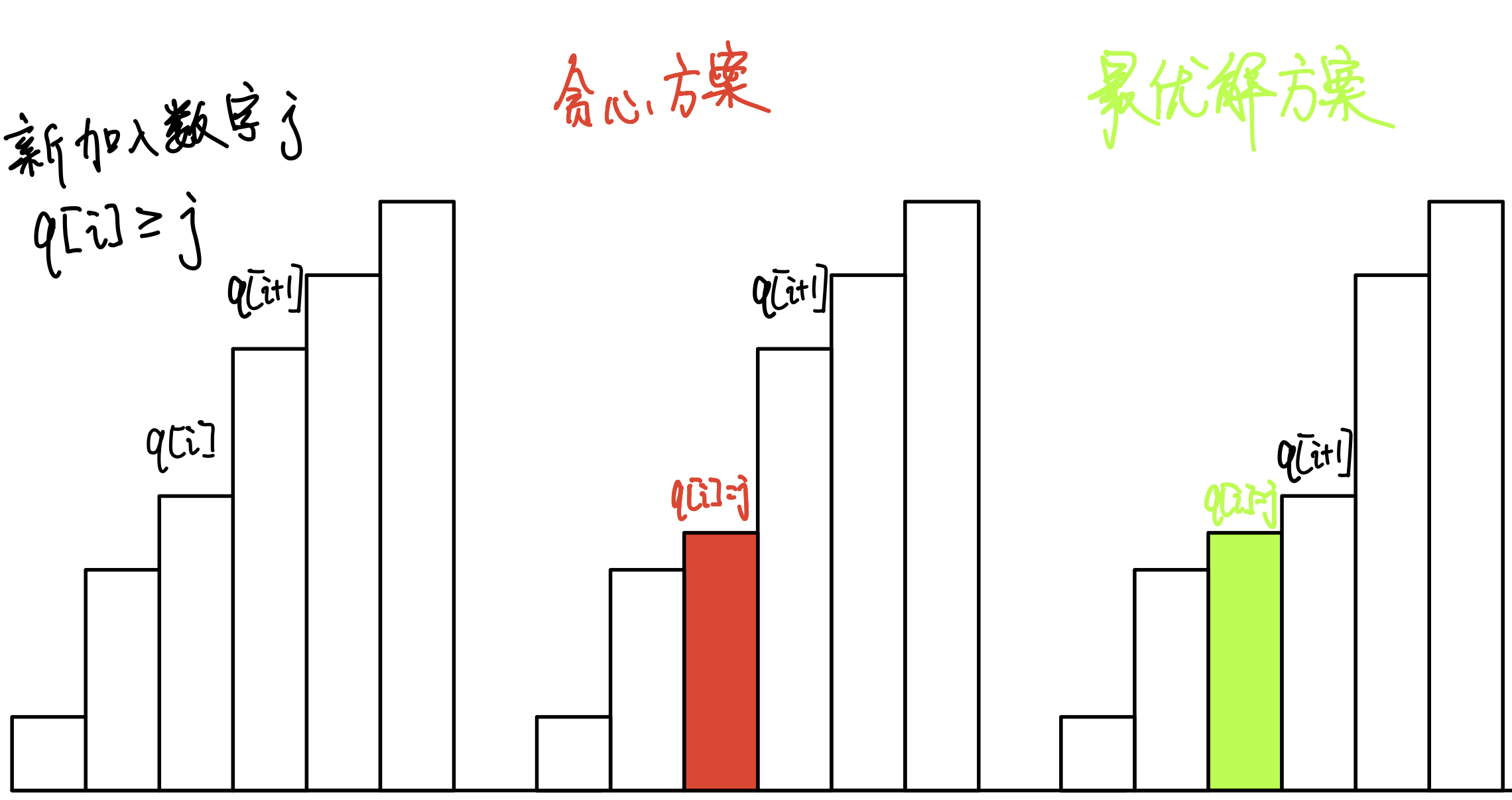
可以观察到,该最优策略使得当前局面差于贪心策略,即能接在(q[i],q[i+1])范围的子序列少了一个,即 贪心解 ≤ 最优解
同理可证,最优策略 在考虑第 i 个数放入的下降子序列组中,选择了贪心解方案的后面的第 k 个位置 也有结论 贪心解 ≤ 最优解
此外,由于贪心解 是 合法解,所以必然 贪心解 ≥ 最优解
于是有 贪心解 = 最优解
Code
朴素作法 O(N^2)
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;
int n, a[N];
int f[N], fl;
int g[N], gl;
int main() {
while (cin >> a[n]) n++;
for (int i = 0; i < n; i++) {
f[i] = 1, g[i] = 1;
for (int j = 0; j < i; j++) {
if (a[i] <= a[j])
f[i] = max(f[i], f[j] + 1); // 最长的不上升子序列长度
else
g[i] = max(g[i], g[j] + 1); // 最长单调上升子序列的长度 = 不上升子序列的覆盖数
}
fl = max(fl, f[i]), gl = max(gl, g[i]);
}
printf("%d\n%d\n", fl, gl);
return 0;
}
