python/TangDou/AcWing/LCA/352.md

AcWing 352 . 闇の連鎖

解释：暗之连锁

一、题目描述

传说中的暗之连锁被人们称为 Dark。

Dark 是人类内心的黑暗的产物，古今中外的勇者们都试图打倒它。

经过研究，你发现 Dark 呈现 无向图 的结构，图中有 N 个节点和两类边，一类边被称为 主要边，而另一类被称为 附加边。

Dark 有 N–1 条主要边，并且 Dark 的任意两个节点之间都存在一条只由主要边构成的路径。

另外，Dark 还有 M 条附加边。

你的任务是把 Dark 斩为不连通的两部分。 [提示我们：最小生成树]

① 一开始 Dark 的附加边都处于无敌状态，你只能选择一条主要边切断。

一旦你切断了一条主要边，Dark 就会进入防御模式，主要边会变为无敌的而附加边可以被切断。

② 但是你的能力只能再切断 Dark 的一条附加边。

现在你想要知道，一共有多少种方案可以击败 Dark。

注意，就算你第一步切断主要边之后就已经把 Dark 斩为两截，你也需要切断一条附加边才算击败了 Dark。

输入格式 第一行包含两个整数 N 和 M。

之后 N–1 行，每行包括两个整数 A 和 B，表示 A 和 B 之间有一条主要边。

之后 M 行以同样的格式给出附加边。

输出格式 输出一个整数表示答案。

数据范围 N≤100000,M≤200000，数据保证答案不超过2^{31}−1

输入样例：

4 1
1 2
2 3
1 4
3 4

输出样例：

3

二、题目分析

有n − 1条主要边构成一棵树，然后有m条附加边，当把其中一条附加边添加到主要边构成的树中，则会与树上x , y之间的路径上一起形成一个环。我们需要砍掉一条主要边和一条附加边，使得这棵树不再连通，成为两个独立的部分。我们需要统计有多少种不同的方案，使得这棵树不连通。

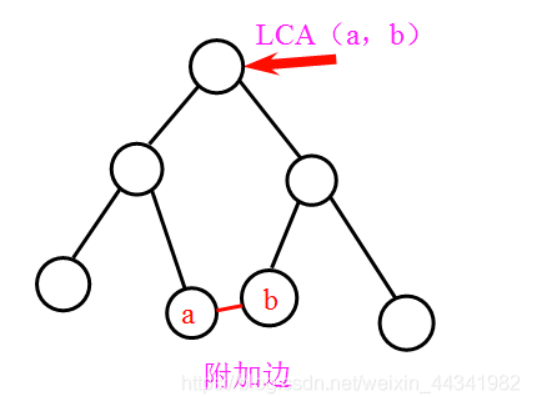
显然， 主要边 构成一棵树，而一条 附加边 必然会和其两端的LCA形成环，如图所示：

那么，对于每一条主要边，存在三种情况：

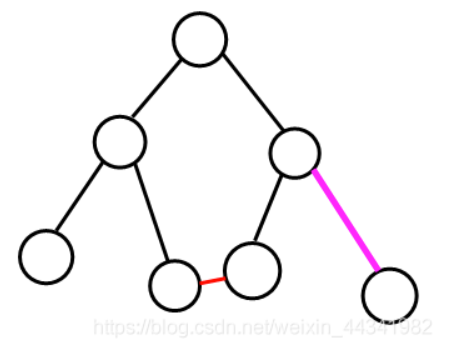
1. 没有被任何环覆盖

如下图所示：红色表示附加边，粉红色表示一条主要边，这条主要边并不在这条附加边所形成的环中

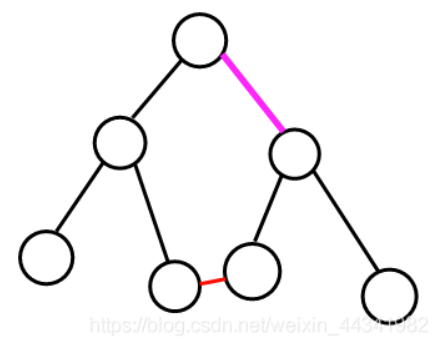
2. 只被1个环覆盖

如下图所示：红色表示附加边，粉红色表示一条主要边，这条主要边在这条附加边所形成的环中

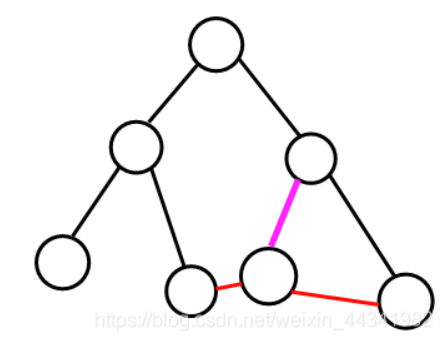
3.被2个及以上环覆盖

如下图所示：红色表示附加边，粉红色表示一条主要边，这条主要边在两条附加边所形成的两个环中

• 对于情况一，枚举的那个主要边并不在环中，很明显，我们只要把这条主要边删除，那么这个图必然是不连通的。由于题目要求必须砍掉一条主要边和砍掉一条附加边。现在砍掉了这条枚举到的主要边，那么还需要砍掉一条附加边。由于有m条附加边，因此我们有m种选择，所以此时就有m种方案。所以让答案ans累加上m即可，ans+=m

• 对于情况二，枚举的那个主要边在环中，可以发现，如果我们把这条主要边删除，要想让图不连通，必然还要再删除这条附加边，因此这是唯一的一种方案（即必然是砍掉这条枚举到的主要边和这个附加边），所以让答案ans累加上1即可，ans+=1

• 对于情况三，枚举的那个主要边在两个及以上的环中，以两个环为栗子，可以发现，如果我们把这条主要边砍掉，即使再砍掉一条附加边，这张图仍然是连通的，因此必须砍掉两条附加边，才能使得这张图变得不连通，但是题目要求只能砍掉一条主要边和砍掉一条附加边。因此，对于这种情况，不能得出方案，所以不需要累加答案。

那么我们 怎么统计每条主要边被环覆盖的次数 呢？也就是说，我们如何统计附加边(x,y)所在的那个环中每条边上的权值呢？每条边上的权值表示被附加边覆盖的次数。

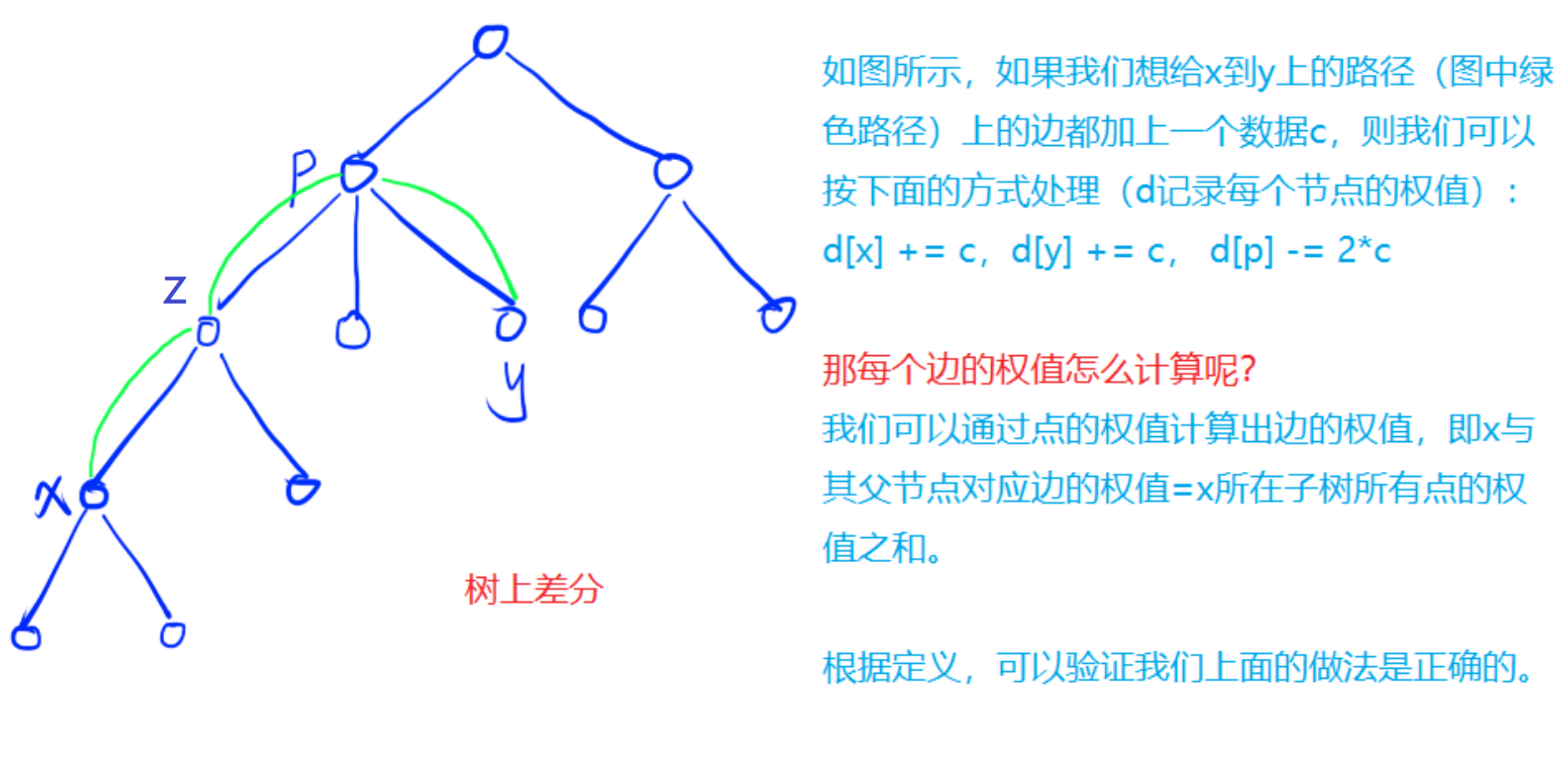
也就是我们如何让从点x出发经过它俩的lca然后到达节点y所经过的每一条边都+c呢？可以用经典算法 树上差分 来做:

d[x]、d[y] 会对它们到根节点上的每一条边都+c，d[lca]会对它们到根节点上的每一条边都-2c，那么这样最终的效果就是：让x到lca中和y到lca中的每条边都+c

树上差分

分为以下三种：

• 按点差分
• 按边差分
• 按深度差分

我们这里是按边差分，因为我们想知道每条边上的覆盖次数（可以认为是这条边的边权）。但是呢，一般按边差分不好做，我们都是将边权转换为点权，然后用按点差分来做。我们知道，每个节点最多只有1个父节点，也就是向上连的边只有1条，所以我们 把一条边的边权下放到它的子节点的点权上（注意 根节点没有点权，因为根节点上面没有边，所以没有边权下放给根节点），这样我们就转化到按点差分了。我们可以采用dfs对这棵树进行深搜，在回溯时，把子树v中的所有节点上的权值都累加到节点u上，设总和为sum，节点v的父节点是u，那么sum其实就是节点u和节点v之间的边权了，也就是覆盖次数。

以节点z所在的子树为栗子，将节点z下面的所有点权d[i]累加然后统计到节点z上，设总和为sum，那么节点p和节点z之间的边权其实就是sum。

注意： ① 对于数组f[][]，因为点数最多是1e5，由于2^{16}<1e5<2^{17} ，所以第二维的大小应该取到17，这样才能弄完全部1e$5个点。因此$fa的第二维有0\sim 16一共17个数，第二维需要设置为17。 ② 虽然说题目中有附加边，但是我们建图时，只是把主要边给建立出来，并没有把附加边建到图中去。由于最多有N个点，这是树，是无向边，因此最多有M = 2 × N条边。

算法设计

• ① 先将主要边用图建立出来
• ② 进行bfs预处理出f[][],以倍增的思路记录每个点i向上跳2^k步的节点号
• ③ 枚举每一条附加边，对于附加边所在环上的所有主要边其两端的点权都+1，预处理出差分数组d[],用来判断某条主要边被多少个环覆盖
• ④ 进行dfs，枚举每一条主要边，进行树上差分得到每条主要边上的权值。讨论每条主要边上的权值：
  • 如果c=0，则说明这条主要边并不在附加边所形成的环中，就是情况一，所以答案ans+=m
  • 如果c=1，则说明这条主要边在附加边所形成的环中，就是情况二，所以答案ans+=1
  • 如果c>1，则说明这条主要边处于多条附加边所形成的多个环中，就是情况三，不用累加答案

Code

#include <bits/stdc++.h>
using namespace std;
const int N = 100010, M = 200010;
int depth[N], f[N][25];
int n, m;
int d[N]; // 差分数组
int ans;  // 存答案
const int T = 17;
// 邻接表
int e[M], h[N], idx, ne[M];
void add(int a, int b) {
    e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
// 树上倍增
void bfs() {
    queue<int> q;
    q.push(1);
    depth[1] = 1;
    while (q.size()) {
        int u = q.front();
        q.pop();
        for (int i = h[u]; ~i; i = ne[i]) {
            int v = e[i];
            if (!depth[v]) {
                depth[v] = depth[u] + 1;
                q.push(v);
                f[v][0] = u;
                for (int k = 1; k <= T; k++) f[v][k] = f[f[v][k - 1]][k - 1];
            }
        }
    }
}
// 标准lca
int lca(int a, int b) {
    if (depth[a] < depth[b]) swap(a, b);
    for (int i = T; i >= 0; i--)
        if (depth[f[a][i]] >= depth[b]) a = f[a][i];
    if (a == b) return a;
    for (int i = T; i >= 0; i--)
        if (f[a][i] != f[b][i])
            a = f[a][i], b = f[b][i];
    return f[a][0];
}

// 前缀和
void dfs(int u, int fa) {
    for (int i = h[u]; ~i; i = ne[i]) {
        int v = e[i];
        if (v == fa) continue;
        dfs(v, u);
        d[u] += d[v];
    }
}

int main() {
    int a, b;
    scanf("%d %d", &n, &m);
    memset(h, -1, sizeof h);
    for (int i = 1; i < n; i++) { // n-1条边
        scanf("%d %d", &a, &b);
        add(a, b), add(b, a);
    }

    // lca的准备动作
    bfs();

    // 读入附加边
    for (int i = 0; i < m; i++) {
        scanf("%d %d", &a, &b);
        // 树上差分
        //  d[a]的含义：从a->fa这边条，多了一个环
        //  d[b]的含义：从b->fb这边条，多了一个环
        d[a]++, d[b]++;
        int p = lca(a, b);
        /*
        Q:lca(a,b)为什么要减2？
        A:边差分，每条边是下放到下面的那个点上，用点来表示这个边的。
        其实，每个点表示的是它向上那条边被覆盖的次数，对于lca(a,b)而言，由于dfs统计进行前缀和汇总时，
        是左子树+右子树这样的形式进行汇总的，也按同样逻辑处理就会多出2个，需要扣除掉。
        */
        d[p] -= 2;
    }

    // 差分数组求前缀和
    dfs(1, 0);
    
    // Q:为什么要从2开始？
    // A:因为1是根，1是没有边的，边是向上的，从2开始才有边
    for (int i = 2; i <= n; i++) {
        if (d[i] == 0) ans += m;
        if (d[i] == 1) ans += 1;
    }
    // 输出
    printf("%d\n", ans);
    return 0;
}

三、答疑解惑

Q:为什么认为根是1号节点，题目中也没有明确这个啊，我试了其它节点，似乎不对，这是为什么？

答：在无向图的树中，其实以谁为根来求LCA都是可以的，其它节点你的答案不对，可能是在求bfs时，忘记将第一个入队列的设置为start了，代码如下：

#include <bits/stdc++.h>
using namespace std;
const int N = 100010, M = 200010;
int depth[N], f[N][25];
int n, m;
int d[N];
int ans;
const int T = 17;

int e[M], h[N], idx, ne[M];
void add(int a, int b) {
    e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}

//将2号设置为根
int start = 2;

void bfs() {
    queue<int> q;
    q.push(start);
    depth[start] = 1;
    while (q.size()) {
        int u = q.front();
        q.pop();
        for (int i = h[u]; ~i; i = ne[i]) {
            int v = e[i];
            if (!depth[v]) {
                depth[v] = depth[u] + 1;
                q.push(v);
                f[v][0] = u;
                for (int k = 1; k <= T; k++) f[v][k] = f[f[v][k - 1]][k - 1];
            }
        }
    }
}

int lca(int a, int b) {
    if (depth[a] < depth[b]) swap(a, b);
    for (int i = T; i >= 0; i--)
        if (depth[f[a][i]] >= depth[b]) a = f[a][i];
    if (a == b) return a;
    for (int i = T; i >= 0; i--)
        if (f[a][i] != f[b][i])
            a = f[a][i], b = f[b][i];
    return f[a][0];
}

void dfs(int u, int fa) {
    for (int i = h[u]; ~i; i = ne[i]) {
        int v = e[i];
        if (v == fa) continue;
        dfs(v, u);
        d[u] += d[v];
    }
}

int main() {
    int a, b;
    scanf("%d %d", &n, &m);
    memset(h, -1, sizeof h);
    for (int i = 1; i < n; i++) {
        scanf("%d %d", &a, &b);
        add(a, b), add(b, a);
    }

    bfs();

    for (int i = 0; i < m; i++) {
        scanf("%d %d", &a, &b);

        d[a]++, d[b]++;
        int p = lca(a, b);

        d[p] -= 2;
    }

    dfs(start, 0);

    for (int i = 1; i <= n; i++) {
        if (i == start) continue;
        if (d[i] == 0) ans += m;
        if (d[i] == 1) ans += 1;
    }

    printf("%d\n", ans);
    return 0;
}