python

14 KiB

Raw Blame History Unescape Escape

This file contains ambiguous Unicode characters that may be confused with others in your current locale. If your use case is intentional and legitimate, you can safely ignore this warning. Use the Escape button to highlight these characters.

##AcWing 883. 高斯消元解线性方程组

一、题目描述

输入一个包含 n 个方程 n 个未知数的线性方程组。

方程组中的系数为实数。

求解这个方程组。

下图为一个包含 m 个方程 n 个未知数的线性方程组示例：

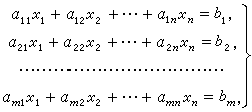
输入格式 第一行包含整数 n。

接下来 n 行，每行包含 n+1 个实数，表示一个方程的 n 个系数以及等号右侧的常数。

输出格式 如果给定线性方程组存在唯一解，则输出共 n 行，其中第 i 行输出第 i 个未知数的解，结果保留两位小数。

如果给定线性方程组存在无数解，则输出 Infinite group solutions。

如果给定线性方程组无解，则输出 No solution。

数据范围 1≤n≤100,所有输入系数以及常数均保留两位小数，绝对值均不超过 100。

输入样例：

3
1.00 2.00 -1.00 -6.00
2.00 1.00 -3.00 -9.00
-1.00 -1.00 2.00 7.00

输出样例：

1.00
-2.00
3.00

二、线性方程组知识

三、高斯消元法

求解线性方程组的办法，是高斯消元法:

通过一系列的加减消元，得到类似 kx=b 的式子，求得最后一个未知量的结果
然后逐一回代求解整个 x 向量

以下列方程为例：

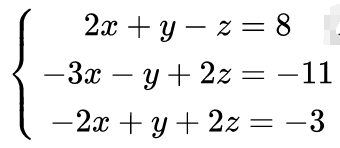
第一次加减消元，用第1式子消去后面所有的x得到：

方法：第①式左右两边除以2,然后左右两边乘以②,③式中x的系数,再分别加(减)到②,③式中,我称之为系数清零消元法

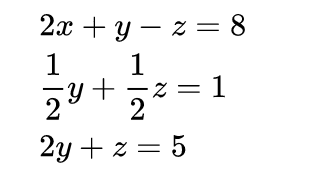
第二次加减消元，用第2个式子消去后面所有的y得到：

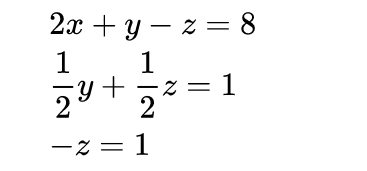
这样就完成了高斯消元的步骤1，形成了一个倒三角形的形状，接下来逐一回代即可。

用矩阵表示高斯消元

（1）消元过程：

（2）无解：当消元完毕后，发现有一行系数都为 0，但是常数项不为 0，此时无解

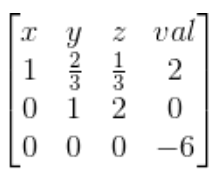
（3）多解：当消元完毕后，发现有多行系数、常数项均为 0，此时多解，有几行为全为 0，就有几个自由元，即变量的值可以任取，有无数种情况可以满足给出的方程组

此时自由元为2个

常见问题

问题一: 为什么化简为 1的操作，和清零的操作都要倒着推?

当然也可以正着推，不过要用一个变量来记录一下开头的元素的值。化简都除以这个值就行了,不过有点麻烦，倒着推时要以省一个变量~

问题二：if (abs(a[t][c]) < eps) continue;如何理解?

假设 c表示列，r表示行，此时我们进行到了 c=2 r=2

1 0 2 3
0 0 3 2
0 0 2 3

你会发现此时r行之下的c列的绝对值最大值就是0. 说明此时的第c列已经化简好了，那么不需要再进行后面的化简操作，但是此时第r行不用变，此时c加1 就接着从 第二行 第三列 开始找绝对值最大的数。如果我们的r向后移动了，那么此时我们的第2行是没有化简的，这显然是不对的。以此为例，r如果向后移动了，此时r=3,c=3但是此时我们的 第二行 第三列 是 3 并不是1这种最简的形态。

问题三：倒着推解是如何来的

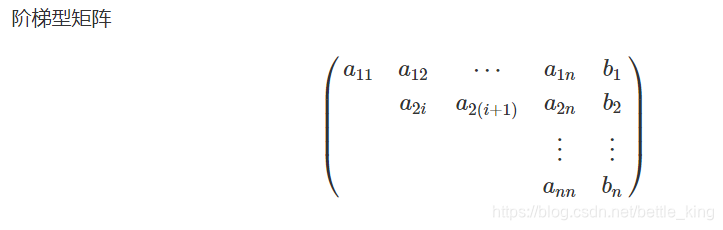
当有唯一解的时候，我们最后的化简一定是这种。解的最终形式，如下所示:

我们倒着将每一行都简成每一行只有一个1 的形式。这里模拟一下，代码就懂了。

5、手绘流程

`Code` 下标从`1`开始【推荐】

#include <bits/stdc++.h>
using namespace std;

const int N = 110;
const double eps = 1e-8; // 小数的精度值
int n;                   // n个方程
double a[N][N];          // 系数+结果矩阵

int gauss() {                                                    // 高斯消元，答案存于a[i][n]中，0 <= i < n
    int r = 1;                                                   // 先按行后按列进行计算，当前行是第1行
    for (int c = 1; c <= n; c++) {                               // 枚举每一列
        int t = r;                                               // 防破坏r,复制出t
        for (int i = r; i <= n; i++)                             // 当前行需要找它的后续行
            if (abs(a[i][c]) > abs(a[t][c])) t = i;              // t的任务是找出c列中系数最大值是哪一行
        if (abs(a[t][c]) < eps) continue;                        // 如果c列绝对值最大的系数是0, 那么处理下一列
        for (int i = c; i <= n + 1; i++) swap(a[t][i], a[r][i]); // 将绝对值最大的行与当前行交换
        for (int i = n + 1; i >= c; i--) a[r][i] /= a[r][c];     // a[r][c]:行首系数，将当前行的行首通过除法变为1,倒序
        for (int i = r + 1; i <= n; i++)                         // 用当前行r的c列，通过减法将后续行c列消成0
            for (int j = n + 1; j >= c; j--)                     // 倒序,需要保留行首，逻辑和上面是一样的，行首值是变更系数，如果正序就把系数变成1了，后面就不对了
                a[i][j] -= a[r][j] * a[i][c];                    // a[i][c]:需要变化的乘法系数，减法：对位相消
        r++;                                                     // 下一行
    }
    if (r <= n) { // 如果没有成功执行完所有行，意味着中间存在continue,也就是某一列的系数都是0
        for (int i = r; i <= n; i++)
            if (abs(a[i][n + 1]) > eps) return 0; // 系数是0，但结果不是0，无解
        return 2;                                 // 系数是0，结果也是0，x取啥都对，有无穷多组解
    }
    // 代回求每个变量值
    for (int i = n - 1; i; i--)                   // 行,倒序
        for (int j = i + 1; j <= n; j++)          // 列,倒三角,右上角应该都是0,对角线全是1
            a[i][n + 1] -= a[i][j] * a[j][n + 1]; // 系数消为0
    return 1;                                     // 有唯一解
}

int main() {
    cin >> n;
    for (int i = 1; i <= n; i++)         // n个方程
        for (int j = 1; j <= n + 1; j++) // 每行n+1个数据，因为最后一列是等号右侧值
            cin >> a[i][j];

    int t = gauss();
    if (t == 0)
        puts("No solution");
    else if (t == 2)
        puts("Infinite group solutions");
    else
        for (int i = 1; i <= n; i++) printf("%.2lf\n", a[i][n + 1]); // 保留两位小数
    return 0;
}

`Code` 下标从`0`开始【不推荐】

#include <bits/stdc++.h>
using namespace std;

const int N = 110;
const double eps = 1e-8; // 小数的精度值
int n;                   // n个方程
double a[N][N];          // 系数+结果矩阵

int gauss() {                                                // 高斯消元，答案存于a[i][n]中，0 <= i < n
    int r = 0;                                               // 先按行后按列进行计算，当前行是第1行
    for (int c = 0; c < n; c++) {                            // 枚举每一列
        int t = r;                                           // 防破坏r,复制出t
        for (int i = r; i < n; i++)                          // 当前行需要找它的后续行
            if (abs(a[i][c]) > abs(a[t][c])) t = i;          // t的任务是找出c列中系数最大值是哪一行
        if (abs(a[t][c]) < eps) continue;                    // 如果c列绝对值最大的系数是0, 那么处理下一列
        for (int i = c; i <= n; i++) swap(a[t][i], a[r][i]); // 将绝对值最大的行与当前行交换
        for (int i = n; i >= c; i--) a[r][i] /= a[r][c];     // a[r][c]:行首系数，将当前行的行首通过除法变为1,倒序
        for (int i = r + 1; i < n; i++)                      // 用当前行r的c列，通过减法将后续行c列消成0
            for (int j = n; j >= c; j--)                     // 倒序,需要保留行首，逻辑和上面是一样的，行首值是变更系数，如果正序就把系数变成1了，后面就不对了
                a[i][j] -= a[r][j] * a[i][c];                // a[i][c]:需要变化的乘法系数，减法：对位相消
        r++;                                                 // 下一行
    }
    if (r < n) { // 如果没有成功执行完所有行，意味着中间存在continue,也就是某一列的系数都是0
        for (int i = r; i < n; i++)
            if (abs(a[i][n]) > eps) return 0; // 系数是0，但结果不是0，无解
        return 2;                             // 系数是0，结果也是0，x取啥都对，有无穷多组解
    }
    // 代回求每个变量值
    for (int i = n - 2; i >= 0; i--)      // 行,倒序
        for (int j = i + 1; j < n; j++)   // 列,倒三角,右上角应该都是0,对角线全是1
            a[i][n] -= a[i][j] * a[j][n]; // 系数消为0
    return 1;                             // 有唯一解
}

int main() {
    cin >> n;
    for (int i = 0; i < n; i++)      // n个方程
        for (int j = 0; j <= n; j++) // 每行n+1个数据，因为最后一列是等号右侧值
            cin >> a[i][j];

    int t = gauss();
    if (t == 0)
        puts("No solution");
    else if (t == 2)
        puts("Infinite group solutions");
    else
        for (int i = 0; i < n; i++) printf("%.2lf\n", a[i][n]); // 保留两位小数
    return 0;
}

五. 经验教训

练习题：P3389 【模板】高斯消元法 1、一定要复制题目中输出的字符串，我就是因为No Solution -> No solution挂了第一个点 2、Luogu的模板题中，没有强制区分无解和无穷多组解。

#include <bits/stdc++.h>
using namespace std;

const int N = 110;
const double eps = 1e-8; // 小数的精度值
int n;                   // n个方程
double a[N][N];          // 系数+结果矩阵

int gauss() {                                                    // 高斯消元，答案存于a[i][n]中，0 <= i < n
    int r = 1;                                                   // 先按行后按列进行计算，当前行是第1行
    for (int c = 1; c <= n; c++) {                               // 枚举每一列
        int t = r;                                               // 防破坏r,复制出t
        for (int i = r; i <= n; i++)                             // 当前行需要找它的后续行
            if (abs(a[i][c]) > abs(a[t][c])) t = i;              // t的任务是找出c列中系数最大值是哪一行
        if (abs(a[t][c]) < eps) continue;                        // 如果c列绝对值最大的系数是0, 那么处理下一列
        for (int i = c; i <= n + 1; i++) swap(a[t][i], a[r][i]); // 将绝对值最大的行与当前行交换
        for (int i = n + 1; i >= c; i--) a[r][i] /= a[r][c];     // a[r][c]:行首系数，将当前行的行首通过除法变为1,倒序
        for (int i = r + 1; i <= n; i++)                         // 用当前行r的c列，通过减法将后续行c列消成0
            for (int j = n + 1; j >= c; j--)                     // 倒序,需要保留行首，逻辑和上面是一样的，行首值是变更系数，如果正序就把系数变成1了，后面就不对了
                a[i][j] -= a[r][j] * a[i][c];                    // a[i][c]:需要变化的乘法系数，减法：对位相消
        r++;                                                     // 下一行
    }
    if (r <= n) { // 如果没有成功执行完所有行，意味着中间存在continue,也就是某一列的系数都是0
        for (int i = r; i <= n; i++)
            if (abs(a[i][n + 1]) > eps) return 0; // 系数是0，但结果不是0，无解
        return 2;                                 // 系数是0，结果也是0，x取啥都对，有无穷多组解
    }
    // 代回求每个变量值
    for (int i = n - 1; i; i--)                   // 行,倒序
        for (int j = i + 1; j <= n; j++)          // 列,倒三角,右上角应该都是0,对角线全是1
            a[i][n + 1] -= a[i][j] * a[j][n + 1]; // 系数消为0
    return 1;                                     // 有唯一解
}

int main() {
    cin >> n;
    for (int i = 1; i <= n; i++)         // n个方程
        for (int j = 1; j <= n + 1; j++) // 每行n+1个数据，因为最后一列是等号右侧值
            cin >> a[i][j];

    int t = gauss();
    if (t == 0 || t==2)
        puts("No Solution");
    else
        for (int i = 1; i <= n; i++) printf("%.2lf\n", a[i][n + 1]); // 保留两位小数
    return 0;
}

14 KiB Raw Blame History Unescape Escape