|
|
## $P4159$ [$SCOI2009$] 迷路
|
|
|
[题目传送门](https://www.luogu.com.cn/problem/P4159)
|
|
|
|
|
|
|
|
|
> **前序知识整理**
|
|
|
> 关键词:矩阵+快速幂
|
|
|
[P1226 【模板】快速幂||取余运算](https://www.cnblogs.com/littlehb/p/16847009.html)
|
|
|
[矩阵乘法](https://www.cnblogs.com/littlehb/p/16037718.html)
|
|
|
[P3390 【模板】矩阵快速幂](https://www.cnblogs.com/littlehb/p/16039506.html)
|
|
|
[P1939 【模板】矩阵加速(数列)](https://www.luogu.com.cn/problem/P1939)
|
|
|
|
|
|
|
|
|
### 一、题目描述
|
|
|
|
|
|
**题目背景**
|
|
|
$windy$ 在 **有向图** 中迷路了。
|
|
|
|
|
|
**题目描述**
|
|
|
该有向图有 $n$ 个节点,节点从 $1$ 至 $n$ 编号,$windy$ 从节点 $1$ 出发,他必须恰好在 $t$ 时刻到达节点 $n$。
|
|
|
|
|
|
现在给出该有向图,你能告诉 $windy$ **总共有多少种不同的路径**吗?
|
|
|
|
|
|
答案对 $2009$ 取模。
|
|
|
|
|
|
注意:$windy$ 不能在某个节点逗留,且通过某有向边的时间严格为给定的时间。
|
|
|
|
|
|
**输入格式**
|
|
|
第一行包含两个整数,分别代表 $n$ 和 $t$。
|
|
|
|
|
|
第 $2$ 到第 $(n+1)$ 行,每行一个长度为 $n$ 的字符串,第 $(i + 1)$行的第 $j$ 个字符 $c_{i, j}$是一个数字字符,若为 $0$,则代表节点 $i$ 到节点 $j$ 无边,否则代表节点 $i$ 到节点 $j$ 的边的长度为 $c_{i, j}$。
|
|
|
|
|
|
**输出格式**
|
|
|
输出一行一个整数代表答案对 $2009$ 取模的结果。
|
|
|
|
|
|
### 二、题目解析
|
|
|
|
|
|
第一反应:咦?这不是图论吗??? 默默的看了眼$t$的范围($<=1e9$),**死了心**
|
|
|
<font color='red' size=4><b>
|
|
|
蒟蒻豆爸解释一下:</b></font>为什么看一眼$t$的范围就知道不是图论呢?原因就是这个$t$,一般图论就是用$floyd,bellmanFord,spfa,dijkstra$这些东东,而这些东东的时间复杂度最好也就是$O((n+m)log~m)$,一个$m$就干到了$1e9$,不$TLE$就怪了
|
|
|
|
|
|
<!-- 让表格居中显示的风格 -->
|
|
|
<style>
|
|
|
.center
|
|
|
{
|
|
|
width: auto;
|
|
|
display: table;
|
|
|
margin-left: auto;
|
|
|
margin-right: auto;
|
|
|
}
|
|
|
</style>
|
|
|
<div class="center">
|
|
|
|
|
|
| $floyd$ | $bellmanFord$ | $spfa$ | $dijkstra$ |
|
|
|
| ---- | ---- | ---- | ---- |
|
|
|
| $O(N^3)$ | $O(N\times M)$ | $O(N\times M)$ |$O((n+m)log~m)$|
|
|
|
</div>
|
|
|
|
|
|
|
|
|
$DP$!! $DP$一定可以!!!
|
|
|
<font color='red' size=4><b>
|
|
|
蒟蒻豆爸解释一下:</b></font>$DP$能做到线性复杂度就足够牛$X$了吧,就算是线性的,也一样会$TLE$,为啥呢?因为跑一遍所有边就是$1e9$~
|
|
|
|
|
|
默默的看了眼$t$的范围,又死了心
|
|
|
|
|
|
那么怎么做呢?
|
|
|
|
|
|
#### 一、边权为$1$的有向图中 两点间边权和 恰好是$k$ 的路径条数
|
|
|
首先,我们把这道题想简单一点,如果题目中的每一条边都没有边权,只用$1$或$0$来表示两个点之间是否存在边,并且用邻接矩阵来存这张图,那么我们又可以得到些什么呢?
|
|
|
|
|
|
|
|
|
**举个栗子**
|
|
|
|
|
|
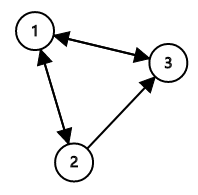
我们以下面这张图为例
|
|
|
|
|
|
|
|
|
以邻接矩阵来表示这个矩阵:
|
|
|
$\begin{bmatrix}
|
|
|
0& 1 & 1\\
|
|
|
1&0 &1 \\
|
|
|
1& 0 & 0
|
|
|
\end{bmatrix}
|
|
|
$矩阵$1$
|
|
|
|
|
|
其中,$a_{ij}$ 表示$i$到$j$之间是否有连线;
|
|
|
|
|
|
那么,我们把它 **平方** 一下,又可以得到什么呢?(友情提示:如果不清楚矩阵乘法,请[点这里](https://baike.baidu.com/item/%E7%9F%A9%E9%98%B5%E4%B9%98%E6%B3%95/5446029?fr=aladdin))
|
|
|
|
|
|
$\begin{bmatrix}
|
|
|
0& 1 & 1\\
|
|
|
1&0 &1 \\
|
|
|
1& 0 & 0
|
|
|
\end{bmatrix}
|
|
|
\times
|
|
|
\begin{bmatrix}
|
|
|
0& 1 & 1\\
|
|
|
1&0 &1 \\
|
|
|
1& 0 & 0
|
|
|
\end{bmatrix}=
|
|
|
\begin{bmatrix}
|
|
|
2& 0 & 1\\
|
|
|
1& 1 & 1 \\
|
|
|
0& 1 & 1
|
|
|
\end{bmatrix}
|
|
|
$矩阵$2$
|
|
|
|
|
|
你又发现了什么呢?
|
|
|
|
|
|
好的,如果还没发现,我们再来将矩阵$1$ **三次方**一下:
|
|
|
|
|
|
$\begin{bmatrix}
|
|
|
0& 1 & 1\\
|
|
|
1&0 &1 \\
|
|
|
1& 0 & 0
|
|
|
\end{bmatrix}
|
|
|
\times
|
|
|
\begin{bmatrix}
|
|
|
0& 1 & 1\\
|
|
|
1&0 &1 \\
|
|
|
1& 0 & 0
|
|
|
\end{bmatrix}
|
|
|
\times
|
|
|
\begin{bmatrix}
|
|
|
0& 1 & 1\\
|
|
|
1&0 &1 \\
|
|
|
1& 0 & 0
|
|
|
\end{bmatrix}=
|
|
|
\begin{bmatrix}
|
|
|
2& 0 & 1\\
|
|
|
1& 1 & 1 \\
|
|
|
0& 1 & 1
|
|
|
\end{bmatrix}
|
|
|
\times
|
|
|
\begin{bmatrix}
|
|
|
0& 1 & 1\\
|
|
|
1&0 &1 \\
|
|
|
1& 0 & 0
|
|
|
\end{bmatrix} =
|
|
|
\begin{bmatrix}
|
|
|
1& 2 & 2\\
|
|
|
2& 1 & 2 \\
|
|
|
2& 0 & 1
|
|
|
\end{bmatrix}
|
|
|
$ 矩阵$3$
|
|
|
|
|
|
什么,你还没发现吗???
|
|
|
|
|
|
那么让我来告诉你吧!!!
|
|
|
|
|
|
矩阵$1$,我们可以把$a_{ij}$ 看成通过 **一条边** ,由$i$到达$j$的情况总数
|
|
|
矩阵$2$,我们可以把$a_{ij}$ 看成通过 **两条边** ,由$i$到达$j$的情况总数
|
|
|
矩阵$3$,我们可以把$a_{ij}$ 看成通过 **三条边** ,由$i$到达$j$的情况总数
|
|
|
|
|
|
不信?我们举个栗子:
|
|
|
从点$1$到点$1$,且通过 **一条边** 的情况不存在,记为$0$;
|
|
|
从点$1$到点$1$,且通过 **两条边** 的情况共两种($1->2->1$ $and$ $1->3->1$),记为$2$;
|
|
|
从点$1$到点$1$,且通过 **三条边** 的情况仅有一种($1->2->3->1$),记为$1$;
|
|
|
|
|
|
再回头看看矩阵吧!!!是不是完全满足这个条件呢???
|
|
|
所以我们就可以得出结论啦:
|
|
|
|
|
|
**在矩阵$A^x$中,$A^x_{ij}$表示由$i$到$j$经过$x$条边的情况总数**
|
|
|
|
|
|
所以这就可以运用 **快速幂** 啦!!!
|
|
|
|
|
|
仔细算一下时间复杂度,$O(n*logn)$,稳稳滴!!!
|
|
|
|
|
|
那么,这道题就可以很快打出来啦——吗?
|
|
|
|
|
|
显然是不可以的。
|
|
|
|
|
|
可能你已经发现了,**我们所有的推论都建立在边权为$1$的情况上**,可是这道题目呢?
|
|
|
|
|
|
> 接下来有 $N$行,每行一个长度为$N$的字符串。第$i$行第$j$列为 $0$表示从节点$i$到节点$j$没有边,为$1$到$9$表示从节点$i$到节点$j$需要耗费的时间。
|
|
|
|
|
|
呀呀呀,这道题目的边权不只是$1$呀!
|
|
|
|
|
|
!(⊙ o ⊙)!
|
|
|
|
|
|
怎么办呢?
|
|
|
|
|
|
#### 二、边权不为$1$的有向图中 两点间边权和 恰好是$k$ 的路径条数
|
|
|
|
|
|
虽然我们发现不能直接使用我们的结论,但是最大边权是$9$!$N$也不超过$10$!都不算大!
|
|
|
|
|
|
那我们就可以采用一种叫做 **拆点** 的方法:把 **一个点拆成$9$个点(本质是按边权拆的)**。
|
|
|
|
|
|
并且,我们发现即使如此拆点,$N$也不会超过$100$,妥妥的可以呀!
|
|
|
|
|
|
但怎么拆点呢?
|
|
|
|
|
|
我们先来试一下拆一个边权不超过$2$的图吧!
|
|
|
|
|
|
<center><img src='https://img-blog.csdnimg.cn/99615e01cf1347c18b835be2053c87eb.png' width=40%></center>
|
|
|
|
|
|
可得矩阵
|
|
|
|
|
|
$$\large \begin{bmatrix}
|
|
|
0 & 2 \\
|
|
|
2 & 1
|
|
|
\end{bmatrix}$$
|
|
|
|
|
|
将其拆点:
|
|
|
<center><img src='https://img-blog.csdnimg.cn/d114eb837c744792bf579cbde9d99755.png' width=40%></center>
|
|
|
|
|
|
|
|
|
可得到新矩阵 :
|
|
|
$$\large \begin{bmatrix}
|
|
|
0 & 1 & 0 & 0 \\
|
|
|
0 & 0 & 1 & 0 \\
|
|
|
0 & 0 & 1 & 1 \\
|
|
|
1 & 0 & 0 & 0
|
|
|
\end{bmatrix}$$
|
|
|
|
|
|
将其平方:
|
|
|
$$\large \begin{bmatrix}
|
|
|
0 & 1 & 0 & 0 \\
|
|
|
0 & 0 & 1 & 0 \\
|
|
|
0 & 0 & 1 & 1 \\
|
|
|
1 & 0 & 0 & 0
|
|
|
\end{bmatrix}
|
|
|
\times
|
|
|
\begin{bmatrix}
|
|
|
0 & 1 & 0 & 0 \\
|
|
|
0 & 0 & 1 & 0 \\
|
|
|
0 & 0 & 1 & 1 \\
|
|
|
1 & 0 & 0 & 0
|
|
|
\end{bmatrix} =
|
|
|
\begin{bmatrix}
|
|
|
0 & 0 & 1 & 0 \\
|
|
|
0 & 0 & 1 & 1 \\
|
|
|
1 & 0 & 1 & 1 \\
|
|
|
0 & 1 & 0 & 0
|
|
|
\end{bmatrix}
|
|
|
$$
|
|
|
|
|
|
**验算一下:**
|
|
|
|
|
|
原来有点$1$到点$2$并用经过$2$边权的方案总数有一种($1->2$,边权为$2$);
|
|
|
|
|
|
现在来说,点$1$变为点$1'$,点$2$变为点$3'$,经过$2$边权的方案总数依旧是$2$($1'->2'->3'$,边权均为$1$);
|
|
|
|
|
|
那么则说明我们的拆点是正确的。
|
|
|
|
|
|
可以发现这样的话仍然是满足题意的
|
|
|
|
|
|
**这是为什么呢?为啥要这样拆点呢?**
|
|
|
|
|
|
<font color='red' size=4><b>因为可以更新答案的那条路径,一定走到了$x_i$号节点,正准备走到原来的另一个节点</b></font>
|
|
|
|
|
|
不是很好解释,自己多画几张图试试就知道了(我知道你们懒,给你们画一个)
|
|
|
|
|
|
<center><img src='https://img-blog.csdnimg.cn/a03504f45c664812ab0c2519ec846fcb.png' width=40%></center>
|
|
|
|
|
|
**拆点** 操作
|
|
|
<center><img src='https://img-blog.csdnimg.cn/60bdc2b5775a400186a538b5f6496038.png' width="40%"></center>
|
|
|
|
|
|
那么既然我们通过拆点操作将所有点之间的边权都变成了$1$,那么我们就可以用刚才得到的 **结论** 啦!!!
|
|
|
|
|
|
#### 时间复杂度
|
|
|
$O(n^3\log ~t)$
|
|
|
|
|
|
|
|
|
#### 实现代码
|
|
|
```c++
|
|
|
#include <bits/stdc++.h>
|
|
|
using namespace std;
|
|
|
|
|
|
typedef long long LL;
|
|
|
const int MOD = 2009;
|
|
|
const int N = 110;
|
|
|
|
|
|
int g[N][N], a[N][N];
|
|
|
int n, t;
|
|
|
|
|
|
//矩阵乘法
|
|
|
void mul(int c[][N], int a[][N], int b[][N]) {
|
|
|
int t[N][N] = {0};
|
|
|
int M = n * 9;
|
|
|
for (int i = 1; i <= M; i++) {
|
|
|
for (int j = 1; j <= M; j++)
|
|
|
for (int k = 1; k <= M; k++)
|
|
|
t[i][j] = (t[i][j] + (LL)(a[i][k] * b[k][j]) % MOD) % MOD;
|
|
|
}
|
|
|
memcpy(c, t, sizeof t);
|
|
|
}
|
|
|
|
|
|
int main() {
|
|
|
// n个节点,t时刻
|
|
|
scanf("%d %d", &n, &t);
|
|
|
|
|
|
for (int i = 1; i <= n; i++) { //原图有n个节点
|
|
|
|
|
|
/* 1点拆9点
|
|
|
1-> 1~9
|
|
|
2-> 10~18
|
|
|
3-> 19~17
|
|
|
...
|
|
|
|
|
|
拆开的点之间的权值是1
|
|
|
*/
|
|
|
for (int j = 1; j < 9; j++) // 1点拆9点,注意收尾处是小于号
|
|
|
g[(i - 1) * 9 + j][(i - 1) * 9 + j + 1] = 1;
|
|
|
|
|
|
//从下标1开始读入原图中i号节点与其它各节点间的边权
|
|
|
char s[11];
|
|
|
scanf("%s", s + 1);
|
|
|
|
|
|
//遍历一下输入的各点间关系图
|
|
|
for (int j = 1; j <= n; j++)
|
|
|
//如果i->j 存在边,并且边权 = s[j]
|
|
|
//比如 1->8, 边权为3; 则 从3'->64'创建一条边权为1的边
|
|
|
if (s[j] > '0') g[(i - 1) * 9 + s[j] - '0'][(j - 1) * 9 + 1] = 1;
|
|
|
}
|
|
|
|
|
|
//复制原始底图
|
|
|
memcpy(a, g, sizeof g);
|
|
|
|
|
|
//因为是复制出来,t次幂就变成了t-1次幂
|
|
|
t--;
|
|
|
|
|
|
//矩阵快速幂
|
|
|
while (t) {
|
|
|
if (t & 1) mul(g, g, a);
|
|
|
mul(a, a, a);
|
|
|
t >>= 1;
|
|
|
}
|
|
|
|
|
|
//输出结果
|
|
|
printf("%d\n", g[1][(n - 1) * 9 + 1]);
|
|
|
return 0;
|
|
|
}
|
|
|
```
|
|
|
|