|
|
## [$51nod$ $1588$ 幸运树](https://www.51nod.com/Challenge/Problem.html#problemId=1588)
|
|
|
|
|
|
#### 【知识点】树形$dp$统计树上方案数
|
|
|
|
|
|
### 一、题目描述
|
|
|
定义幸运数字只由$4$和$7$组成,比如$4$,$7$,$47$。 定义幸运数字只由$4$和$7$组成,比如$4$,$7$,$47$。
|
|
|
|
|
|
给一棵树,要我们找到三元组$(i,j,k)$,两两之间的路径中必须要有一条由幸运数字组成的边。问,存在多少组这样的三元组。
|
|
|
|
|
|
### 二、解题思路
|
|
|
幸运数字好处理,$check$一下。关键是怎么找出贡献。
|
|
|
|
|
|
统计树上方案数,**一般先固定一个点**,比如$i$,然后再找另外两个点$j$和$k$,算出$i$这个点对应的贡献。
|
|
|
|
|
|
- 设$s[i]$为以$i$为根节点的子树中,有几个点到$i$的路径中存在幸运数字
|
|
|
- 设$f[i]$为以$i$为根节点的子树外,有几个点到$i$的路径中存在幸运数字
|
|
|
|
|
|
这样,我们的 $j$ 和 $k$ 的选择就可以在$f$中选择,或者$g$中选择,或者在$f$和 $g$中选择。
|
|
|
|
|
|
即$i$的贡献为
|
|
|
$$\large s[i]*(s[i]-1)+f[i]*(f[i]-1)+s[i]*f[i]*2$$
|
|
|
|
|
|
**解释**:
|
|
|
- $s[i]*(s[i]-1)$ $j,k$都在以$i$为根节点的子树中
|
|
|
- $f[i]*(f[i]-1)$ $j,k$都在以$i$为根节点的子树外
|
|
|
- $s[i]*f[i]$ $j$在$i$为根节点的子树中,$k$在$i$为根节点的子树外
|
|
|
- $f[i]*s[i]$ $k$在$i$为根节点的子树中,$j$在$i$为根节点的子树外
|
|
|
|
|
|
然后就是处理$f$和$g$。
|
|
|
|
|
|
#### $dfs$过程中
|
|
|
|
|
|
<font color='red' size=4><b>这些式子也还是都是满满的套路啦</b></font>
|
|
|
|
|
|
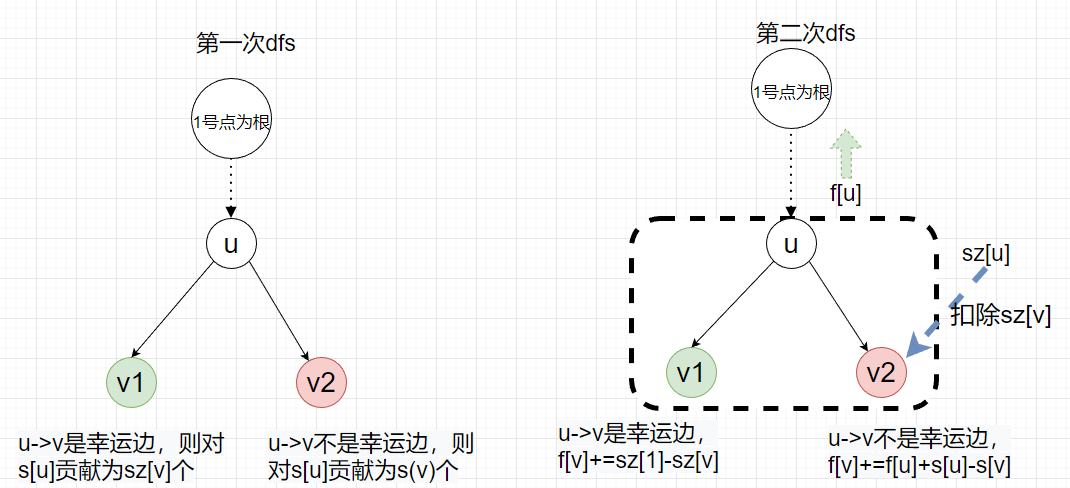
- 如果$u$和$v$的边是幸运数字,则$s[u]+=sz[v]$,否则$s[u]+=s[v]$
|
|
|
|
|
|
- 如果$v$和$u$的边是幸运数字,则$f[v]+=sz[1]-sz[v]$,否则$f[v]+=f[u]+s[u]−s[v]$
|
|
|
|
|
|
所以要先$dfs$一遍预处理$s$和$sz$,然后$dfs$一遍处理$f$,最后统计方案。
|
|
|
|
|
|
|
|
|
|
|
|
### 三、实现代码
|
|
|
|
|
|
```cpp {.line-numbers}
|
|
|
#include <bits/stdc++.h>
|
|
|
|
|
|
using namespace std;
|
|
|
|
|
|
typedef long long LL;
|
|
|
const int N = 1e6 + 10, M = N << 1;
|
|
|
|
|
|
// 链式前向星
|
|
|
int e[M], h[N], idx, w[M], ne[M];
|
|
|
void add(int a, int b, int c = 0) {
|
|
|
e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx++;
|
|
|
}
|
|
|
|
|
|
LL s[N], f[N];
|
|
|
int sz[N];
|
|
|
int st[N];
|
|
|
|
|
|
void dfs1(int u) {
|
|
|
st[u] = 1;
|
|
|
sz[u] = 1; // u节点自己加入
|
|
|
for (int i = h[u]; ~i; i = ne[i]) {
|
|
|
int v = e[i];
|
|
|
if (st[v]) continue;
|
|
|
// 先执行噢
|
|
|
dfs1(v);
|
|
|
// 统计u子树中节点数量
|
|
|
sz[u] += sz[v];
|
|
|
// 幸运边
|
|
|
if (w[i])
|
|
|
s[u] += sz[v]; // v子树中所有节点,都可以为s[u]贡献力量
|
|
|
else
|
|
|
s[u] += s[v]; // v这个点是指望不上的,它的子树中的贡献力量
|
|
|
}
|
|
|
}
|
|
|
|
|
|
void dfs2(int u) {
|
|
|
st[u] = 1;
|
|
|
for (int i = h[u]; ~i; i = ne[i]) {
|
|
|
int v = e[i];
|
|
|
if (st[v]) continue;
|
|
|
if (w[i]) // 幸运边
|
|
|
f[v] = sz[1] - sz[v]; // 容斥原理
|
|
|
else
|
|
|
f[v] = f[u] + s[u] - s[v]; // 还是容斥原理吧~
|
|
|
// 最后执行噢
|
|
|
dfs2(v);
|
|
|
}
|
|
|
}
|
|
|
|
|
|
// 幸运数字是由 4 和 7 组成的正整数
|
|
|
int check(int n) {
|
|
|
while (n) {
|
|
|
if (n % 10 != 4 && n % 10 != 7) return 0;
|
|
|
n /= 10;
|
|
|
}
|
|
|
return 1;
|
|
|
}
|
|
|
|
|
|
int main() {
|
|
|
memset(h, -1, sizeof h);
|
|
|
int n;
|
|
|
cin >> n;
|
|
|
for (int i = 1; i < n; i++) { // n-1条边
|
|
|
int a, b, c;
|
|
|
cin >> a >> b >> c;
|
|
|
c = check(c); // 如果一条边的权值是一个幸运数字,那么我们就说这条边是一条幸运边
|
|
|
add(a, b, c), add(b, a, c);
|
|
|
}
|
|
|
memset(st, 0, sizeof st);
|
|
|
dfs1(1);
|
|
|
memset(st, 0, sizeof st);
|
|
|
dfs2(1);
|
|
|
|
|
|
LL ans = 0;
|
|
|
for (int i = 1; i <= n; i++) ans += s[i] * (s[i] - 1) + f[i] * (f[i] - 1) + s[i] * f[i] * 2;
|
|
|
printf("%lld\n", ans);
|
|
|
return 0;
|
|
|
}
|
|
|
``` |