python/TangDou/AcWing/ChaFenYueShu/393.md

AcWing 393. 雇佣收银员

一、题目描述

一家超市要每天 24 小时营业，为了满足营业需求，需要雇佣一大批收银员。

已知不同时间段需要的收银员数量不同，为了能够雇佣 尽可能少 的人员，从而减少成本，这家超市的经理请你来帮忙出谋划策。

经理为你提供了一个各个时间段收银员 最小需求数量 的清单 R(0),R(1),R(2),…,R(23)。

R(0) 表示午夜 00:00 到凌晨 01:00 的最小需求数量，R(1) 表示凌晨 01:00 到凌晨 02:00 的最小需求数量，以此类推。

一共有 N 个合格的申请人申请岗位，第 i 个申请人可以从 t_i 时刻开始连续工作 8 小时。

收银员之间不存在替换，一定会完整地工作 8 小时，收银台的数量一定足够。

现在给定你收银员的需求清单，请你计算 最少需要雇佣 多少名收银员。

输入格式 第一行包含一个不超过 20 的整数，表示测试数据的组数。

对于每组测试数据，第一行包含 24 个整数，分别表示 R(0),R(1),R(2),…,R(23)。

第二行包含整数 N。

接下来 N 行，每行包含一个整数 t_i。

输出格式 每组数据输出一个结果，每个结果占一行。

如果没有满足需求的安排，输出 No Solution。

数据范围 0≤R(i)≤1000, 0≤N≤1000, 0≤t_i≤23

输入样例：

1
1 0 1 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1
5
0
23
22
1
10

输出样例：

1

二、题目分析

因为求解的是 最小值 所以需要使用 最长路 来求解，对于差分约束的题目 难点 在于 找全 题目中涉及到的不等式关系。

我们先把 基础概念 定义清楚：

• ① num[i] : i点可以来开始投入工作的人数
• ② r[i]: i点 到i+1点的最小需求数量
• ③ x_i : 从i点投入工作的人中选择的人数

解释： 1、 r(0) 表示午夜 00:00 到凌晨 01:00 的最小需求数量，r(1) 表示凌晨 01:00 到凌晨 02:00 的最小需求数量，以此类推。 2、i \in [0,23] 3、上面有用中括号括上i,有用下标标i的，原因是 ① ②是已知的，准备放入数组，而x_i是未知的，不想放入数组。

根据题目的描述,可以得到 不等式关系：

① 0 <= x_i <= num[i]

解释:每个时间点i,选中的人数，必然小于等于可选的人数。

② x_{i-7} + x_{i-6} + x_{i-5} + ... +x_i >= R_i 每一个时刻i都需要满足对应的收银员的最小数量。

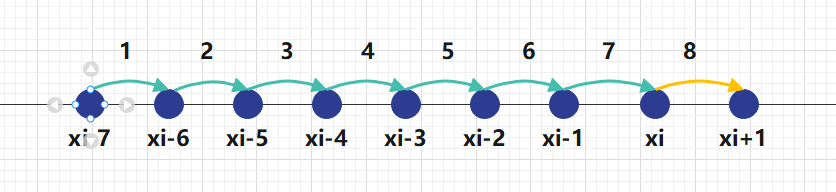
因为每个员工工作时间最长是8小时，那么如果在i这个时刻他还在工作岗位上，那么他一定是在最近8个小时内上岗的，即x_{i-7},x_{i-6},...,x_i上岗的。

对于②不是差分约束的 标准形式，但是可以发现其实加的是一整段的和所以我们考虑 前缀和 来处理，前缀和就需要考虑将0这个位置空出来。原本r[i]是表示i到i+1时段至少需要的员工数，r[0]也是有实际含义的 ,所以将所有的位置都往后移动一位，所以改为用 区间的右端点表示这段区间。

• 用r[i]表示i - 1到i时段至少需要的员工数

for (int i = 1; i <= 24; i++) scanf("%d", &r[i]);

• 用S_i表示x_1 + x_2 + ... x_i，S_0 = 0，

然后我们可以使用关于S_i的表达式来表示①②:

解释：x_i的含义是从i点中来的人中选择人数，人员是可以从0点来的，所以x_0是有效值，可我们需要用到前缀和，前缀和要求下标从1开始，所有将所有位置都往后移动一位。

对于①可以得到： 0 <= S_i - S_{i-1} <= num[i]

解释：由于照顾前缀和同学，所以x_i向后进行了错一位操作，1 <= i <= 24

对于②因为是连续工作八小时所以需要分段来看，我们以8作为分界线分为两段：

• S_i - S_{i-8} >= R_i,i >= 8
• S_i + S_{24} - S_{i+16} >= R_i,0 < i < 8 可以找一下规律，凑够八段就行

因为求解的是 最小值 所以使用 最长路 求解，也即需要将不等式整理成a >= b + c的形式，整理一下上面的不等式得到：

• S_i >= S_{i-1} + 0

• S_{i-1} >= S_i - num[i]

• S_i >= S_{i-8} + R_i，i \in [8,24]

• S_i >= S_{i+16} - S_{24} + R_i，i \in [1,7]

我们需要从超级源点s_0出发，求出到s_{24}的最长路，s_{24}就是问题的解。

注意到上面的第三个约束条件不符合差分约束的标准形式，一般的差分约束的不等式是a >= b + c，其中c是常数，这里却出现了s_{24}。

因为我们 最坏情况 下就是把n个来应聘的都招进来，所以s_{24}的最大值只能是n。这里n的范围不大，图中的点数和边数也少，直接枚举,当从小到大，找到第一个可以使得不等式组有解的S_{24}时，就是找到了答案。

解释：不等式组有解，意味着最长路无正环

注意这里对s_{24}的枚举就意味着: s_{24}在枚举的时候，它是一个常数，常数的引入，需要再加两个不等式 s(24)=c 这两个约束条件。

① \large s_{24} \geqslant c \Rightarrow s_{24} \geqslant c +s_0 \Rightarrow s_{24} \geqslant s_0 + c

 add(0, 24, c);

② \large s_{24} \leqslant c \Rightarrow s_{24} \leqslant c +s_0 \Rightarrow s_0 \geqslant s_{24} -c

add(24, 0, -c);

三、枚举

#include <bits/stdc++.h>
using namespace std;
const int N = 30, M = 100;
int n;       // n个合格的申请人申请岗位
int r[N];    // 各个时间段需要的人员数量
int num[N];  // num[i]:i点可以来工作的人数
int dist[N]; // 本题是求“最少需要雇佣”，所以是最长路
int cnt[N];  // 用于判正环（最长路）
bool st[N];  // spfa专用是否在队列中的标识

// 邻接表
int e[M], h[N], idx, w[M], ne[M];
void add(int a, int b, int c) {
    e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx++;
}
// 建图
void build(int c) {
    // 清空邻接表
    memset(h, -1, sizeof h);
    idx = 0;

    // s(i):从1点到i点，需要雇佣的人员数量
    for (int i = 1; i <= 24; i++) {
        add(i - 1, i, 0);       // s(i)   >= s(i-1) + 0
        add(i, i - 1, -num[i]); // s(i-1) >= s(i)-num[i]
    }
    // i>=8 时，s(i) >= s(i-8) + r(i)
    for (int i = 8; i <= 24; i++) add(i - 8, i, r[i]);

    // 7=>i>=1 s(i)>=s(i+16)−s(24)+r(i)
    for (int i = 1; i <= 7; i++) add(i + 16, i, -c + r[i]);

    // s24在枚举的时候，它是一个常数，常数的引入，需要再加两个不等式  s(24)=c
    add(0, 24, c);
    // s(24)>=c -> s(24) >= c +s(0)
    // -> s(24) >= s(0) + c

    add(24, 0, -c);
    // s(24)<=c -> s(24) <= c +s(0)
    // -> s(0) >= s(24) -c
}

// spfa找正环
bool spfa(int c) {
    build(c); // 建图

    // 每次初始化
    memset(st, 0, sizeof st);
    memset(cnt, 0, sizeof cnt);
    memset(dist, -0x3f, sizeof dist);
    queue<int> q;
    // 超级源点
    for (int i = 0; i <= 24; i++) {
        q.push(i);
        st[i] = true;
    }
    while (q.size()) {
        int u = q.front();
        q.pop();
        st[u] = false;
        for (int i = h[u]; ~i; i = ne[i]) {
            int v = e[i];
            if (dist[v] < dist[u] + w[i]) { // 最长路
                dist[v] = dist[u] + w[i];
                cnt[v] = cnt[u] + 1;
                // 一共24个点，发现正环了则返回false
                if (cnt[v] >= 25) return true;
                if (!st[v]) {
                    q.push(v);
                    st[v] = true;
                }
            }
        }
    }
    return false;
}

int main() {
    int T;
    scanf("%d", &T);
    while (T--) {
        // 各个时间段收银员最小需求数量的清单
        // 这里为了使用前缀和，向后进行了错一位操作
        for (int i = 1; i <= 24; i++) scanf("%d", &r[i]);
        scanf("%d", &n); // n个合格的申请人申请岗位

        memset(num, 0, sizeof num); // 多组测试数据，所以需要每次清零
        for (int i = 0; i < n; i++) {
            int t;
            scanf("%d", &t);
            // 申请人可以从num[t+1]时刻开始连续工作8小时,++代表这个时段可以干活的人数+1
            num[t + 1]++; // 这里使用了偏移量+1存储，为了照顾前缀和同学
        }
        // 枚举1~1000所有点，找到最小的
        bool success = false;
        for (int i = 1; i <= 1000; i++) // 看看当前枚举到的i是否使得SPFA有环，有环就是无解，无环就有解
            if (!spfa(i)) {
                printf("%d\n", i);
                success = true;
                break;
            }
        if (!success) puts("No Solution");
    }
    return 0;
}

四、二分

#include <bits/stdc++.h>
using namespace std;
const int N = 30, M = 100;
int n;       // n个合格的申请人申请岗位
int r[N];    // 各个时间段需要的人员数量
int num[N];  // 第i个申请人可以从num[i]时刻开始连续工作8小时
int dist[N]; // 最长距离,本题是求“最少需要雇佣”，所以是最长路
int cnt[N];  // 用于判正环（最长路）
bool st[N];  // spfa专用是否在队列中的标识
// 邻接表
int e[M], h[N], idx, w[M], ne[M];
void add(int a, int b, int c) {
    e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx++;
}
// 建图
void build(int c) {
    // 每次清空邻接表
    memset(h, -1, sizeof h);
    idx = 0;

    // s(i):从1点到i点，需要雇佣的人员数量
    for (int i = 1; i <= 24; i++) {
        add(i - 1, i, 0);       // s(i)   >= s(i-1) + 0
        add(i, i - 1, -num[i]); // s(i-1) >= s(i)-num[i]
    }
    // s(i) >= s(i-8) + r(i)
    for (int i = 8; i <= 24; i++) add(i - 8, i, r[i]);

    // s(i)>=s(i+16)−s(24)+r(i)
    for (int i = 1; i <= 7; i++) add(i + 16, i, -c + r[i]);
    // s24的引入，需要再加两个不等式  s(24)=c

    add(0, 24, c);
    // s(24)>=c -> s(24) >= c +s(0)
    // -> s(24) >= s(0) + c

    add(24, 0, -c);
    // s(24)<=c -> s(24) <= c +s(0)
    // -> s(0) >= s(24) -c
}

// spfa找正环
bool spfa(int c) {
    build(c); // 建图
    // 每次初始化
    memset(st, 0, sizeof st);
    memset(cnt, 0, sizeof cnt);
    memset(dist, -0x3f, sizeof dist);
    queue<int> q;
    // 超级源点大法好~
    for (int i = 0; i <= 24; i++) {
        q.push(i);
        st[i] = true;
    }
    while (q.size()) {
        int u = q.front();
        q.pop();
        st[u] = false;
        for (int i = h[u]; ~i; i = ne[i]) {
            int v = e[i];
            if (dist[v] < dist[u] + w[i]) { // 最长路
                dist[v] = dist[u] + w[i];
                cnt[v] = cnt[u] + 1;
                // 一共24个点，发现正环了则返回true
                if (cnt[v] >= 25) return true;
                if (!st[v]) {
                    q.push(v);
                    st[v] = true;
                }
            }
        }
    }
    return false;
}

int main() {
    int T;
    scanf("%d", &T);
    while (T--) {
        // 各个时间段收银员最小需求数量的清单
        // 这里为了使用前缀和，向后进行了错一位操作
        for (int i = 1; i <= 24; i++) scanf("%d", &r[i]);
        scanf("%d", &n); // n个合格的申请人申请岗位

        memset(num, 0, sizeof num); // 多组测试数据，所以需要每次清零
        for (int i = 0; i < n; i++) {
            int t;
            scanf("%d", &t);
            // 申请人可以从num[t+1]时刻开始连续工作8小时
            num[t + 1]++; //++代表这个时段可以干活的人数+1
        }

        // 二分总人数
        int l = 0, r = n;
        // 雇佣的人员，最少是0，最多是1000
        // 人员雇佣的越多，肯定越能满足用工要求，但成本会高
        // 所以，存在单调性，可以二分
        while (l < r) {
            int mid = (l + r) >> 1;
            if (!spfa(mid)) // 如果不等式组有解，向左逼近
                r = mid;
            else
                l = mid + 1; // 无解向右逼近
        }
        if (spfa(l)) // 如果最终计算出来的结果还是无解，那就是无解
            puts("No Solution");
        else
            printf("%d\n", l); // 输出最小值
    }
    return 0;
}