python/TangDou/AcWing/FloodFill/1106.md

AcWing 1106. 山峰和山谷

一、题目描述

FGD小朋友特别喜欢爬山，在爬山的时候他就在研究山峰和山谷。

为了能够对旅程有一个安排，他想知道山峰和山谷的数量。

给定一个地图，为FGD想要旅行的区域，地图被分为 n×n 的网格，每个格子 (i,j) 的高度 w(i,j) 是给定的。

若两个格子有公共顶点，那么它们就是相邻的格子，如与 (i,j) 相邻的格子有 (i−1,j−1),(i−1,j),(i−1,j+1),(i,j−1),(i,j+1),(i+1,j−1),(i+1,j),(i+1,j+1)。

我们定义一个格子的集合 S 为山峰（山谷）当且仅当：

1. S 的所有格子都有相同的高度。
2. S 的所有格子都连通。
3. 对于 s 属于 S，与 s 相邻的 s′ 不属于 S，都有 w_s>w_{s′}（山峰），或者 w_s<w_{s′}（山谷）。
4. 如果周围不存在相邻区域，则同时将其视为山峰和山谷。

你的任务是，对于给定的地图，求出山峰和山谷的数量，如果所有格子都有相同的高度，那么整个地图即是山峰，又是山谷。

二、题意理解

输入样例1：

5
8 8 8 7 7
7 7 8 8 7
7 7 7 7 7
7 8 8 7 8
7 8 8 8 8

输入样例2：

5
5 7 8 3 1
5 5 7 6 6
6 6 6 2 8
5 7 2 5 8
7 1 0 1 7

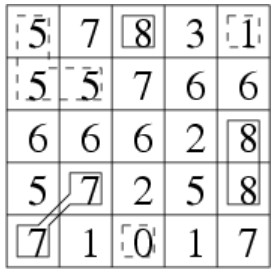
解释一下这个用例： 数字5，需要把周围和自己一样的数字连接在一起(Flood~Fill),然后看看周围是不是存在比自己 高 的，是不是存在比自己 矮 的。

• 如果周围没有比自己高的，自己就是山峰
• 如果周围没有比自己矮的，自己就是山谷

三、预备知识

• 周围八个位置遍历 八个位置一般不采用四个位置的方法，即dx[4]+dy[4]的形式，而是采用简单粗暴的九宫格遍历二层循环的办法。

• 函数的多返回值 C++的多返回值，一般采用传递\&地址符参数的方法，让函数内修改的结果返回到调用者手中。

四、bfs实现代码

#include <bits/stdc++.h>

using namespace std;
const int N = 1010, M = N * N;

typedef pair<int, int> PII;
#define x first
#define y second

int n;
int h[N][N];
PII q[M];
bool st[N][N];

/*
sx,sy:出发的位置
has_higher,has_lower:是不是周围发现了比自己高的，比自己矮的
*/
void bfs(int sx, int sy, bool &has_higher, bool &has_lower) {
    // 声明队列
    int hh = 0, tt = -1;
    // 添加出发点
    q[++tt] = {sx, sy};
    st[sx][sy] = true;

    while (hh <= tt) {
        auto t = q[hh++];
        // 利用双重循环遍历周围8连通块
        for (int i = t.x - 1; i <= t.x + 1; i++)
            for (int j = t.y - 1; j <= t.y + 1; j++) {
                if (i == 0 || i > n || j == 0 || j > n) continue; // 出地图不行
                // 下一个目标地点的高度与自己不同，需要进行标识
                if (h[i][j] != h[t.x][t.y]) {
                    if (h[i][j] > h[t.x][t.y])
                        has_higher = true;
                    else
                        has_lower = true;
                } else if (!st[i][j]) { // 与自己相同，并且没有走过
                    q[++tt] = {i, j};   // 入队列
                    st[i][j] = true;
                }
            }
    }
}

int main() {
    cin >> n;
    // 地图
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= n; j++)
            cin >> h[i][j];

    // 山峰个数，山谷个数
    int peak = 0, valley = 0;

    // Flood Fill
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= n; j++) {
            if (!st[i][j]) { // 发现新的连通块
                bool has_higher = false, has_lower = false;
                // bfs遍历连通块，标识并且找出这一块是否存在比它高的，比它矮的,使用引用返回多个值
                bfs(i, j, has_higher, has_lower);
                if (!has_higher) peak++;  // 没有比自己高的，山峰
                if (!has_lower) valley++; // 没有比自己矮的，山谷
                // 由于三种情况，山峰，山谷，即不是山峰也不是山谷，所以不能用else
            }
        }
    printf("%d %d\n", peak, valley);
    return 0;
}

五、dfs+引用参数

#include <bits/stdc++.h>
using namespace std;
const int N = 1010;

// 通过了 20/22个数据
int n;
bool st[N][N];
int h[N][N];
/*
#　不同操作系统默认栈的大小
Linux默认栈空间的大小为8MB，通过命令ulimit -s来设置
在Windows下，栈的大小是2MB

# 原因分析
每进行一次递归，都会在栈上多加一层，所以递归太深的话会出现数据溢出的错误。函数调用层次过深，每调用一次，函数的参数、
局部变量等信息就压一次栈。

n=1000 n*n=1e3*1e3=1e6
sx,sy 每个int 4byte,所以共8 byte
bool　has_higher,has_lower 各占1个byte ，所以共2byte
1e6*10=1e7 byte = 1e7/1024 kb=9,765.625  kb = 9.53mb

如果不加上 has_higher,has_lower，就是
1e6*8= 8e6/1024 kb=7,812.5kb = 7.6mb

因AcWing的评测机是GCC搭建在Linux环境中，所以栈的空间默认是8MB（我猜的，不对Y总别骂我~），也就是我们的运气好，采用全局的has_higher,
has_lower刚刚好通过这组测试数据，如果再多一点，一样是会挂掉的，这个是递归与栈的本质造成，这时只能采用bfs进行Flood Fill

#　写给AcWing
一般来说，评测时的栈空间限制等于内存限制。但系统默认的栈空间往往较小，有时会出现官方评测时正常运行，而本地测试时爆栈的情况。这时候就需要对栈空间进行更改。
现在看来AcWing的栈空间是默认的8MB，而不是CCF官方的栈空间限制等于内存限制，不知道y总是出于什么考虑。
参考链接：https://studyingfather.blog.luogu.org/noi-technical-faq


# 解决办法：
* 如果递归的层次较多，尽量避免dfs函数的参数个数，防止递归太深导致MLE出现
* 避开dfs,采用bfs即可解决，此时内存是在堆上分配的，可以使用3GB或以上

*/
void dfs(int sx, int sy, bool &has_higher, bool &has_lower) {
    st[sx][sy] = true;
    for (int x = sx - 1; x <= sx + 1; x++) {
        for (int y = sy - 1; y <= sy + 1; y++) {
            if (x <= 0 || x > n || y <= 0 || y > n) continue;
            if (h[sx][sy] != h[x][y]) { // 高度不相等
                if (h[sx][sy] < h[x][y]) has_higher = true;
                if (h[sx][sy] > h[x][y]) has_lower = true;
            } else { // 高度相等
                if (st[x][y]) continue;
                st[x][y] = true;
                dfs(x, y, has_higher, has_lower);
            }
        }
    }
}
int vally, peak;
int main() {
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= n; j++)
            cin >> h[i][j];

    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= n; j++) {
            if (!st[i][j]) {
                bool has_higher = false, has_lower = false;
                dfs(i, j, has_higher, has_lower);
                if (has_higher && has_lower) continue;
                if (has_higher) vally++;
                if (has_lower) peak++;
            }
        }
    }

    // 对于不存在山峰+山谷的一马平地，山峰山谷都输出1
    if (peak == 0 && vally == 0) peak = 1, vally = 1;
    printf("%d %d\n", peak, vally);
    return 0;
}

六、dfs+全局变量

#include <bits/stdc++.h>
using namespace std;
const int N = 1010;

int n;
bool f[N][N];
int h[N][N];
// 　将两个需要返回的参数，设置为全局变量，则可以正常通过此题。
//   将两个需要返回的参数，设置为带地址符的变量，则MLE
bool has_higher, has_lower;
//	657 ms
void dfs(int sx, int sy) {
    f[sx][sy] = true;
    for (int x = sx - 1; x <= sx + 1; x++) {
        for (int y = sy - 1; y <= sy + 1; y++) {
            if (x <= 0 || x > n || y <= 0 || y > n) continue;
            if (h[sx][sy] != h[x][y]) { // 高度不相等
                if (h[sx][sy] < h[x][y]) has_higher = true;
                if (h[sx][sy] > h[x][y]) has_lower = true;
            } else { // 高度相等
                if (f[x][y]) continue;
                dfs(x, y);
            }
        }
    }
}
int vally, peak;
int main() {
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= n; j++)
            cin >> h[i][j];

    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= n; j++) {
            if (!f[i][j]) {
                has_higher = has_lower = false;
                dfs(i, j);
                if (has_higher && has_lower) continue;
                if (has_higher) vally++;
                if (has_lower) peak++;
            }
        }
    }

    // 对于不存在山峰+山谷的一马平地，山峰山谷都输出1
    if (peak == 0 && vally == 0) peak = 1, vally = 1;
    printf("%d %d\n", peak, vally);
    return 0;
}

七、并查集解法

#include <bits/stdc++.h>
using namespace std;
const int N = 1010;
const int M = N * N;

int n;

int h[N][N];
int st[M][2]; // 第一维：并查集编号，第二维：0:附近的最小值，1：附近的最大值

// 1692 ms
// 8个方向
int dx[] = {0, 0, -1, 1, -1, 1, -1, 1}; // 上下左右
int dy[] = {1, -1, 0, 0, 1, 1, -1, -1}; // 左下，右下，左上，右上

int p[M];
int find(int x) {
    if (p[x] != x) p[x] = find(p[x]);
    return p[x];
}

// 根据坐标获取并查集的编号
void getXy(int num, int &x, int &y) {
    x = (num - 1) / n + 1;
    y = (num - 1) % n + 1;
}
// 根据并查集的编号获取坐标
int getNum(int x, int y) {
    return (x - 1) * n + y;
}

int valley, peak;
int main() {
    // 初始化并查集
    //  i为每个格子在并查集中的编号，编号策略为 (i-1)*n+j
    for (int i = 0; i < M; i++) p[i] = i; // 每个人都是自己的祖先

    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= n; j++) {
            cin >> h[i][j];
            int num = getNum(i, j);
            st[num][0] = st[num][1] = h[i][j]; // 初始化
        }

    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= n; j++)
            for (int k = 0; k < 8; k++) {
                int x = i + dx[k], y = j + dy[k];
                if (x == 0 || y == 0 || x > n || y > n) continue;
                // 编号
                int a = getNum(i, j);
                int b = getNum(x, y);
                // 族长
                int pa = find(a), pb = find(b);

                // 记录我们家族周围最小的
                if (h[i][j] > h[x][y]) st[pa][0] = min(st[pa][0], h[x][y]);
                // 记录我们家族周围最大的
                if (h[i][j] < h[x][y]) st[pa][1] = max(st[pa][1], h[x][y]);

                if (h[i][j] == h[x][y]) {
                    if (pa != pb) { // 合并并查集
                        p[pa] = pb;
                        st[pb][0] = min(st[pb][0], st[pa][0]);
                        st[pb][1] = max(st[pb][1], st[pa][1]);
                    }
                }
            }
    }

    // 没有比自己高的，山峰
    // 没有比自己矮的，山谷
    for (int i = 1; i <= n * n; i++) {
        if (p[i] == i) {
            int x, y;
            getXy(i, x, y);
            if (st[i][0] == h[x][y]) valley++;
            if (st[i][1] == h[x][y]) peak++;
        }
    }
    printf("%d %d\n", peak, valley);
    return 0;
}

八、并查集优化

因为并查集通过双重循环，从左到右，从上到下遍历，所以，可以通过双向记录周边最大最小的办法，让每个不同的区块之间互认，这样就只需要枚举 1右　2下　3右下　4左下 即可。

#include <bits/stdc++.h>
using namespace std;
const int N = 1010;
const int M = N * N;

int n;

int h[N][N];
int st[M][2]; // 第一维：并查集编号，第二维：0:附近的最小值，1：附近的最大值

// 1132 ms
int dx[] = {0, 1, 1, 1}; // 1右　2下　3右下　4左下
int dy[] = {1, 0, 1, -1};

int p[M];
int find(int x) {
    if (p[x] != x) p[x] = find(p[x]);
    return p[x];
}

// 根据坐标获取并查集的编号
void getXy(int num, int &x, int &y) {
    x = (num - 1) / n + 1;
    y = (num - 1) % n + 1;
}
// 根据并查集的编号获取坐标
int getNum(int x, int y) {
    return (x - 1) * n + y;
}

int valley, peak;
int main() {
    cin >> n;
    // 初始化并查集
    //  i为每个格子在并查集中的编号，编号策略为 (i-1)*n+j
    for (int i = 0; i < M; i++) p[i] = i; // 每个人都是自己的祖先

    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= n; j++) {
            cin >> h[i][j];
            int num = getNum(i, j);
            st[num][0] = st[num][1] = h[i][j]; // 初始化
        }

    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= n; j++)
            for (int k = 0; k < 4; k++) {
                int x = i + dx[k], y = j + dy[k];
                if (x == 0 || y == 0 || x > n || y > n) continue;
                // 编号
                int a = getNum(i, j), b = getNum(x, y);
                // 族长
                int pa = find(a), pb = find(b);

                // 记录我们家族周围最小的
                if (h[i][j] > h[x][y]) {
                    st[pa][0] = min(st[pa][0], h[x][y]);
                    st[pb][1] = max(st[pb][1], h[i][j]);
                }
                // 记录我们家族周围最大的
                if (h[i][j] < h[x][y]) {
                    st[pa][1] = max(st[pa][1], h[x][y]);
                    st[pb][0] = min(st[pb][0], h[i][j]);
                }

                if (h[i][j] == h[x][y]) {
                    if (pa != pb) { // 合并并查集
                        p[pa] = pb;
                        st[pb][0] = min(st[pb][0], st[pa][0]);
                        st[pb][1] = max(st[pb][1], st[pa][1]);
                    }
                }
            }
    }

    // 没有比自己高的，山峰
    // 没有比自己矮的，山谷
    for (int i = 1; i <= n * n; i++) {
        if (p[i] == i) {
            int x, y;
            getXy(i, x, y);
            if (st[i][0] == h[x][y]) valley++;
            if (st[i][1] == h[x][y]) peak++;
        }
    }
    printf("%d %d\n", peak, valley);
    return 0;
}