python/TangDou/Topic/【最短路径】Dijkstra算法专题.md

## $Dijkstra$算法专题

### 一、解决的问题
计算从 **源** 到所有其他各顶点的最短路径长度。这里的长度是指路上各边权之和。这个问题通常称为单源最短路径问题。

### 二、算法原理
![](https://dsideal.obs.cn-north-1.myhuaweicloud.com/HuangHai/BlogImages/202312180745532.png)

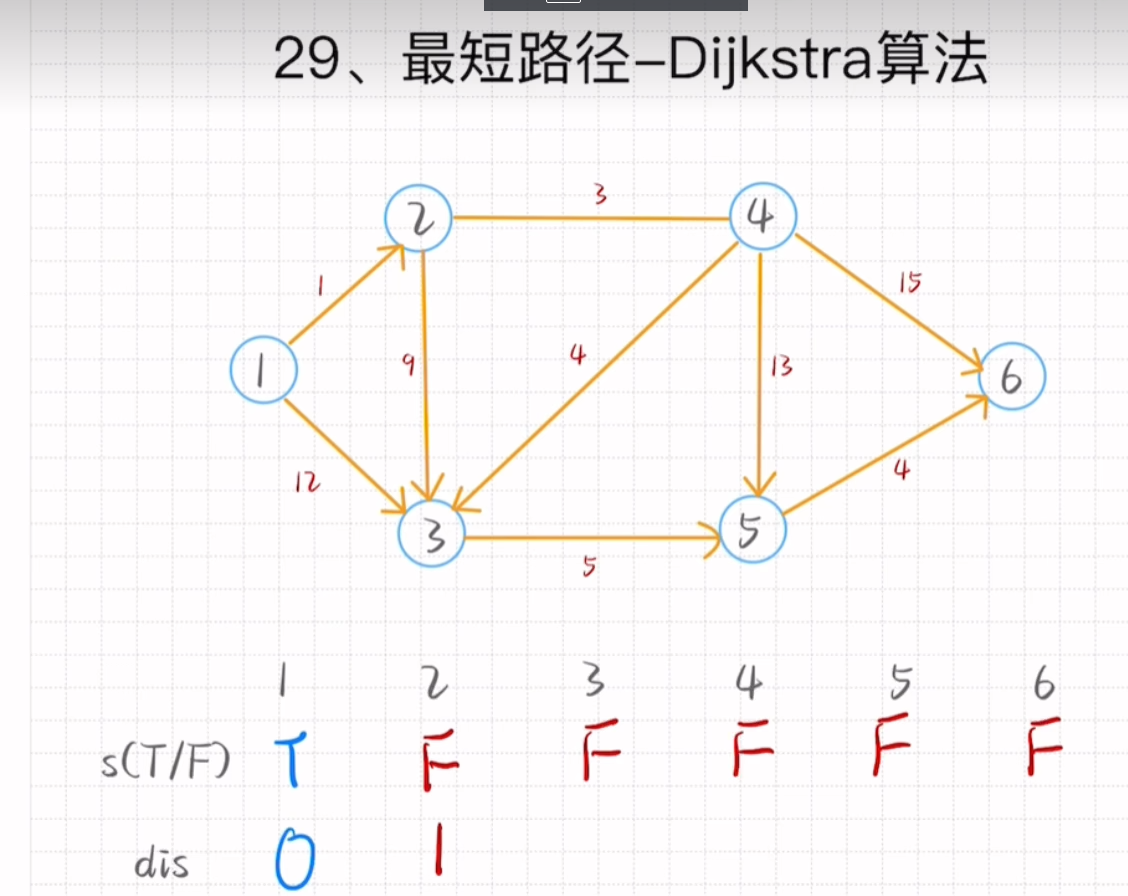
> **视频讲解** : **[【5分钟搞定$Dijkstra$算法】](https://www.bilibili.com/video/BV1ha4y1T7om)**

### 三、题单
#### 【模板题】[$AcWing$ $850$. $Dijkstra$求最短路 $II$](https://www.acwing.com/problem/content/description/852/) 

输入样例
```cpp {.line-numbers}
3 3
1 2 2
2 3 1
1 3 4
```
输出样例
```cpp {.line-numbers}
3
```
**$Code$**
```cpp {.line-numbers}
#include <bits/stdc++.h>

using namespace std;
typedef pair<int, int> PII;
const int INF = 0x3f3f3f3f;
const int N = 150010, M = N << 1;

int st[N];
int dis[N]; // 距离数组

// 邻接表
int e[M], h[N], idx, w[M], ne[M];
void add(int a, int b, int c) {
    e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx++;
}

int n, m;
int dijkstra() {
    memset(dis, 0x3f, sizeof dis);
    dis[1] = 0;
    priority_queue<PII, vector<PII>, greater<PII>> q; // 小顶堆
    q.push({0, 1});

    while (q.size()) {
        PII t = q.top();
        q.pop();
        int u = t.second;
        if (!st[u]) {
            st[u] = 1;
            for (int i = h[u]; ~i; i = ne[i]) {
                int v = e[i];
                if (dis[v] > dis[u] + w[i]) {
                    dis[v] = dis[u] + w[i];
                    q.push({dis[v], v});
                }
            }
        }
    }
    if (dis[n] == INF) return -1;
    return dis[n];
}
int main() {
    cin >> n >> m;
    memset(h, -1, sizeof h);
    while (m--) {
        int a, b, c;
        cin >> a >> b >> c;
        add(a, b, c);
    }
    printf("%d\n", dijkstra());
    return 0;
}
```

### [$AcWing$ $1129$. 热浪](https://www.acwing.com/problem/content/description/1131/)
与模板相比，只是起点和终点是输入的，其它无区别。

**$Code$**
```cpp {.line-numbers}
#include <bits/stdc++.h>
using namespace std;
const int N = 2510;
const int M = 6200 * 2 + 10;

typedef pair<int, int> PII;

int h[N], w[M], e[M], ne[M], idx;
bool st[N];
int dis[N];

void add(int a, int b, int c) {
    e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx++;
}

int n, m, S, T;

int dijkstra() {
    memset(dis, 0x3f, sizeof dis);
    dis[S] = 0;

    priority_queue<PII, vector<PII>, greater<PII>> q;
    q.push({0, S});
    while (q.size()) {
        PII t = q.top();
        q.pop();
        int u = t.second;
        if (st[u]) continue;
        st[u] = true;
        for (int i = h[u]; ~i; i = ne[i]) {
            int v = e[i];
            if (dis[v] > dis[u] + w[i]) {
                dis[v] = dis[u] + w[i];
                q.push({dis[v], v});
            }
        }
    }
    return dis[T];
}

int main() {
    cin >> n >> m >> S >> T;
    memset(h, -1, sizeof h);

    while (m--) {
        int a, b, c;
        cin >> a >> b >> c;
        add(a, b, c), add(b, a, c);
    }
    printf("%d\n", dijkstra());
    return 0;
}
```

#### [$AcWing$ $1128$. 信使](https://www.acwing.com/problem/content/1130/)
**总结**：从$1$号哨所出发，计算出到每个哨所的最短路径，所以最短路径中最长的，表示需要的最少时间，是一个最短路径模板+思维问题。

**$Code$**

```cpp {.line-numbers}
#include <bits/stdc++.h>
using namespace std;
typedef pair<int, int> PII;
const int INF = 0x3f3f3f3f;
const int N = 110;
const int M = 2 * 210; // 无向图，需要开二倍的数组长度！

int n, m;
int h[N], e[M], w[M], ne[M], idx;
void add(int a, int b, int c) {
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++;
}
int dis[N];
bool st[N];

int dijkstra() {
    memset(dis, 0x3f, sizeof dis);
    dis[1] = 0;

    priority_queue<PII, vector<PII>, greater<int>> q;
    q.push({0, 1});

    while (q.size()) {
        PII t = q.top();
        q.pop();
        int u = t.second;
        if (st[u]) continue;
        st[u] = true;

        for (int i = h[u]; ~i; i = ne[i]) {
            int v = e[i];
            if (dis[v] > dis[u] + w[i]) {
                dis[v] = dis[u] + w[i];
                q.push({dis[v], v});
            }
        }
    }
    int mx = 0;
    for (int i = 1; i <= n; i++) {
        if (dis[i] == INF) return -1;
        mx = max(mx, dis[i]);
    }
    return mx;
}
int main() {
    memset(h, -1, sizeof h);
    cin >> n >> m;
    while (m--) {
        int a, b, c;
        cin >> a >> b >> c;
        add(a, b, c), add(b, a, c);
    }
    printf("%d\n", dijkstra());
    return 0;
}

```