You can not select more than 25 topics
Topics must start with a letter or number, can include dashes ('-') and can be up to 35 characters long.
5.7 KiB
5.7 KiB
Tarjan——强连通分量
首先了解几个概念:强连通,强连通图,强连通分量
-
强连通:在一个有向图
G中,两个点a,b,a可以走到b,b可以走到a,我们就说(a,b)强连通 -
强连通图:在一个有向图
G中,任意两个点都是强连通 -
强连通分量:在一个有向图
G中,有一个子图,它任意两个点都是强连通,我们就说这个子图为强连通分量,特别的,一个点也是一个强连通分量
如图所示:

显然可得:1,2,3,5 构成了一个强连通分量(一个点也是)
首先引进一个概念:
-
时间戳,用数组
dfn表示,也就是搜索这个图的顺序,每个节点的时间戳不同。 -
low[x],以x为根的子树中,每个节点中连接的点的时间戳的最小值low的初值:low[x]=dfn[x]可能有点难懂,但这个非常重要,是核心思想,等一下的模拟过程会详细讲述 -
如何储存强连通分量呢,可以用 栈
算法步骤
- 每次遍历到一个新节点,就把它放进栈,如果这个点有出度,就继续往下找,直到不能再找
- 每一次回来都要更新
low值,当然是取小的那个,如果发现low[x]=dfn[x]那么它的子节点中肯定有一个连上来,既然可以过去又可以回来,很明显是一个强连通分量。那么这个x就是这个强连通分量的根节点,那么栈中间,比这个x晚进来的点就是x的子节点,那么这些点全部出栈,就组成了一个强连通分量
到这来就完了,但是好像还是 没有理解透彻(反正我是这样)
那么就模拟一下,还是这张图5->4
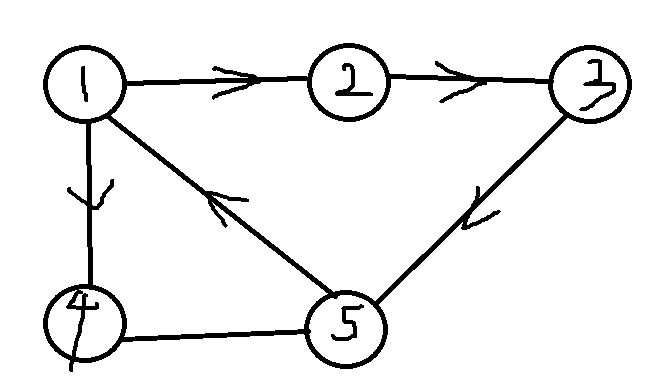
-
low[1]=dfn[1]=1,1入栈 -
low[2]=dfn[2]=2,2入栈 -
low[3]=dfn[3]=3,3入栈 -
low[5]=dfn[5]=4,5入栈
然后发现5连接着1,已经1寻找过的了,那么就看看,PK下谁才是真正的祖先
low[1]=1,low[5]=4,好吧,5输了,所以1是5的根节点,
\large low[5]=min(low[5],low[1])=1继续发现还有4,low[4]=dfn[4]=5, 4入栈
但是4已经没有了出度,往回退
发现low[4]=dfn[4]那么4就是一个强连通分量的根节点(其实也就它一个),4退栈
继续往回退:low[5]=min(low[5],low[4])=1;
继续:一直到1,
\large low[3]=min(low[3],low[5])=1 \\
low[2]=min(low[2],low[3])=1 \\
low[1]=min(low[1],low[2])=1$$
发现此时$low[1]=dfn[1]$,所以$1$也是 **一个强连通分量的根**,此时发现栈里还有$1,2,3,5$,所以这个强连通分量为$1,2,3,5$
$1$还有一个出度:$4$
寻找$4$,$low[4]=dfn[4]=5$,发现没有出度
$low[4]=dfn[4]$,所以$4$是一个强连通分量的根节点(还是只有他一个),退栈
往回退,$low[1]=min(low[1],dfn[4])=1$;
这样就完了吗?
万一还有图没有遍历到呢
所以要加一个语句:
```c++
for (int i = 1; i <= n; i++)
if (!dfn[i]) tarjan(i);
```
#### 练习题
[P2863 [USACO06JAN]The Cow Prom S](https://www.luogu.com.cn/problem/P2863)
**题目描述**
有一个 $n$ 个点,$m$ 条边的有向图,请求出这个图点数大于 $1$ 的强联通分量个数。
**输入格式**
第一行为两个整数 $n$ 和 $m$。
第二行至 $m+1$ 行,每一行有两个整数 $a$ 和 $b$,表示有一条从 $a$ 到 $b$ 的有向边。
**输出格式**
仅一行,表示点数大于 $1$ 的强联通分量个数。
```c++
#include <bits/stdc++.h>
using namespace std;
const int N = 50002, M = N << 1;
int n, m, ans;
int stk[N], top; // tarjan算法需要用到的堆栈
bool in_stk[N]; // 是否在栈内
int dfn[N]; // dfs遍历到u的时间
int low[N]; // 从u开始走所能遍历到的最小时间戳
int ts; // 时间戳,dfs序的标识,记录谁先谁后
int id[N], scc_cnt; // 强连通分量块的最新索引号
int sz[N]; // sz[i]表示编号为i的强连通分量中原来点的个数
//链式前向星
int e[M], h[N], idx, w[M], ne[M];
void add(int a, int b, int c = 0) {
e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx++;
}
// tarjan算法求强连通分量
void tarjan(int u) {
dfn[u] = low[u] = ++ts;
stk[++top] = u;
in_stk[u] = 1;
for (int i = h[u]; ~i; i = ne[i]) {
int j = e[i];
if (!dfn[j]) {
tarjan(j);
low[u] = min(low[u], low[j]);
} else if (in_stk[j])
low[u] = min(low[u], dfn[j]);
}
if (dfn[u] == low[u]) {
++scc_cnt; // 强连通分量的序号
int x; // 临时变量x,用于枚举栈中当前强连通分量中每个节点
do {
x = stk[top--]; //弹出节点
in_stk[x] = false; //标识不在栈中了
id[x] = scc_cnt; //记录每个节点在哪个强连通分量中
sz[scc_cnt]++; //这个强连通分量中节点的个数+1
} while (x != u);
}
}
int main() {
memset(h, -1, sizeof h);
scanf("%d %d", &n, &m);
for (int i = 1; i <= m; i++) {
int a, b;
scanf("%d %d", &a, &b);
add(a, b);
}
for (int i = 1; i <= n; i++)
if (!dfn[i]) tarjan(i);
//枚举结果数组,统计题目要求的 点数大于 1 的强联通分量个数
for (int i = 1; i <= scc_cnt; i++)
if (sz[i] > 1) ans++;
printf("%d\n", ans);
return 0;
}
```