6.6 KiB
AcWing 275. 传纸条
一、题目描述
小渊和小轩是好朋友也是同班同学,他们在一起总有谈不完的话题。
一次素质拓展活动中,班上同学安排坐成一个 m 行 n 列的矩阵,而小渊和小轩被安排在矩阵对角线的两端,因此,他们就无法直接交谈了。
幸运的是,他们可以通过传纸条来进行交流。
纸条要经由许多同学传到对方手里,小渊坐在矩阵的左上角,坐标 (1,1),小轩坐在矩阵的右下角,坐标 (m,n)。
从小渊传到小轩的纸条只可以 向下 或者 向右 传递,从小轩传给小渊的纸条只可以 向上 或者 向左 传递。
在活动进行中,小渊希望给小轩传递一张纸条,同时希望小轩给他回复。
班里每个同学都可以帮他们传递,但只会帮他们一次,也就是说如果此人在小渊递给小轩纸条的时候帮忙,那么在小轩递给小渊的时候就不会再帮忙,反之亦然。
还有一件事情需要注意,全班每个同学愿意帮忙的好感度有高有低(注意:小渊和小轩的好心程度没有定义,输入时用 0 表示),可以用一个 0∼100 的自然数来表示,数越大表示越好心。
小渊和小轩希望尽可能找好心程度高的同学来帮忙传纸条,即找到来回两条传递路径,使得这两条路径上同学的好心程度之和最大。
现在,请你帮助小渊和小轩找到这样的两条路径。
输入格式
第一行有 2 个用空格隔开的整数 m 和 n,表示学生矩阵有 m 行 n 列。
接下来的 m 行是一个 m×n 的矩阵,矩阵中第 i 行 j 列的整数表示坐在第 i 行 j 列的学生的好心程度,每行的 n 个整数之间用空格隔开。
输出格式 输出一个整数,表示来回两条路上参与传递纸条的学生的好心程度之和的最大值。
数据范围
1≤n,m≤50
输入样例:
3 3
0 3 9
2 8 5
5 7 0
输出样例:
34
二、题目解析
这题明显不是一个裸题,我们需要一层一层的拆解分析
首先想到的是能不能往 方格取数 模型上靠
对于一个从 (n,m) 出发到 (1,1) 的路线,且只能向上或向左走,考虑将其 方向调转,则必定对应一条从 (1,1) 出发到 (n,m) 的路线,且只能向下或向右走
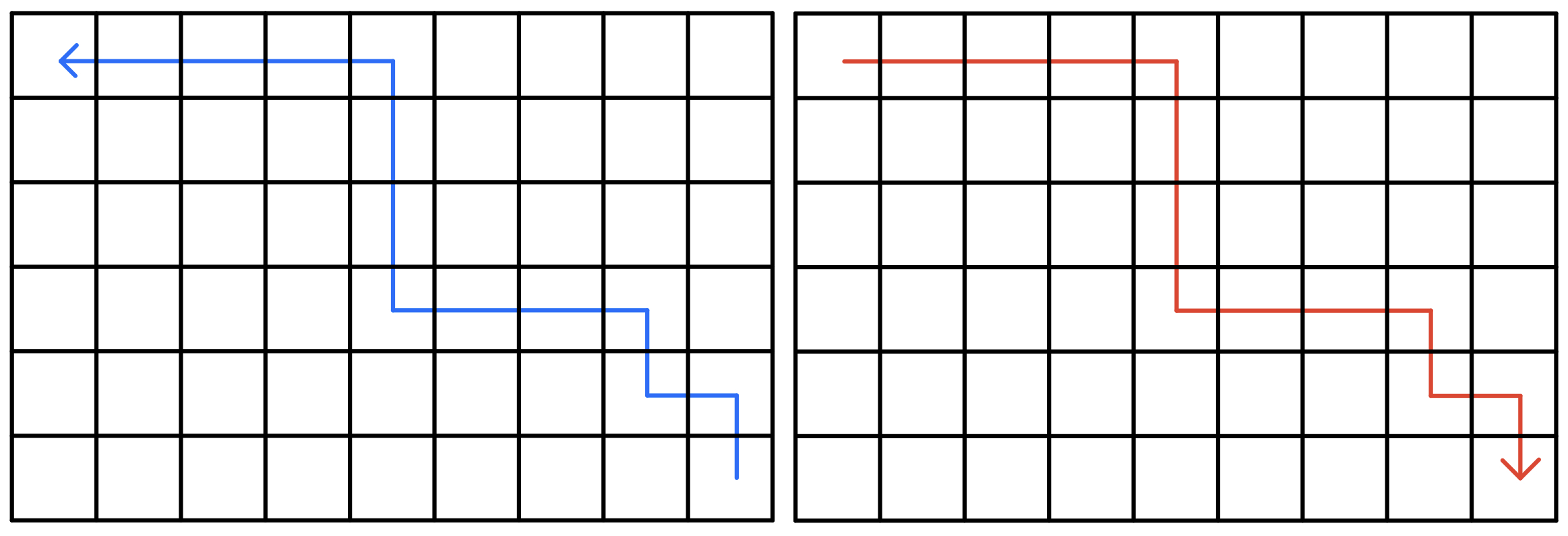
这两种走法的方案都是一一对应的(即任意一条路线都可以找到其对应的反向路线),因此该方案 映射合法
于是该问题就变成了寻找一条从 (1,1) 出发到达 (n,m),每次只能 向下 或 向右 走,先后出发两次,且两次路线 不能经过重复格子 的 最大价值方案
这样就很靠近 方格取数 模型了
关于如何解决不能经过重复格子的问题
我们先给定一个结论: 方格取数 dp模型的最优方案可以是不经过重复格子的
证明:
情况一:最优解的两条路线是相互交叉经过的
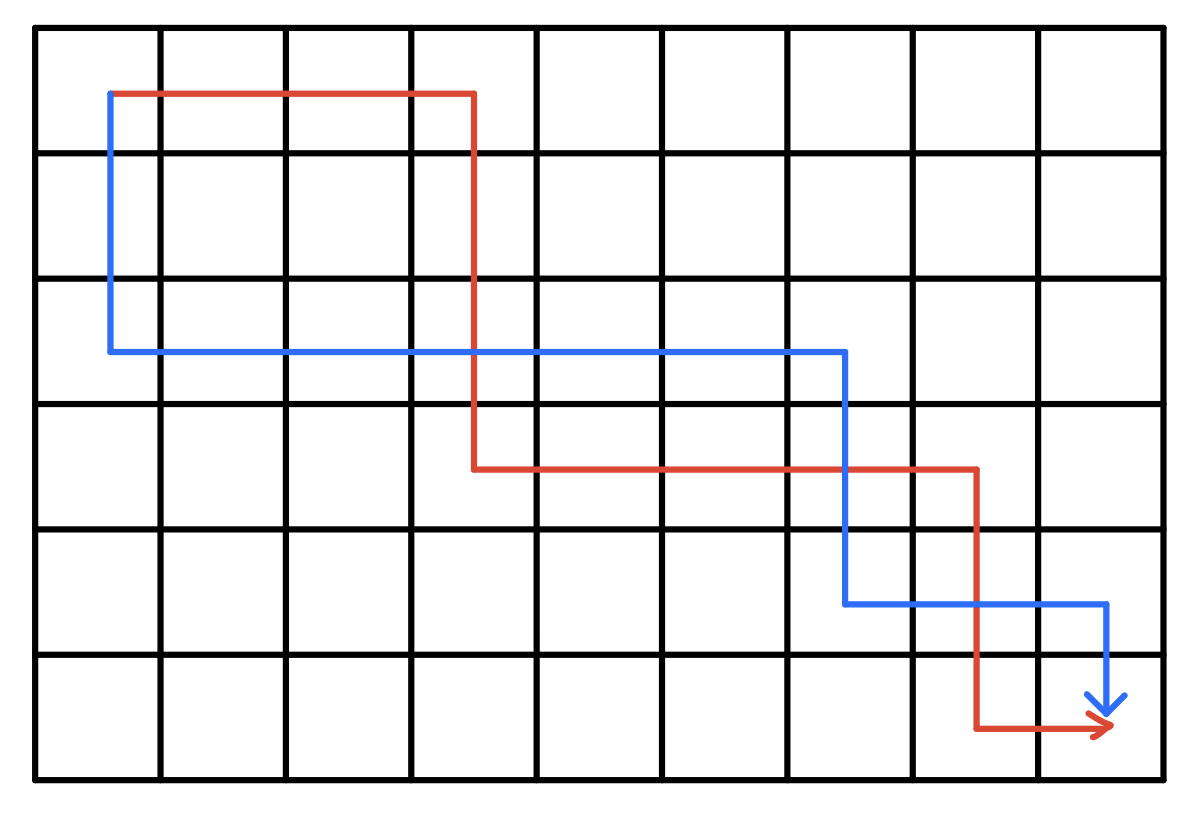
则我们可以对交叉出来的部分进行路线交换,如下图的操作
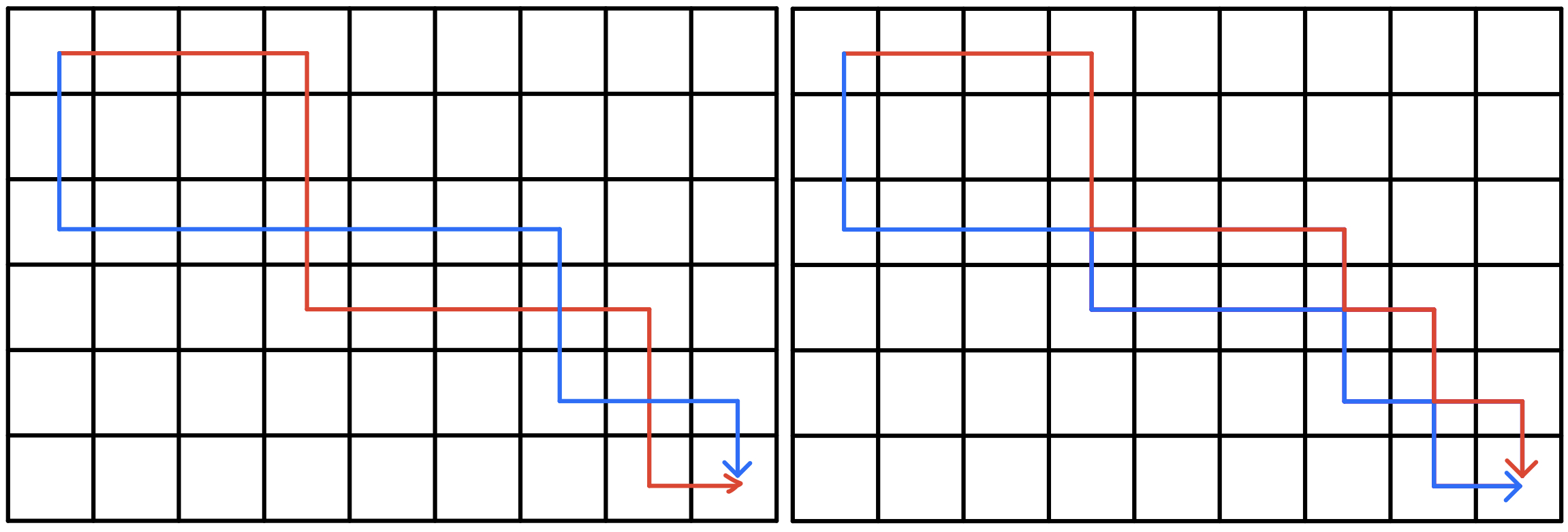
于是,我们可以发现,所有的交叉路线都会映射成一种一条路线 只在下方走,一条路线 只在上方走 的 不交叉路线
因此我们只需集中解决情况二即可
情况二:最优解的两条路线不交叉,但在某些点有重合
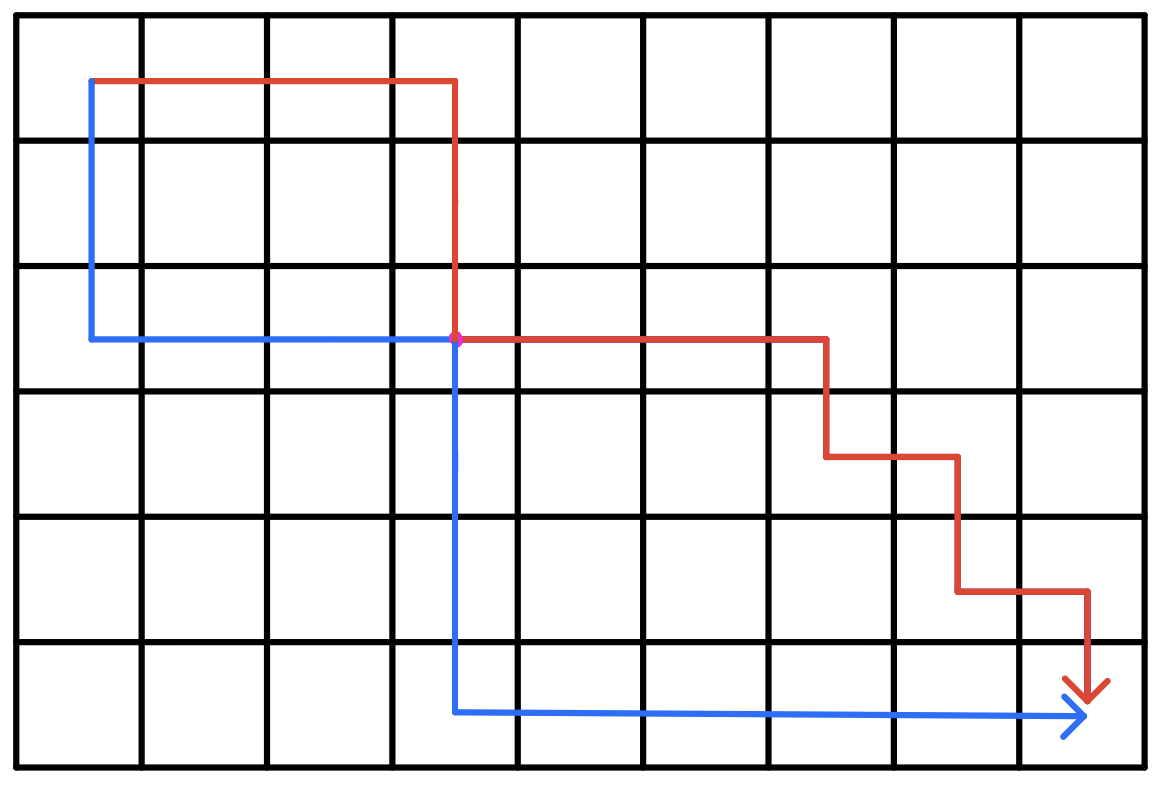
由于方格取数,对于走到相同格子时,只会累加一次格子的价值
于是我们可以使用 贪心 中的 微调法 来进行这部分的证明
对于 重合 的格子,我们必然可以在两条路线中找到额外的一条或两条路线,使得新的路线不发生重合
具体参照下图:
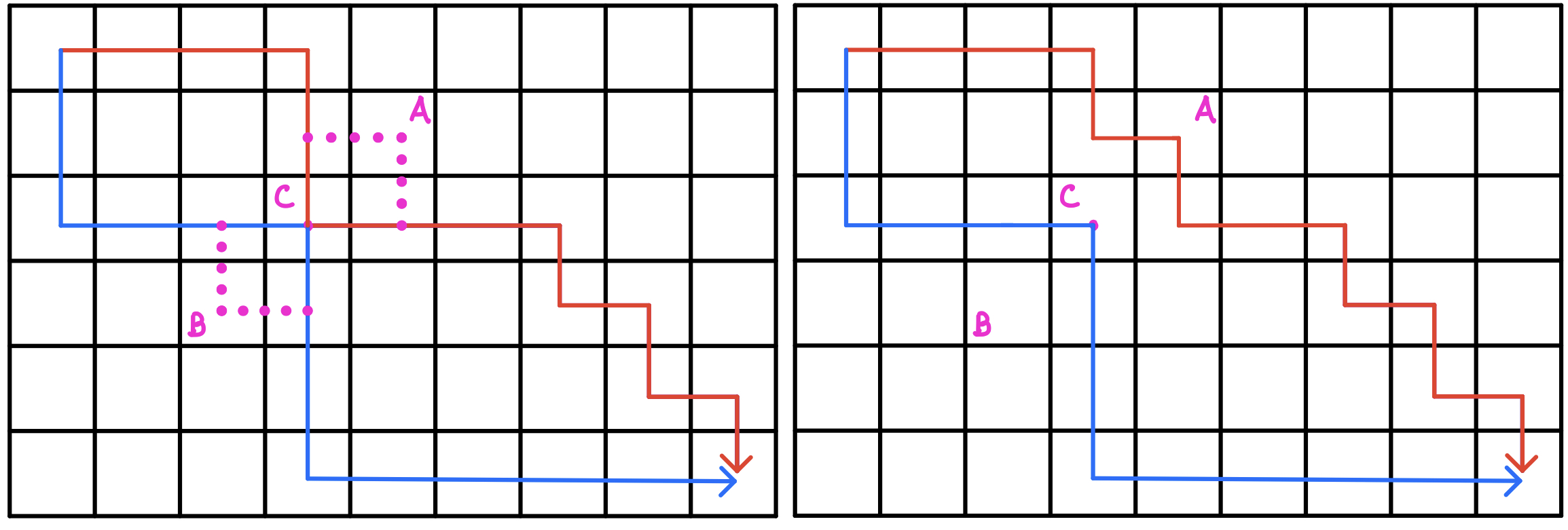
由于原路线是最优解,则必然 w_A=w_B=0,否则最优解路线必然是经过 A 或 B 的
因此,我们可以通过微调其中的一条路线,使之不经过重合点 C,同时路线的总价值没有减少
得证:最优解路线可以是不经过重复路线的
接下来就是完全参照 AcWing 1027. 方格取数 的DP分析了
集合划分
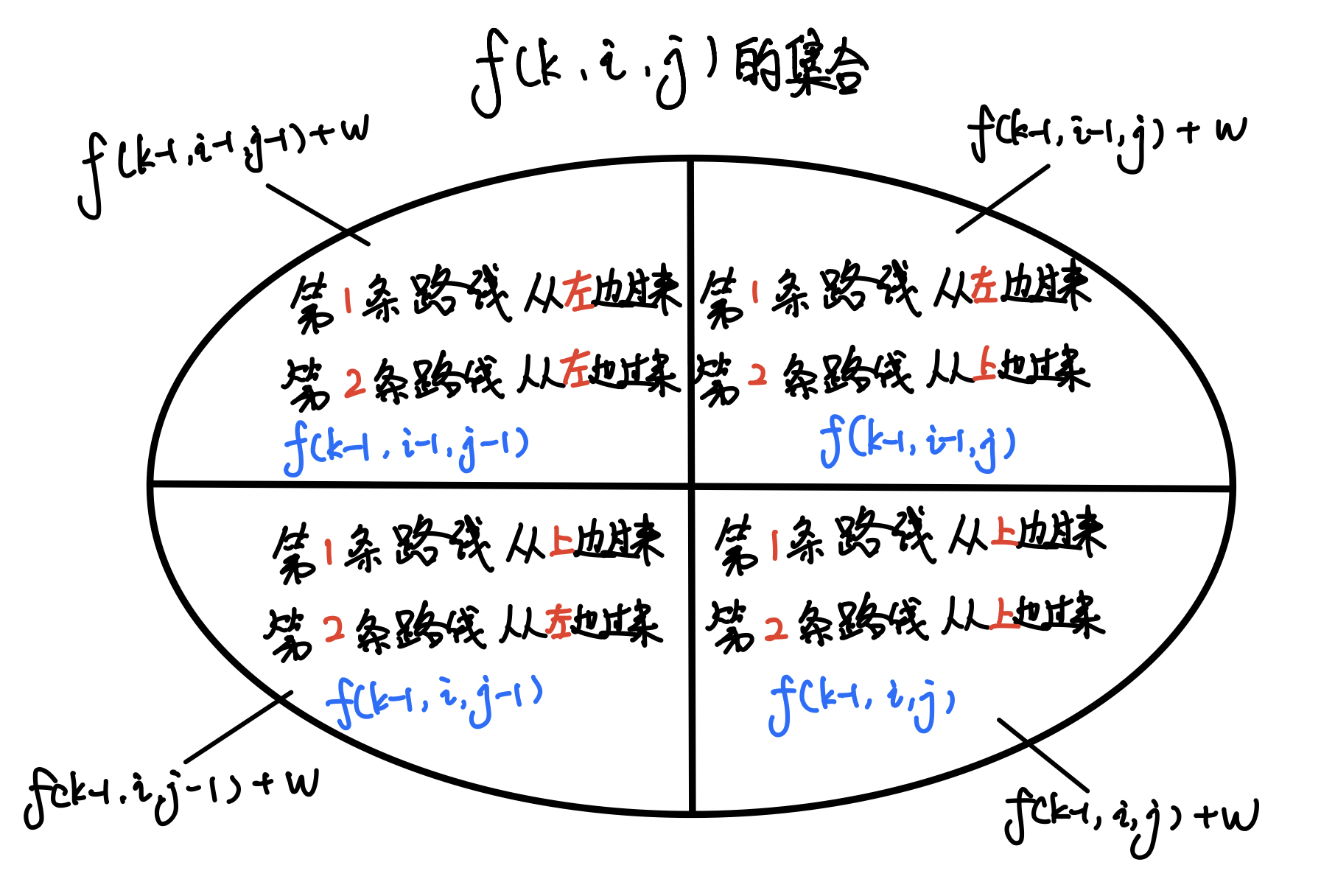
状态的初值: f[2][1][1]
目标的状态: f[n + m][n][m]
#include <bits/stdc++.h>
using namespace std;
const int N = 55;
int n, m;
int w[N][N];
int f[N * 2][N][N];
int main() {
cin >> n >> m;
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++)
cin >> w[i][j];
// 左上角是(1,1),k表示两个小朋友所在位置的x+y的和,最多是n+m
for (int k = 2; k <= n + m; k++)
for (int x1 = 1; x1 <= n; x1++) // 第一个小朋友竖着走的距离
for (int x2 = 1; x2 <= n; x2++) { // 第二个小朋友竖着走的距离
int y1 = k - x1, y2 = k - x2; // 计算横着走的距离
// 不能出界,只走有效的位置
if (y1 < 1 || y1 > m || y2 < 1 || y2 > m) continue;
// 将本位置的数值加上
int &x = f[k][x1][x2];
x = max(x, f[k - 1][x1 - 1][x2] + w[x1][y1]);
x = max(x, f[k - 1][x1 - 1][x2 - 1] + w[x1][y1]);
x = max(x, f[k - 1][x1][x2 - 1] + w[x1][y1]);
x = max(x, f[k - 1][x1][x2] + w[x1][y1]);
// 如果不是重复的位置,还可以继续加上
if (x1 != x2) f[k][x1][x2] += w[x2][y2];
}
// 输出DP的结果
printf("%d\n", f[n + m][n][n]);
return 0;
}
