python/TangDou/AcWing/MiniPath/341.md

AcWing 341. 最优贸易

一、题目描述

C 国有 n 个大城市和 m 条道路，每条道路连接这 n 个城市中的某两个城市。

任意两个城市之间 最多只有一条道路直接相连。

这 m 条道路中有一部分为 单向通行的道路，一部分为 双向通行的道路，双向通行的道路在统计条数时也计为 1 条。

C 国幅员辽阔，各地的资源分布情况各不相同，这就导致了同一种商品在不同城市的价格不一定相同。

但是，同一种商品在同一个城市的买入价和卖出价始终是相同的。

商人阿龙来到 C 国旅游。

当他得知 同一种商品在不同城市的价格可能会不同 这一信息之后，便决定在旅游的同时，利用商品在不同城市中的差价赚一点旅费。

设 C 国 n 个城市的标号从 1∼n，阿龙决定从 1 号城市出发，并最终在 n 号城市结束自己的旅行。

在旅游的过程中，任何城市可以被重复经过多次 ，但不要求经过所有 n 个城市。

阿龙通过这样的贸易方式赚取旅费：他会 选择一个经过的城市买入 他最喜欢的商品——水晶球，并在之后 经过的另一个城市卖出 这个水晶球，用赚取的 差价 当做旅费。

因为阿龙主要是来 C 国旅游，他决定这个贸易 只进行最多一次，当然，在赚不到差价的情况下他就无需进行贸易。

现在给出 n 个城市的水晶球价格，m 条道路的信息（每条道路所连接的两个城市的编号以及该条道路的通行情况）。

请你告诉阿龙，他最多能赚取多少旅费。

注意：本题数据有 加强。

输入格式 第一行包含 2 个正整数 n 和 m，中间用一个空格隔开，分别表示城市的数目和道路的数目。

第二行 n 个正整数，每两个整数之间用一个空格隔开，按标号顺序分别表示这 n 个城市的商品价格。

接下来 m 行，每行有 3 个正整数，x，y，z，每两个整数之间用一个空格隔开。

如果 z=1，表示这条道路是城市 x 到城市 y 之间的单向道路；如果 z=2，表示这条道路为城市 x 和城市 y 之间的双向道路。

输出格式 一个整数，表示答案。

数据范围 1≤n≤100000,1≤m≤500000, 1≤各城市水晶球价格≤100

输入样例：

5 5
4 3 5 6 1
1 2 1
1 4 1
2 3 2
3 5 1
4 5 2

输出样例：

5

二、解题思路

阿龙决定从 1 号城市出发，并最终在 n 号城市结束自己的旅行。

卖完后要回到点n，然而，题目并没有保证所有点都能去到点n,而且，不是所有边都是无向边。

要知道哪些点不能去到点n，可以 反向建图，在这张图以n为起点看能到达哪些点。

分析： 这道题需要建两个图，一个为 正向图 ，一个为 反向图 ，考虑分别跑最短路变形得到dist1数组和dist2数组:

• dist1[i]表示从点1到点i的所有路径上经过的 最小点权
• dist2[i]表示从点n经过反向边到点i的所有路径上经过的 最大点权。

当求出这两个数组后就可以枚举路径上的 中间点i，最终答案就是

\large max(dist2[i]-dis1t[i])

考虑如何通过最短路求出dist数组，常规思路就是 最短路变形，把松弛条件改为：

if(dist1[j] > min(dist1[u], v[j])){
    dist1[j] = min(dist1[u], v[j]);
    q.push({dist1[j], j});
}

理论 上这就没问题了，不过这道题目比较特殊，由于图中 可能出现回路，且dist值是记录 点权的最值 ，在某些情况下是 具有后效性的，如下图：

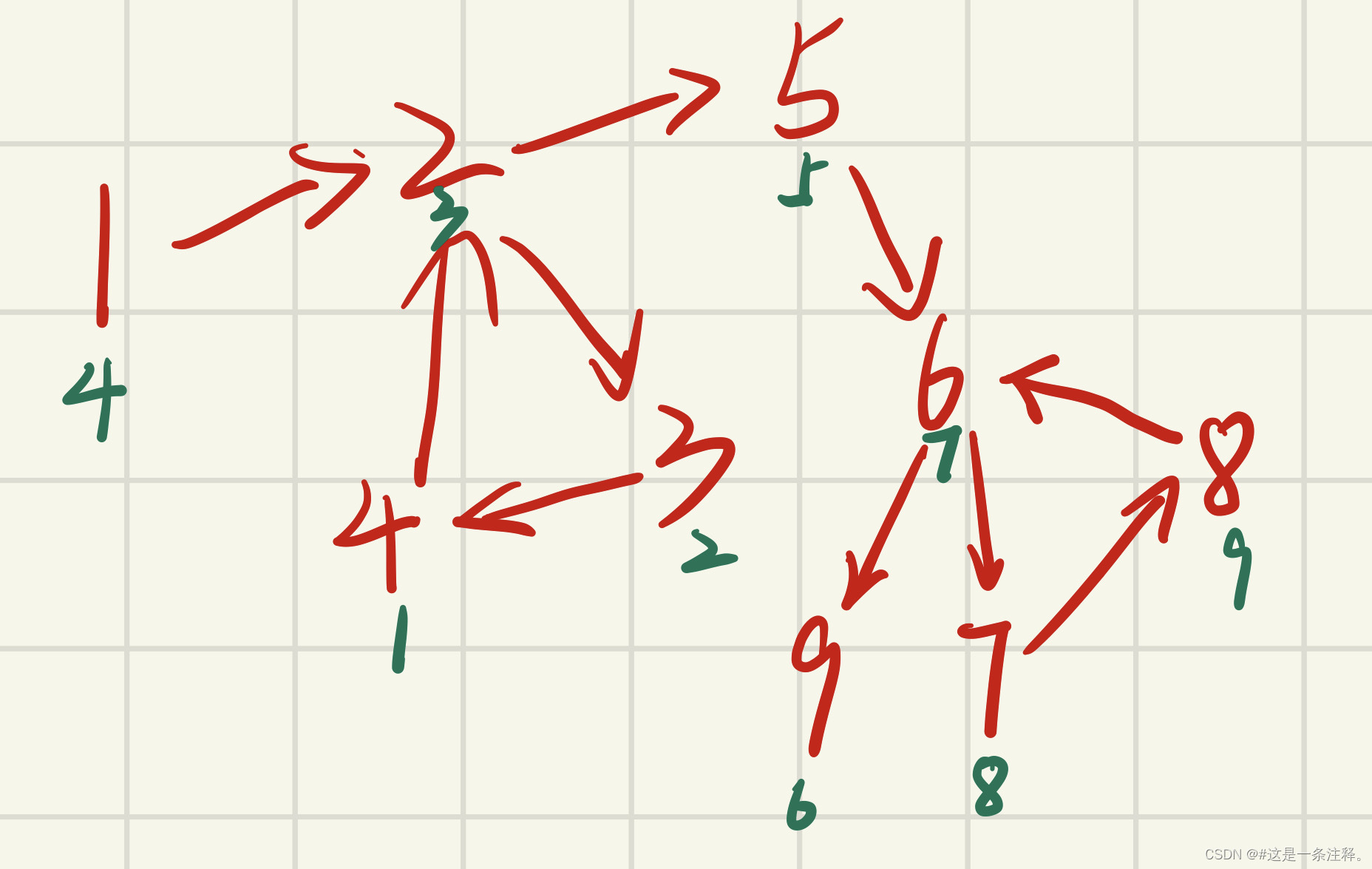
点权 用绿色数字标示在点号下方，可以发现在点2处会经过一个回路再次回到点2，但在这之前点5的dist已经被更新为3了，之后回到点2，由于st[2] == true直接continue，虽然此时dist[2] == 1但却无法把1传递给点5了。

解决方法:dijkstra算法中去掉st的限制，让整个算法不断迭代，直到无法更新导致队空退出循环。

总结 本题用Dijkstra的话，其实已经不是传统意义上的Dijkstra了，因为它允许出边再进入队列！（去掉了st数组 ，因为有环嘛），指望 更无可更，无需再更。这么用Dijkstra其实就不如用SPFA来的直接了，SPFA本身就是更无可更，无需再更。

最大最小值，其实也不是传统最短、最长路的路径累加和，而是类似于DP的思路，一路走来一路维护到达当前点的最大点权和最小点权。严格意义上来讲，采用的Dijkstra或SPFA都不是本身的含义，只是一个协助DP的枚举过程。

Code

#include <bits/stdc++.h>
using namespace std;
typedef pair<int, int> PII;
const int INF = 0x3f3f3f3f;
const int N = 100010, M = 2000010;

int n, m;
int dist1[N], dist2[N];

// 正反建图，传入头数组指针
int h1[N], h2[N], e[M], ne[M], w[M], idx;
void add(int *hh, int a, int b, int c = 0) {
    e[idx] = b, ne[idx] = hh[a], w[idx] = c, hh[a] = idx++;
}
// 每个节点的价值
int v[N];

void dijkstra1() {
    memset(dist1, 0x3f, sizeof dist1);
    priority_queue<PII, vector<PII>, greater<PII>> q;
    dist1[1] = v[1];
    q.push({dist1[1], 1});

    while (q.size()) {
        int u = q.top().second;
        q.pop();

        for (int i = h1[u]; ~i; i = ne[i]) {
            int j = e[i];
            if (dist1[j] > min(dist1[u], v[j])) {
                dist1[j] = min(dist1[u], v[j]);
                q.push({dist1[j], j});
            }
        }
    }
}

void dijkstra2() {
    memset(dist2, -0x3f, sizeof dist2);
    priority_queue<PII> q;
    dist2[n] = v[n];
    q.push({dist2[n], n});

    while (q.size()) {
        int u = q.top().second;
        q.pop();
        for (int i = h2[u]; ~i; i = ne[i]) {
            int j = e[i];
            if (dist2[j] < max(dist2[u], v[j])) {
                dist2[j] = max(dist2[u], v[j]);
                q.push({dist2[j], j});
            }
        }
    }
}

int main() {
    // 正反两张图
    //  Q:为什么要反着建图，用正着的图不行吗？
    //  A:不行啊，因为从n向其它地方走，原来的有向图无法向对面走啊，反着建图就行了
    memset(h1, -1, sizeof h1);
    memset(h2, -1, sizeof h2);

    scanf("%d %d", &n, &m);                          // n个节点，m条边
    for (int i = 1; i <= n; i++) scanf("%d", &v[i]); // 每个节点购买水晶球的金额

    while (m--) {
        int a, b, c;
        scanf("%d %d %d", &a, &b, &c);
        // 不管是单向边，还是双向边，第一条a->b的边肯定跑不了吧

        if (c == 1) { // 单向边
            // 正向图保存单向边
            add(h1, a, b);
            // 反向图保存单向边
            add(h2, b, a);
            // 注意：这可不是在一个图中创建两条来回的边，而是在两个图中创建两个相反的边。
            // 权值呢？没有，为什么呢？因为我们不关心边权，而是关心此节点中水晶球的价格v[i]，这并不是边权,可以理解为点权
        } else { // 双向边
            // 正向图保存双向边
            add(h1, a, b), add(h1, b, a);
            // 反向图保存双向边
            add(h2, a, b), add(h2, b, a);
        }
    }
    // 正向图跑一遍dijkstra
    dijkstra1();
    // 反向图跑一遍dijkstra
    dijkstra2();

    int ans = 0;
    for (int i = 1; i <= n; i++)
        ans = max(dist2[i] - dist1[i], ans);

    printf("%d\n", ans);
    return 0;
}