5.3 KiB
一、题目描述
给出正整数 n 和 k,计算 j(n,k)=k~mod~1+k~mod~2+k~mod~3+…+k~mod~n 的值。
例如 j(5,3)=3~mod~1+3~mod~2+3~mod~3+3~mod~4+3~mod~5=0+1+0+3+3=7。
输入格式
输入仅一行,包含两个整数 n,k。
输出格式
输出仅一行,即 j(n,k)。
数据范围
1≤n,k≤10^9
输入样例:
5 3
输出样例:
7
二、暴力作法
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define endl "\n"
int n, k, ans;
signed main() {
// 通过了 6/10个数据
cin >> n >> k;
for (int i = 1; i <= n; i++) ans += k % i;
cout << ans << endl;
}
三、整除分块
我们先研究一下如下的序列有哪些特点,再结合本题实际给出解题思路:
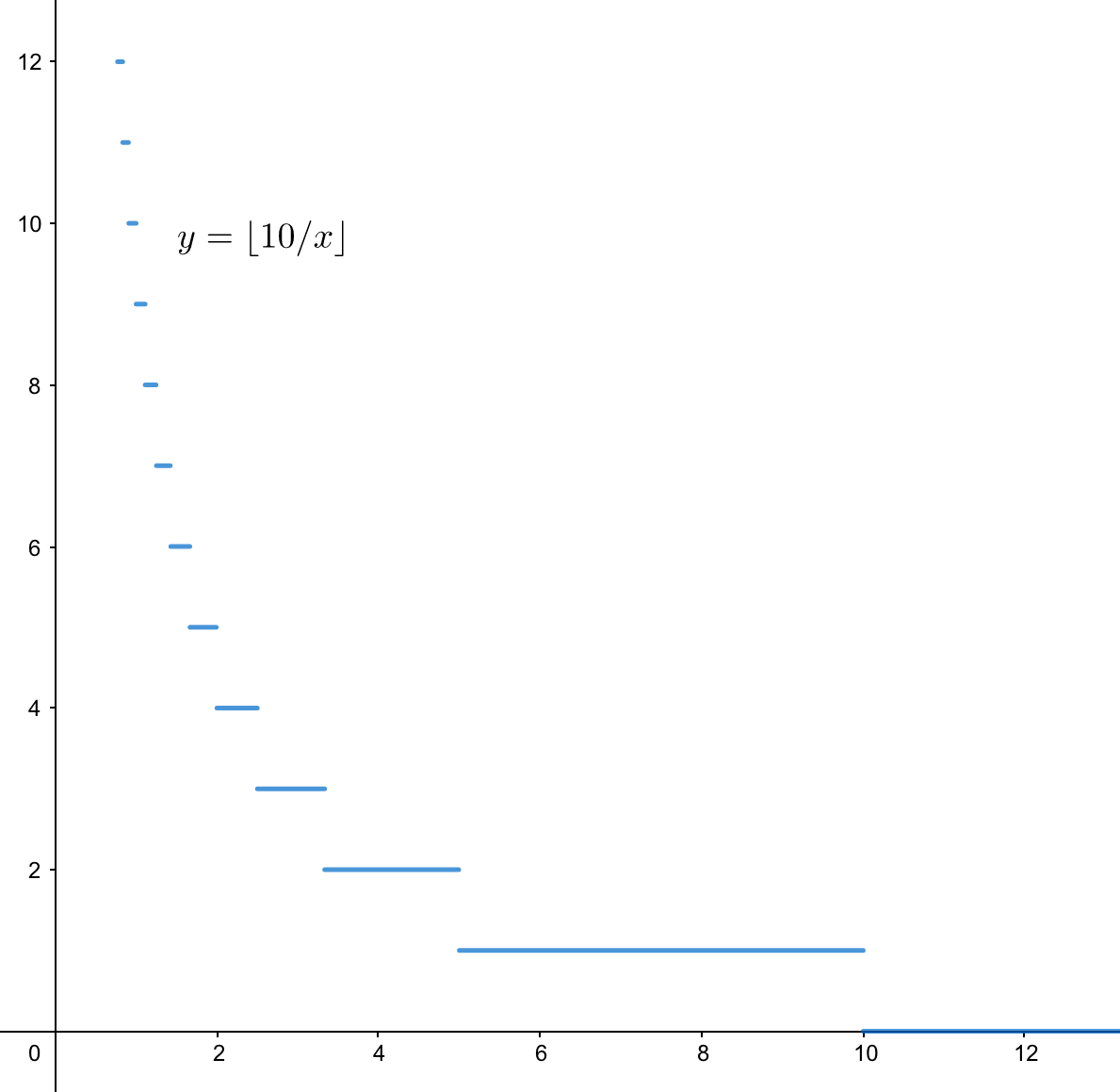
\large \displaystyle f(i)=\lfloor \frac{n}{i} \rfloor ~ (i \in [1,n])注:本题要求的是
[1 \sim n]之内所有数字对数字k取模,我们偏偏不直接研究取模,而是在研究[1 \sim n]之内每个数字被n整除的结果。看来这个结果,与最终目标取模是有关系的,后面的题解中也会证明这一点。
举个例子,n = 5,
$f(1)=5/1=5 \
f(2)=5/2=2 \
f(3)=5/3=1,f(4)=5/4=1,f(5)=5/5=1$
一字排开,得到5,2,1,1,1,相同的分到一个 连续一样的数字段 中,直观一点,写成:[5],[2],[1,1,1]
四、本题题解
题意:给出n,k,求 \displaystyle \sum_{i=1}^{n}k \ mod \ i。
首先取模形式不好处理,根据取模运算定义做 变换:
\large \sum_{i=1}^nk \ mod \ i=\sum_{i=1}^n(k-⌊\frac{k}{i}⌋\cdot i)化简
\large n \cdot k-\sum_{i=1}^n ⌊\frac{k}{i}⌋\cdot i我们发现重点在于求\large \displaystyle \sum_{i=1}^n ⌊\frac{k}{i}⌋ \cdot i。
发现\large \displaystyle ⌊\frac{k}{i}⌋_{i=1}^n的值 呈块状分布(即结果数组分成若干块,每块中值相等),是 整除分块。
1、 块内的累加和是多少?
首先 一个块内部 的答案显然是好求的,设块起点为 l,终点为 r,同时\displaystyle \large ⌊\frac{k}{l}⌋=⌊\frac{k}{l+1}⌋=...=⌊\frac{k}{r}⌋,
累加和是\large \displaystyle ⌊\frac{k}{l}⌋ \cdot \sum_{i=l}^r i。
2、如何根据一个块的起点求块的终点呢?
① 下一个块的起点就是前一个块的终点加1。
② 第一个块的起点位置坐标肯定是1
注:这里说的第一个块的起点,是指最终结果数组中块的下标位置,如上例,就是 序列
5 2 1 1 1序号1 2 3 4 5
③ 如果有办法能通过一个块的起点,找到这个块的终点,那就能确定一个块的范围,我们来研究一下这个办法:
首先由于 块内值 都相同,可以设 \large \displaystyle x= ⌊\frac{k}{l}⌋= ⌊\frac{k}{r}⌋
根据 \displaystyle \large x=⌊\frac{k}{r}⌋ ① \Rightarrow 变形 \Rightarrow \large \displaystyle x \cdot r \leq k \Rightarrow 变形 \Rightarrow \large \displaystyle r \leq ⌊\frac{k}{x}⌋ ②
将\large \displaystyle x=⌊\frac{k}{l}⌋ ① 代入 ②,得\large \displaystyle r \leq ⌊\frac{k}{⌊\frac{k}{l}⌋}⌋,这样就确定了r的最大值。
注:当
k,l确定时,r的上限就已经确定,同时,由于第一起点块的l=1,我们就可以一路向后递推找出所有块的右边界!一旦有了右边界,就可以利用\large \displaystyle ⌊\frac{k}{l}⌋\cdot \sum_{i=l}^ri来快速计算出区间和。
3、时间复杂度【选读】
当 i>\sqrt{n} 时,\large \displaystyle ⌊\frac{k}{i}⌋ \leq \sqrt{n},也就是说原式只有小于 \sqrt{k} 种取值。
注:纯粹的数学思考,除以一个
\geq \sqrt{n}的值,n,k是同一个数据级别\leq 10^9,结果值当然是\leq \sqrt{n}
当i \leq \sqrt{n}时,i只有小于\sqrt{k}种取值,也就是说原式也只有小于\sqrt{k}种取值。
所以最多有 2\sqrt{n} 个块,我们对于每个块可以 O(1) 计算,时间可以通过。
Code
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define endl "\n"
// 数论分块模板题,是很多题的基础,需要背诵
// j(n,k)=k%1+k%2+k%3+…+k%n
int n, k, l, r;
int ans;
signed main() {
cin >> n >> k;
ans = n * k; // 看题解的推导公式
for (l = 1; l <= n; l = r + 1) { // 枚举左端点,每次跳着走,下次的位置就是本次r的位置+1
if (k / l == 0) break; // 1、当k/l=0的时候,显然这段以及后面(有单调性)已经没有贡献了,可以 break。
r = min(k / (k / l), n); // 2、注意右端点和n取个min,因为>n没有贡献了。
ans -= (k / l) * (l + r) * (r - l + 1) / 2; // 等差数列求和:左到右边界内,是公差为1的等差数列,首项+末项 乘以 项数 除以2
}
cout << ans << endl;
}