python

7.9 KiB

Raw Blame History Unescape Escape

This file contains ambiguous Unicode characters that may be confused with others in your current locale. If your use case is intentional and legitimate, you can safely ignore this warning. Use the Escape button to highlight these characters.

`AcWing` `1072` 树的最长路径

一、题目描述

给定一棵树，树中包含 n 个结点（编号1~n）和 n−1 条无向边，每条边都有一个权值。

现在请你找到树中的一条最长路径。

换句话说，要找到一条路径，使得使得路径两端的点的距离最远。

注意：路径中可以只包含一个点。

输入格式 第一行包含整数 n。

接下来 n−1 行，每行包含三个整数 a_i,b_i,c_i，表示点 a_i 和 b_i 之间存在一条权值为 c_i 的边。

输出格式 输出一个整数，表示树的最长路径的长度。

数据范围 1≤n≤10000, 1≤a_i,b_i≤n, −10^5≤c_i≤10^5

输入样例：

输出样例：

二、朴素版本`dfs`【不能`AC`】

朴素dfs: 对每个点求最远点最大距离, 所有结果的max就是结果. 通过 10/16. 然后TLE, 效果不是很理想。

#include <bits/stdc++.h>
using namespace std;

const int N = 10010, M = 20010;
// 　暴力搜索，从每个节点为根出发，遍历整根树，找出距离自己的最大距离,然后每个最大距离取min
//   10/16,其它TLE,无法AC
int n;
int ans; // 树的直径
// 邻接表
int e[M], h[N], idx, w[M], ne[M];
void add(int a, int b, int c = 0) {
    e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx++;
}
int st[N];

void dfs(int u, int sum) {
    st[u] = 1;
    if (sum > ans) ans = sum;
    for (int i = h[u]; ~i; i = ne[i]) {
        int j = e[i];
        if (st[j]) continue; // 不走回头路
        dfs(j, sum + w[i]);
    }
}

int main() {
    // 初始化邻接表
    memset(h, -1, sizeof h);

    cin >> n;
    for (int i = 1; i < n; i++) { // n-1条边
        int a, b, c;
        cin >> a >> b >> c;
        add(a, b, c), add(b, a, c); // 无向图
    }

    // 多次dfs,是TLE的罪魁祸首
    for (int i = 1; i <= n; i++) {
        memset(st, 0, sizeof st);
        dfs(i, 0);
    }

    // 输出结果
    printf("%d", ans);
    return 0;
}

三、两次`dfs`解法【不能`AC`】

优点：思路简单

缺点：只适用于不带负边的树

此题目中的第15组数据，可以HACK掉这种作法(此组数据中带有负权边)

算法：从任意点a出发, 找到距离a最远的点t1, 然后从t1出发, 找到距离t1最远的点t2,t1和t2的距离即为我们要找到结果.

黄海注：在AcWing 1073中，没有出现边权是负值的情况，所以两遍dfs大法好用 : 传送门

这里我就不赘述证明了，想看证明的同学可以移步洛谷里面一个题的题解，里面有证明: 传送门,或者看一下yxc本题的视频教程。

通过了 14/16个数据,剩余两个测试点，居然是WA,真是，唉~

#include <bits/stdc++.h>

using namespace std;

const int N = 10010, M = 20010;

int ans; // 保存最长路径
int t;   // 保存找到的最远点
int n;

// 邻接表
int e[M], h[N], idx, w[M], ne[M];
void add(int a, int b, int c = 0) {
    e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx++;
}
int st[N];

void dfs(int u, int sum) {
    st[u] = 1;
    if (sum > ans) {
        ans = sum; // 记录最大距离
        t = u;     // 记录最远的点t1
    }
    for (int i = h[u]; ~i; i = ne[i]) {
        int j = e[i];
        if (st[j]) continue;
        dfs(j, sum + w[i]);
    }
}

int main() {
    memset(h, -1, sizeof h);
    cin >> n;
    for (int i = 1; i < n; i++) {
        int a, b, c;
        cin >> a >> b >> c;
        add(a, b, c), add(b, a, c);
    }
    memset(st, 0, sizeof st);
    dfs(1, 0); // 先找到点距离点1最远的点t1

    memset(st, 0, sizeof st);
    dfs(t, 0); // 找到距离点t1->t2最远的点t1

    printf("%d", ans);
    return 0;
}

四、最长+次长解法【终极解法】

树的最长路径 ，也称为树的直径 ,直径 不唯一

我们知道：树上 任意两点 的路径是唯一确定的，因此我们可以暴力枚举起点和终点找出最长路径

如果这样做的话，我们来思考一下时间复杂度：

枚举起点和终点 — O(n^2) 找出两点之间的路径长度 — O(logn)

但是光是枚举起点和终点，时间复杂度 就直接拉满了，显然这种做法不可取。

既然这 O(n^2) 条路径不能一一枚举，那么有什么方式可以把他们 分类枚举 呢？

考虑换一种 枚举方式：枚举路径的 起点和终点 → 枚举路径的 中间节点

注：枚举中间节点非常妙，因为树节点只有n个，全遍历一遍也没啥问题，怕就怕双重循环的两两一组。如此，就成功的将双重循环O(N^2)时间复杂度降为O(N)的时间复杂度。方法就是在遍历过程中，努力构建关于当前节点u的多重信息，然后用这些信息去组装出直径最大值,果然有dp的味道在里面~

我们先讨论一下，对于给定拓扑结构的树里的任意节点，经过它的路径有哪些：

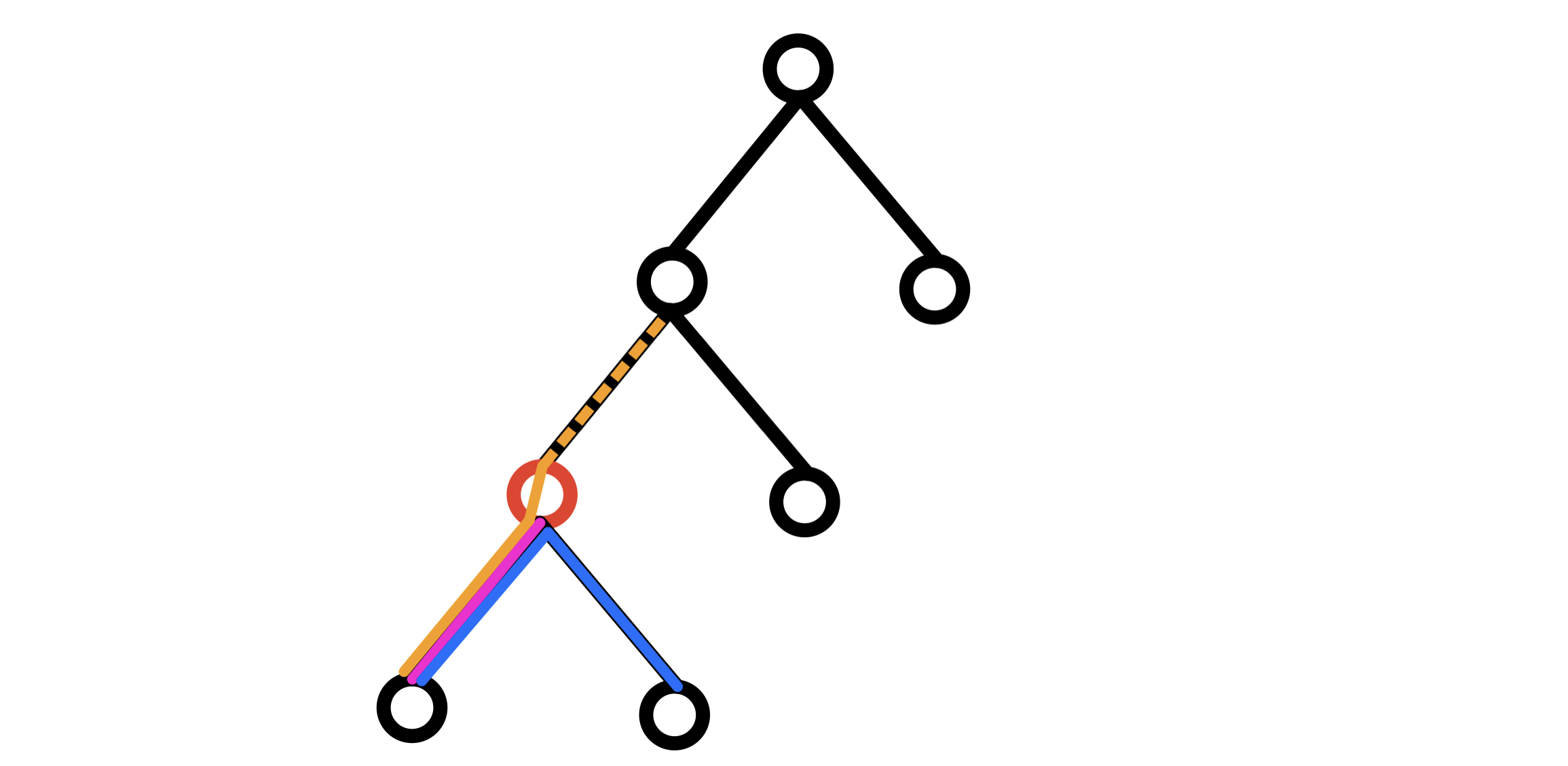
观察 红色节点【本质上就是对于树中的任意节点均同此理】，经过它的路径有：

以其 子树中的某个节点 作为起点，以它作为终点的 粉色路径
以其 子树中的某个节点 作为起点，以 子树中的某个节点 作为终点的 蓝色路径
以其 子树中的某个节点 作为起点，以 非其子树的节点 作为终点的 橙色路径

对于第 1 种情况，可以 直接递归处理其子树，找出到当前子树根节点最长的路径长度即可 对于第 2 种情况，在处理第 1 种情况时，顺便找出 1 类路径的 次长路径，再把最长和次长拼在一起，就是第 2 种情况对于第 3 种情况，可以把它归类为其 祖先节点 的第 1,2 种情况，让其 祖先节点 去处理即可

实现代码

#include <bits/stdc++.h>

using namespace std;

const int N = 10010; // 点数上限
const int M = N * 2; // 边数上限
int n;
int ans;
int d1[N], d2[N]; // 最长，次长
int st[N];
int h[N], e[M], w[M], ne[M], idx;
void add(int a, int b, int c) {
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++;
}

void dfs(int u) {
    st[u] = 1;
    for (int i = h[u]; ~i; i = ne[i]) {
        int j = e[i];
        if (st[j]) continue;

        // 走j子树,完成后，j子树中每个节点的d1[j],d2[j]都已经准备好，u节点可以直接利用
        dfs(j);

        // d1[u]:最长路径,d2[u]:次长路径
        if (d1[j] + w[i] >= d1[u])
            d2[u] = d1[u], d1[u] = d1[j] + w[i]; // 最长路转移
        else if (d1[j] + w[i] > d2[u])
            d2[u] = d1[j] + w[i]; // 次长路转移
    }
    // 更新结果
    ans = max(ans, d1[u] + d2[u]);
}

int main() {
    cin >> n;
    // 初始化邻接表
    memset(h, -1, sizeof h);
    for (int i = 1; i < n; i++) {
        int a, b, c;
        cin >> a >> b >> c;
        add(a, b, c), add(b, a, c);
    }
    // 任选一个点作为根节点
    dfs(1);
    // 输出答案
    printf("%d", ans);
    return 0;
}

7.9 KiB Raw Blame History Unescape Escape

AcWing 1072 树的最长路径