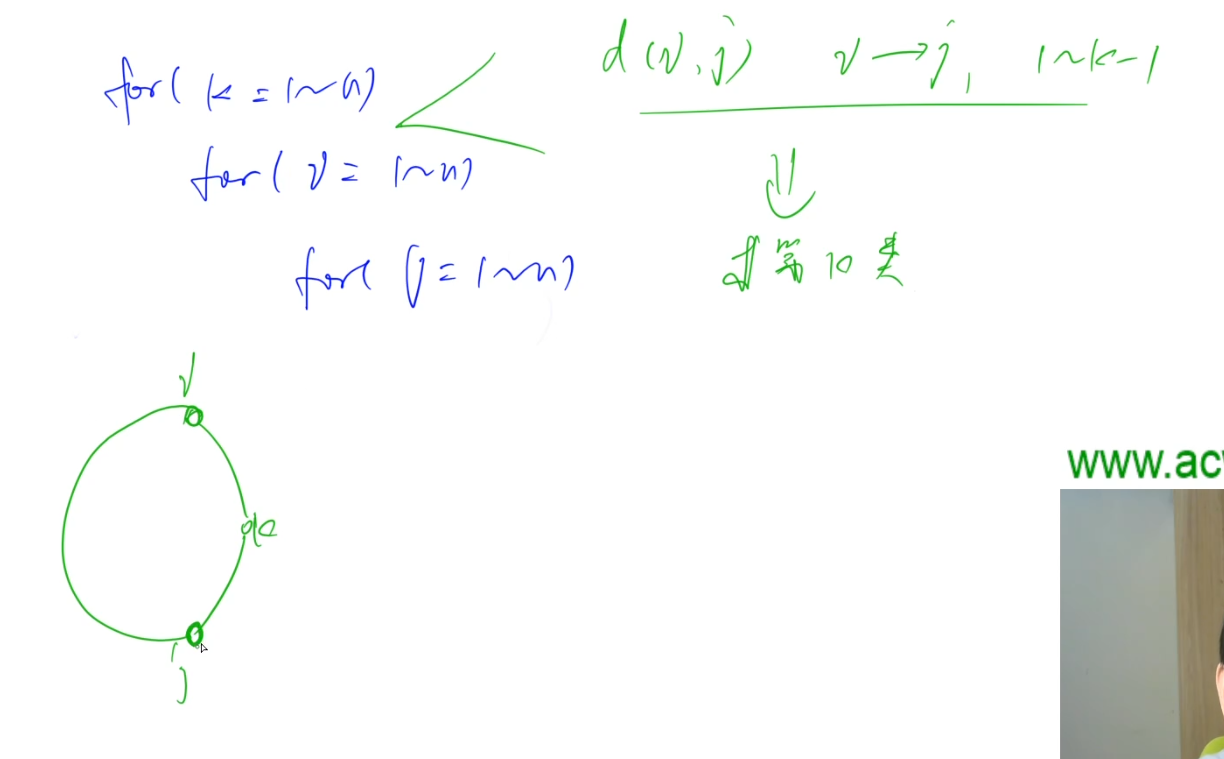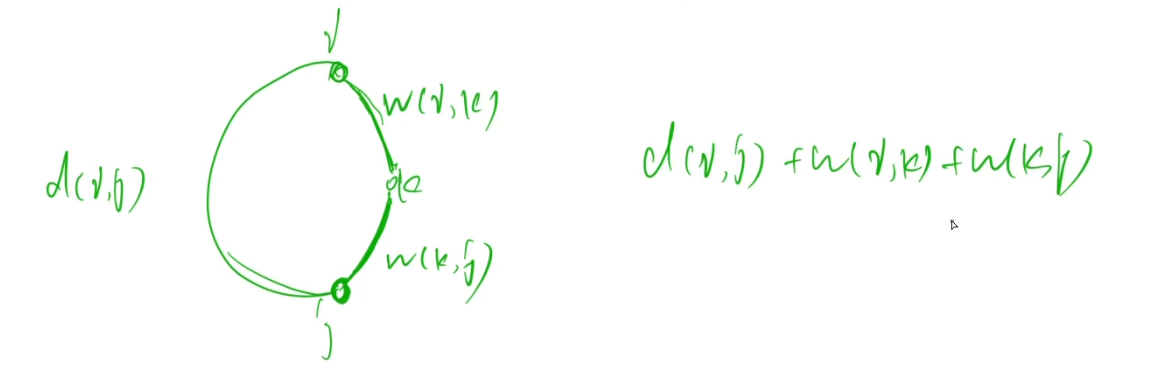python/TangDou/AcWing_TiGao/T3/Floyd/344.md

AcWing 344. 观光之旅

一、题目描述

给定一张无向图，求图中一个 至少包含 3 个点 的环，环上的节点不重复，并且环上的边的长度之和最小。

该问题称为 无向图的最小环问题。

你需要输出最小环的方案，若最小环不唯一，输出任意一个均可。

输入格式 第一行包含两个整数 N 和 M，表示无向图有 N 个点，M 条边。

接下来 M 行，每行包含三个整数 u，v，l，表示点 u 和点 v 之间有一条边，边长为 l。

输出格式 输出占一行，包含最小环的所有节点（按顺序输出），如果不存在则输出 No solution.。

数据范围 1≤N≤100,1≤M≤10000,1≤l<500

输入样例：

5 7
1 4 1
1 3 300
3 1 10
1 2 16
2 3 100
2 5 15
5 3 20

输出样例：

1 3 5 2

二、算法思路

最优化问题，可以从集合角度来思考，从集合角度来思考的一个好处就是：不容易丢东西。

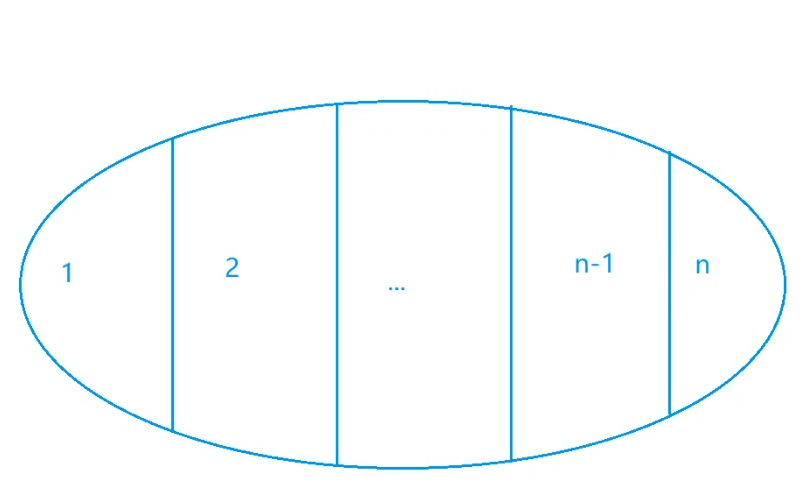
按环上编号最大点的编号为分类依据，分完类之后，只需要分别求一个每一类的最小值，然后PK一下求min所有最小值就是答案。

每一类的最小值怎么求呢？我们来加快一下floyd的过程：

for(int k=1;k<=n;k++) //K是要插入的点,dis[i][j]数组相当是知道了i~j的只经过1~k-1这些点的最小路径
    //此时在这个地方可以求第k类。从某个点连接到k
  for(int i=1;i<=n;i++) 
    for(int j=1;j<=n;j++){

    }

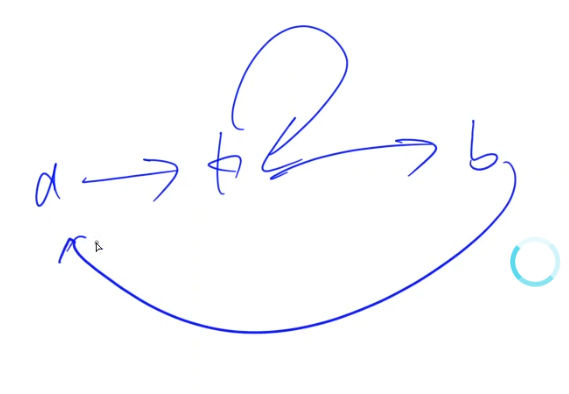
枚举一下所有的点对(i,j),固定了(i,j)之后，那么i-k,k-j的长度都是固定的。

本题还有一个难点，就是floyd需要记录方案，其实就是求一下d[i][j]是由哪个中间点转移过来的。

k的含义：不算i,j的情况下，中间点里的最大值。

Code

#include <bits/stdc++.h>

using namespace std;
const int N = 110, INF = 0x3f3f3f3f;
int n, m;
int g[N][N], dis[N][N];
vector<int> path;
int mid[N][N];
int ans = INF;

// i->j之间的最短路径中途经点有哪些
void get_path(int i, int j) {
    int k = mid[i][j]; // 获取中间转移点
    if (!k) return;    // 如果i,j之间没有中间点，停止
    get_path(i, k);    // 递归前半段
    path.push_back(k); // 记录k节点
    get_path(k, j);    // 递归后半段
}

int main() {
    // n个顶点，m条边
    cin >> n >> m;

    // 初始化邻接矩阵
    memset(g, 0x3f, sizeof g);
    for (int i = 1; i <= n; i++) g[i][i] = 0; // 邻接矩阵，自己到自己距离是0

    while (m--) {
        int a, b, c;
        cin >> a >> b >> c;
        g[a][b] = g[b][a] = min(g[a][b], c); // 求最短路之类，(a,b)之间多条边输入只保留最短边
    }

    // 把原始地图复制出来到生成最短距离dis
    memcpy(dis, g, sizeof dis);

    for (int k = 1; k <= n; k++) { // 枚举每一个引入点k来连接缩短i,j的距离
        /*
        Q1:为什么循环的时候i和j都需要小于k?
        A:为了避免经过相同的点，比如i == k时，三个点就变成两个点了。
        其实循环到n也是可以的，不过当i, j, k中有两个相同时就要continue一下

        Q2:为什么非得把DP的这段代码嵌入到Floyd的整体代码中，不能先Floyd后再进行DP吗？
        A:是不可以的。因为在进行插入节点号为k时，其实dis[i][j]中记录的是1~k-1插点后的最小距离，
        而不是全部插入点后的最短距离。
        */
        for (int i = 1; i < k; i++)
            for (int j = i + 1; j < k; j++)
                if (g[i][k] + g[k][j] < ans - dis[i][j]) { // 减法防止爆INT
                    ans = dis[i][j] + g[i][k] + g[k][j];
                    // 找到更小的环，需要记录路径,并且要求: 最小环的所有节点（按顺序输出）
                    //  顺序
                    //  1. 上面的i,j枚举逻辑是j>i,所以i是第一个
                    //  2. i->j 中间的路线不明，需要用get_path进行查询出i->j的最短路径怎么走,当然，也是在<k的范围内的
                    //  3. 记录j
                    //  4. 记录k
                    path.clear();
                    path.push_back(i);
                    get_path(i, j); // i是怎么到达j的？就是问dis[i][j]是怎么获取到的，这是在求最短路径过程中的一个路径记录问题
                    path.push_back(j);
                    path.push_back(k);
                }

        // 正常floyd
        for (int i = 1; i <= n; i++)
            for (int j = 1; j <= n; j++)
                if (dis[i][j] > dis[i][k] + dis[k][j]) {
                    dis[i][j] = dis[i][k] + dis[k][j];
                    mid[i][j] = k; // 记录路径i->j 是通过k进行转移的
                }
    }

    if (ans == INF)
        puts("No solution.");
    else
        for (int i = 0; i < path.size(); i++) cout << path[i] << ' ';

    return 0;
}