4.0 KiB
一、题目描述
给出一个 有向无环的连通图,起点为 1 ,终点为 N,每条边都有一个长度。
数据保证从起点出发能够到达图中所有的点,图中所有的点也都能够到达终点。
绿豆蛙从起点出发,走向终点。
到达每一个顶点时,如果有 K 条离开该点的道路,绿豆蛙可以选择任意一条道路离开该点,并且走向每条路的概率为 1/K。
现在绿豆蛙想知道,从起点走到终点所经过的路径总长度的 期望 是多少?
输入格式
第一行: 两个整数 N,M,代表图中有 N 个点、M 条边。
第二行到第 1+M 行: 每行 3 个整数 a,b,c,代表从 a 到 b 有一条长度为 c 的有向边。
输出格式 输出从起点到终点路径总长度的 期望值,结果四舍五入保留两位小数。
数据范围
1≤N≤10^5,1≤M≤2N
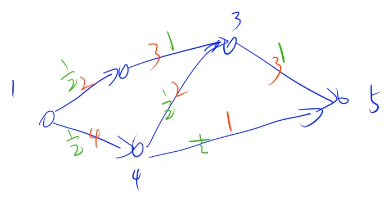
输入样例:
4 4
1 2 1
1 3 2
2 3 3
3 4 4
输出样例:
7.00
二、数学期望
期望的起点一般都是唯一的,终点一般都是不唯一的。
所以,一般我们喜欢从终点倒推。
f(i):从i跳到N的期望长度。边界f(N)=0
答案:f(1)
首先明白一点:到达某个结果的期望值 = 这个结果 * 从起始状态到这个状态的概率
什么意思呢?
如图:
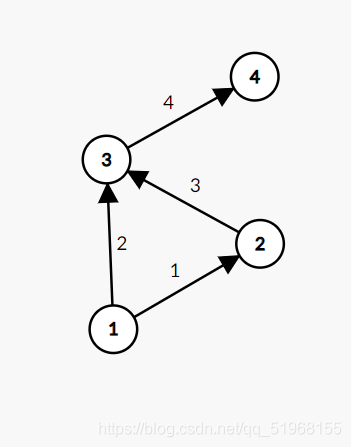
我们计算从1号点到3号点的期望距离
路径1. \displaystyle 1 \rightarrow 3:E_1=2×\frac{1}{2}=1
路径2. \displaystyle 1 \rightarrow 2 \rightarrow 3:E_2=1×\frac{1}{2}+3×\frac{1}{2}×1=2
这里路径2中从1到2概率为\displaystyle \frac{1}{2},但单看从2到3概率就是1,但是从1到3那就是从(1到2的概率)\displaystyle \frac{1}{2}×1(2到3的概率)=\displaystyle \frac{1}{2}。
所以从 点1 到 点3 的数学期望值=1+2=3
总结 ① 概率是叠乘的 ② 概率计算出来后,需要乘上边权值,做为本边权的贡献值 ③ 所有贡献值累加和就是期望
有向无环图
题意:给定一个DAG,求路径和。
由题意知,题目中的K就是每个点的出度。
然后,又由题意知,最后一个点,它没有出度,而到自己的距离为0,即状态已经确定。
用前向星存图,从第一个点开始
DFS,每次枚举它所连的边,并把边的边权 (w[i])加上,最后除以它的出度即可。
方程: $dp[n]=0 \ dp[i]+=(dp[son[i]]+e[son[i]].val)/out[i]$
其中,
son[i]是i所连得边,e是前向星,val是边权,out[i]是i的出度。
Code
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10, M = N << 1;
int n, m;
int h[N], e[M], ne[M], w[M], idx;
int out[N];
double f[N];
void add(int a, int b, int c) {
e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++;
}
double dfs(int u) {
if (f[u] >= 0) return f[u]; // 如果u点计算过,记忆化搜索返回结果值
f[u] = 0; // 初始化为0,准备开始填充
for (int i = h[u]; ~i; i = ne[i]) {
int j = e[i];
f[u] += (w[i] + dfs(j)) / out[u];
}
return f[u];
}
int main() {
memset(h, -1, sizeof h);
cin >> n >> m;
while (m--) {
int a, b, c;
cin >> a >> b >> c;
add(a, b, c);
out[a]++;
}
memset(f, -1, sizeof f);
printf("%.2lf\n", dfs(1));
return 0;
}