|
|
## $Dijkstra$算法专题
|
|
|
|
|
|
### 一、解决的问题
|
|
|
计算从 **源** 到所有其他各顶点的最短路径长度。这里的长度是指路上各边权之和。这个问题通常称为单源最短路径问题。
|
|
|
|
|
|
### 二、算法原理
|
|
|
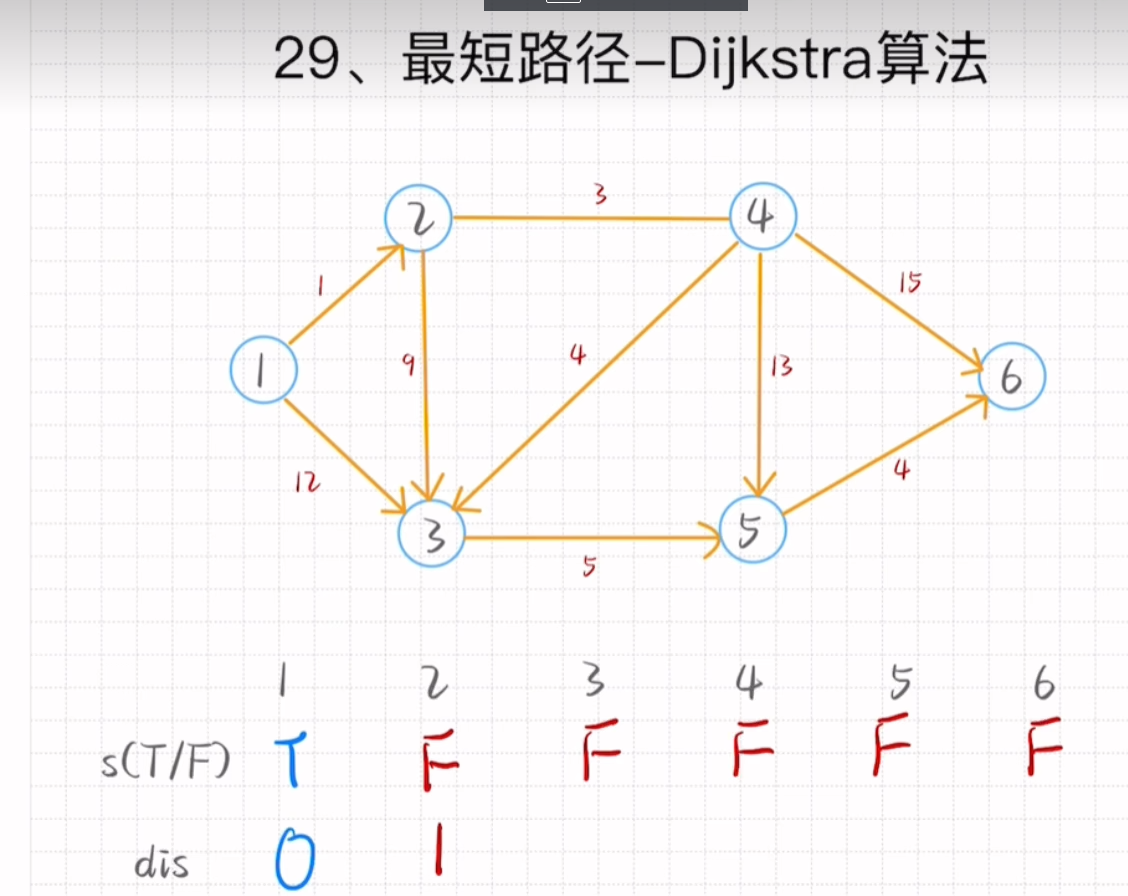
|
|
|
|
|
|
> **视频讲解** : **[【5分钟搞定$Dijkstra$算法】](https://www.bilibili.com/video/BV1ha4y1T7om)**
|
|
|
|
|
|
### 三、题单
|
|
|
#### 【模板题】[$AcWing$ $850$. $Dijkstra$求最短路 $II$](https://www.acwing.com/problem/content/description/852/)
|
|
|
|
|
|
输入样例
|
|
|
```cpp {.line-numbers}
|
|
|
3 3
|
|
|
1 2 2
|
|
|
2 3 1
|
|
|
1 3 4
|
|
|
```
|
|
|
输出样例
|
|
|
```cpp {.line-numbers}
|
|
|
3
|
|
|
```
|
|
|
**$Code$**
|
|
|
```cpp {.line-numbers}
|
|
|
#include <bits/stdc++.h>
|
|
|
|
|
|
using namespace std;
|
|
|
typedef pair<int, int> PII;
|
|
|
const int INF = 0x3f3f3f3f;
|
|
|
const int N = 150010, M = N << 1;
|
|
|
|
|
|
int st[N];
|
|
|
int dis[N]; // 距离数组
|
|
|
|
|
|
// 邻接表
|
|
|
int e[M], h[N], idx, w[M], ne[M];
|
|
|
void add(int a, int b, int c) {
|
|
|
e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx++;
|
|
|
}
|
|
|
|
|
|
int n, m;
|
|
|
int dijkstra() {
|
|
|
memset(dis, 0x3f, sizeof dis);
|
|
|
dis[1] = 0;
|
|
|
priority_queue<PII, vector<PII>, greater<PII>> q; // 小顶堆
|
|
|
q.push({0, 1});
|
|
|
|
|
|
while (q.size()) {
|
|
|
PII t = q.top();
|
|
|
q.pop();
|
|
|
int u = t.second;
|
|
|
if (!st[u]) {
|
|
|
st[u] = 1;
|
|
|
for (int i = h[u]; ~i; i = ne[i]) {
|
|
|
int v = e[i];
|
|
|
if (dis[v] > dis[u] + w[i]) {
|
|
|
dis[v] = dis[u] + w[i];
|
|
|
q.push({dis[v], v});
|
|
|
}
|
|
|
}
|
|
|
}
|
|
|
}
|
|
|
if (dis[n] == INF) return -1;
|
|
|
return dis[n];
|
|
|
}
|
|
|
int main() {
|
|
|
cin >> n >> m;
|
|
|
memset(h, -1, sizeof h);
|
|
|
while (m--) {
|
|
|
int a, b, c;
|
|
|
cin >> a >> b >> c;
|
|
|
add(a, b, c);
|
|
|
}
|
|
|
printf("%d\n", dijkstra());
|
|
|
return 0;
|
|
|
}
|
|
|
```
|
|
|
|
|
|
### [$AcWing$ $1129$. 热浪](https://www.acwing.com/problem/content/description/1131/)
|
|
|
与模板相比,只是起点和终点是输入的,其它无区别。
|
|
|
|
|
|
**输入样例**:
|
|
|
```cpp {.line-numbers}
|
|
|
7 11 5 4
|
|
|
2 4 2
|
|
|
1 4 3
|
|
|
7 2 2
|
|
|
3 4 3
|
|
|
5 7 5
|
|
|
7 3 3
|
|
|
6 1 1
|
|
|
6 3 4
|
|
|
2 4 3
|
|
|
5 6 3
|
|
|
7 2 1
|
|
|
```
|
|
|
|
|
|
**输出样例**:
|
|
|
```cpp {.line-numbers}
|
|
|
7
|
|
|
```
|
|
|
|
|
|
|
|
|
**$Code$**
|
|
|
```cpp {.line-numbers}
|
|
|
#include <bits/stdc++.h>
|
|
|
using namespace std;
|
|
|
const int N = 2510;
|
|
|
const int M = 6200 * 2 + 10;
|
|
|
|
|
|
typedef pair<int, int> PII;
|
|
|
|
|
|
int h[N], w[M], e[M], ne[M], idx;
|
|
|
bool st[N];
|
|
|
int dis[N];
|
|
|
|
|
|
void add(int a, int b, int c) {
|
|
|
e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx++;
|
|
|
}
|
|
|
|
|
|
int n, m, S, T;
|
|
|
|
|
|
int dijkstra() {
|
|
|
memset(dis, 0x3f, sizeof dis);
|
|
|
dis[S] = 0;
|
|
|
|
|
|
priority_queue<PII, vector<PII>, greater<PII>> q;
|
|
|
q.push({0, S});
|
|
|
while (q.size()) {
|
|
|
PII t = q.top();
|
|
|
q.pop();
|
|
|
int u = t.second;
|
|
|
if (st[u]) continue;
|
|
|
st[u] = true;
|
|
|
for (int i = h[u]; ~i; i = ne[i]) {
|
|
|
int v = e[i];
|
|
|
if (dis[v] > dis[u] + w[i]) {
|
|
|
dis[v] = dis[u] + w[i];
|
|
|
q.push({dis[v], v});
|
|
|
}
|
|
|
}
|
|
|
}
|
|
|
return dis[T];
|
|
|
}
|
|
|
|
|
|
int main() {
|
|
|
cin >> n >> m >> S >> T;
|
|
|
memset(h, -1, sizeof h);
|
|
|
|
|
|
while (m--) {
|
|
|
int a, b, c;
|
|
|
cin >> a >> b >> c;
|
|
|
add(a, b, c), add(b, a, c);
|
|
|
}
|
|
|
printf("%d\n", dijkstra());
|
|
|
return 0;
|
|
|
}
|
|
|
```
|
|
|
|
|
|
#### [$AcWing$ $1128$. 信使](https://www.acwing.com/problem/content/1130/)
|
|
|
**总结**:从$1$号哨所出发,计算出到每个哨所的最短路径,所以最短路径中最长的,表示需要的最少时间,是一个最短路径模板+思维问题。
|
|
|
|
|
|
**输入样例**:
|
|
|
```cpp {.line-numbers}
|
|
|
4 4
|
|
|
1 2 4
|
|
|
2 3 7
|
|
|
2 4 1
|
|
|
3 4 6
|
|
|
```
|
|
|
|
|
|
**输出样例**:
|
|
|
```cpp {.line-numbers}
|
|
|
11
|
|
|
```
|
|
|
|
|
|
**$Code$**
|
|
|
|
|
|
```cpp {.line-numbers}
|
|
|
#include <bits/stdc++.h>
|
|
|
using namespace std;
|
|
|
typedef pair<int, int> PII;
|
|
|
const int INF = 0x3f3f3f3f;
|
|
|
const int N = 110;
|
|
|
const int M = 2 * 210; // 无向图,需要开二倍的数组长度!
|
|
|
|
|
|
int n, m;
|
|
|
int h[N], e[M], w[M], ne[M], idx;
|
|
|
void add(int a, int b, int c) {
|
|
|
e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++;
|
|
|
}
|
|
|
int dis[N];
|
|
|
bool st[N];
|
|
|
|
|
|
int dijkstra() {
|
|
|
memset(dis, 0x3f, sizeof dis);
|
|
|
dis[1] = 0;
|
|
|
|
|
|
priority_queue<PII, vector<PII>, greater<int>> q;
|
|
|
q.push({0, 1});
|
|
|
|
|
|
while (q.size()) {
|
|
|
PII t = q.top();
|
|
|
q.pop();
|
|
|
int u = t.second;
|
|
|
if (st[u]) continue;
|
|
|
st[u] = true;
|
|
|
|
|
|
for (int i = h[u]; ~i; i = ne[i]) {
|
|
|
int v = e[i];
|
|
|
if (dis[v] > dis[u] + w[i]) {
|
|
|
dis[v] = dis[u] + w[i];
|
|
|
q.push({dis[v], v});
|
|
|
}
|
|
|
}
|
|
|
}
|
|
|
int mx = 0;
|
|
|
for (int i = 1; i <= n; i++) {
|
|
|
if (dis[i] == INF) return -1;
|
|
|
mx = max(mx, dis[i]);
|
|
|
}
|
|
|
return mx;
|
|
|
}
|
|
|
int main() {
|
|
|
memset(h, -1, sizeof h);
|
|
|
cin >> n >> m;
|
|
|
while (m--) {
|
|
|
int a, b, c;
|
|
|
cin >> a >> b >> c;
|
|
|
add(a, b, c), add(b, a, c);
|
|
|
}
|
|
|
printf("%d\n", dijkstra());
|
|
|
return 0;
|
|
|
}
|
|
|
|
|
|
```
|
|
|
|
|
|
#### [$AcWing$ $1127$. 香甜的黄油](https://www.acwing.com/problem/content/1129/)
|
|
|
|
|
|
**总结**:本题不是有固定的起点和终点,是起点不一定是哪个。我们需要枚举每一个点做为起点,然后计算每个点作为起点时,消耗的总的边权和,也是代价值。最后比较一下最小的代价值,可以找出哪个点作为起点是最好的选择。
|
|
|
|
|
|
**输入样例**:
|
|
|
```cpp {.line-numbers}
|
|
|
3 4 5
|
|
|
2
|
|
|
3
|
|
|
4
|
|
|
1 2 1
|
|
|
1 3 5
|
|
|
2 3 7
|
|
|
2 4 3
|
|
|
3 4 5
|
|
|
```
|
|
|
|
|
|
**输出样例**:
|
|
|
```cpp {.line-numbers}
|
|
|
8
|
|
|
```
|
|
|
|
|
|
**$Code$**
|
|
|
```cpp {.line-numbers}
|
|
|
#include <bits/stdc++.h>
|
|
|
|
|
|
using namespace std;
|
|
|
typedef pair<int, int> PII;
|
|
|
const int N = 810; // 牧场数 上限800
|
|
|
const int M = 3000; // 牧场间道路数 上限1450,无向图开双倍
|
|
|
const int INF = 0x3f3f3f3f;
|
|
|
// 邻接表
|
|
|
int h[N], e[M], w[M], ne[M], idx;
|
|
|
void add(int a, int b, int c) {
|
|
|
e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++;
|
|
|
}
|
|
|
|
|
|
int n, p, m; // 三个数:奶牛数 ,牧场数 ,牧场间道路数
|
|
|
int id[N]; // 每只奶牛在哪个牧场
|
|
|
int dis[N]; // 记录起点到任意点的最短路径
|
|
|
bool st[N]; // 标识每个牧场是否入过队列
|
|
|
|
|
|
int dijkstra(int S) {
|
|
|
memset(st, 0, sizeof st);
|
|
|
memset(dis, 0x3f, sizeof dis);
|
|
|
dis[S] = 0;
|
|
|
priority_queue<PII, vector<PII>, greater<PII>> q;
|
|
|
q.push({0, S});
|
|
|
|
|
|
while (q.size()) {
|
|
|
PII t = q.top();
|
|
|
q.pop();
|
|
|
|
|
|
int u = t.second;
|
|
|
if (st[u]) continue;
|
|
|
st[u] = true;
|
|
|
|
|
|
for (int i = h[u]; ~i; i = ne[i]) {
|
|
|
int v = e[i];
|
|
|
if (dis[v] > dis[u] + w[i]) {
|
|
|
dis[v] = dis[u] + w[i];
|
|
|
q.push({dis[v], v});
|
|
|
}
|
|
|
}
|
|
|
}
|
|
|
int res = 0;
|
|
|
for (int i = 1; i <= n; i++) { // 遍历每只奶牛
|
|
|
int j = id[i]; // j号牧场
|
|
|
if (dis[j] == INF) return INF; // 如果j号牧场失联了,则无法获得结果
|
|
|
res += dis[j]; // 累加一个最小距离
|
|
|
}
|
|
|
return res; // 整体的最小距离
|
|
|
}
|
|
|
int main() {
|
|
|
memset(h, -1, sizeof h);
|
|
|
cin >> n >> p >> m; // 奶牛数,牧场数,牧场间道路数
|
|
|
for (int i = 1; i <= n; i++) cin >> id[i]; // 1 到 N 头奶牛所在的牧场号
|
|
|
|
|
|
while (m--) {
|
|
|
int a, b, c;
|
|
|
cin >> a >> b >> c;
|
|
|
add(a, b, c), add(b, a, c);
|
|
|
}
|
|
|
int ans = INF;
|
|
|
|
|
|
// 枚举每个牧场为出发点,计算它的最短距离和 中的最小值
|
|
|
for (int i = 1; i <= p; i++) ans = min(ans, dijkstra(i));
|
|
|
|
|
|
printf("%d\n", ans);
|
|
|
return 0;
|
|
|
}
|
|
|
```
|
|
|
|
|
|
#### [$AcWing$ $1126$. 最小花费](https://www.acwing.com/problem/content/1128/)
|
|
|
|
|
|
假设初始金钱为$N$,那么如果要在最后一个人的手里得到$100$元,可得公式:
|
|
|
$$\large N∗(1−z_1\%)∗(1−z_2\%)∗…∗(1−z_n\%)=100$$
|
|
|
|
|
|
$\Rightarrow$
|
|
|
$$\large N=\frac{100}{(1−z_1\%)∗(1−z_2\%)∗…∗(1−z_n\%)}$$
|
|
|
|
|
|
要想$N$尽可能小,那么就要让 **分母尽可能大** ,即求$(1−z_1\%)∗(1−z_2\%)∗…∗(1−z_n\%)$的最大值。
|
|
|
|
|
|
**输入样例**:
|
|
|
```cpp {.line-numbers}
|
|
|
3 3
|
|
|
1 2 1
|
|
|
2 3 2
|
|
|
1 3 3
|
|
|
1 3
|
|
|
```
|
|
|
|
|
|
**输出样例**:
|
|
|
```cpp {.line-numbers}
|
|
|
103.07153164
|
|
|
```
|
|
|
|
|
|
**$Code$**
|
|
|
```cpp {.line-numbers}
|
|
|
#include <bits/stdc++.h>
|
|
|
using namespace std;
|
|
|
|
|
|
const int N = 2010;
|
|
|
const int M = 2e5 + 10;
|
|
|
|
|
|
typedef pair<double, int> PDI; // 堆中数值是浮点数,注意区别
|
|
|
|
|
|
int n, m;
|
|
|
double dis[N];
|
|
|
bool st[N];
|
|
|
|
|
|
int h[N], e[M], ne[M], idx;
|
|
|
double w[M]; // 边权为浮点数,与一般的题目有区别
|
|
|
void add(int a, int b, double c) {
|
|
|
e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++;
|
|
|
}
|
|
|
int S, T;
|
|
|
void dijkstra() {
|
|
|
priority_queue<PDI> q; // 大顶堆
|
|
|
dis[S] = 1;
|
|
|
q.push({1, S});
|
|
|
|
|
|
while (q.size()) {
|
|
|
auto t = q.top();
|
|
|
q.pop();
|
|
|
int u = t.second;
|
|
|
if (st[u]) continue;
|
|
|
st[u] = true;
|
|
|
|
|
|
for (int i = h[u]; ~i; i = ne[i]) {
|
|
|
int v = e[i];
|
|
|
double a = 1 - w[i];
|
|
|
if (dis[v] < dis[u] * a) {
|
|
|
dis[v] = dis[u] * a;
|
|
|
q.push({dis[v], v});
|
|
|
}
|
|
|
}
|
|
|
}
|
|
|
}
|
|
|
|
|
|
int main() {
|
|
|
memset(h, -1, sizeof h);
|
|
|
cin >> n >> m;
|
|
|
|
|
|
while (m--) {
|
|
|
int a, b, c;
|
|
|
cin >> a >> b >> c;
|
|
|
double w = c * 0.01;
|
|
|
add(a, b, w), add(b, a, w);
|
|
|
}
|
|
|
|
|
|
cin >> S >> T;
|
|
|
|
|
|
dijkstra();
|
|
|
printf("%.8lf\n", 100 / dis[T]);
|
|
|
return 0;
|
|
|
}
|
|
|
```
|
|
|
|
|
|
#### [$AcWing$ $920$. 最优乘车](https://www.acwing.com/problem/content/922/)
|
|
|
|
|
|
**总结**:
|
|
|
① 建图是本题的关键!同一趟车,不管走几站,走多远,花多少钱,都算是同一趟车,边权都是$1$!
|
|
|
② 本题的输入也是一大特点,每趟车不知道具体有几站,只知道换行算结束,需要学习读入办法。
|
|
|
|
|
|
```cpp {.line-numbers}
|
|
|
#include <bits/stdc++.h>
|
|
|
|
|
|
using namespace std;
|
|
|
const int INF = 0x3f3f3f3f;
|
|
|
typedef pair<int, int> PII;
|
|
|
|
|
|
const int N = 1e5 + 10, M = N << 1;
|
|
|
|
|
|
int n; // 总共有N个车站
|
|
|
int m; // 开通了M条单程巴士线路
|
|
|
int h[N], e[M], w[M], ne[M], idx;
|
|
|
int dis[N]; // 最小距离数组
|
|
|
bool st[N]; // 是否在队列中
|
|
|
|
|
|
int stop[N]; // 站点数组
|
|
|
|
|
|
void add(int a, int b, int c) {
|
|
|
e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++;
|
|
|
}
|
|
|
// 求1号点到n号点的最短路距离,如果从1号点无法走到n号点则返回-1
|
|
|
void dijkstra() {
|
|
|
memset(dis, 0x3f, sizeof dis); // 求最小设最大
|
|
|
dis[1] = 0; // 1到自己,乘车数0
|
|
|
priority_queue<PII, vector<PII>, greater<PII>> q; // 小顶堆
|
|
|
q.push({0, 1}); // 1号入队列
|
|
|
|
|
|
while (q.size()) {
|
|
|
auto t = q.top();
|
|
|
q.pop();
|
|
|
int u = t.second;
|
|
|
if (st[u]) continue;
|
|
|
st[u] = true;
|
|
|
for (int i = h[u]; ~i; i = ne[i]) {
|
|
|
int v = e[i];
|
|
|
if (dis[v] > dis[u] + w[i]) {
|
|
|
dis[v] = dis[u] + w[i];
|
|
|
q.push({dis[v], v});
|
|
|
}
|
|
|
}
|
|
|
}
|
|
|
}
|
|
|
|
|
|
int main() {
|
|
|
memset(h, -1, sizeof h); // 初始化邻接表
|
|
|
cin >> m >> n; // 总共有N个车站,开通了M条单程巴士线路
|
|
|
while (m--) { // m条边
|
|
|
// ① 先读入第一个数字
|
|
|
int cnt = 0; // cnt一定要清零
|
|
|
cin >> stop[++cnt];
|
|
|
char ch = getchar();
|
|
|
while (ch == ' ') {
|
|
|
// ② 读入其它数字
|
|
|
cin >> stop[++cnt]; // 还有就继续读
|
|
|
ch = getchar(); // 为下一次做准备
|
|
|
}
|
|
|
// 这个建图建的妙啊!
|
|
|
// 通过多条边,成功映射了问题,将一趟车问题转化为多个点之间边是1问题
|
|
|
for (int i = 1; i <= cnt; i++)
|
|
|
for (int j = i + 1; j <= cnt; j++)
|
|
|
add(stop[i], stop[j], 1);
|
|
|
}
|
|
|
|
|
|
dijkstra();
|
|
|
if (dis[n] == INF)
|
|
|
puts("NO");
|
|
|
else
|
|
|
printf("%d\n", dis[n] - 1);
|
|
|
return 0;
|
|
|
}
|
|
|
```
|
|
|
#### [$AcWing$ $903$. 昂贵的聘礼](https://www.acwing.com/problem/content/905/)
|
|
|
|
|
|
**建图方式**
|
|
|
|
|
|
假入我们想要$A$物品,而$A$物品的原价是$w_1$元,如果有$B$物品作为交换的话,只需要$c_1$元就可以得到$A$物品,那我们不就相当于$B$物品和$c_1$元可以得到$A$物品,也就是等价于$B$到$A$的路径为$c_1$吗?
|
|
|
|
|
|
那每个物品的原价我们又该怎么处理呢?这里在建图上有一个特殊的技巧:建立一个 <font color='red' size=4><b>超级源点</b></font> $O$!
|
|
|
$O$到每个物品的距离就是物品的原价,而我们需要不断地交换来降低我们想要获得物品的花费,这就是一个最短路问题了。
|
|
|
|
|
|
* 每个点 $i$ 的价格 相当于 从点$0$到点 $i$ **连一条边**, **边权** 定义为点$i$的价格
|
|
|
* 每个点 $i$ 有多个可替代点: **从可替代点** 到点$i$ **连一条边**
|
|
|
* **结果**:顶点 $0$ 到 顶点 $1$ 的 **最短路**
|
|
|
|
|
|
<center><img src='https://img2022.cnblogs.com/blog/8562/202203/8562-20220315104736167-544730696.png'></center>
|
|
|
|
|
|
|
|
|
**等级限制**
|
|
|
|
|
|
* 酋长的女儿肯定是要娶到手的,所有的路径都会汇集在 $1$ 号点,也就是说 $1$ 号点是所有路径中都存在的点
|
|
|
|
|
|
* 假设 $1$号点等级为 $L_1$,则所有最短路的点都必须满足在 $[L_1-M,L_1+M]$ 范围内
|
|
|
|
|
|
* 如果只是将$[L_1-M,L_1+M]$ 这个区间作为最后的区间,会存在两个点的等级差超过了 $M$ 值,不符合题意,所以,这个区间还要继续缩小
|
|
|
|
|
|
依次枚举区间 $[L_1-M,L_1],[L_1-M+1,L_1+1],[L_1-M+2,L_1+2]...[L_1,L_1+M]$,这些小区间内的任意两个点的等级都不会超过 $M$ 值,并且同时保证了 $1$ 号点肯定在区间内。
|
|
|
|
|
|
因此,**依次求出每个小区间的最短路,最后再取最小值就是答案**
|
|
|
|
|
|
|
|
|
|
|
|
```cpp {.line-numbers}
|
|
|
#include <bits/stdc++.h>
|
|
|
using namespace std;
|
|
|
typedef pair<int, int> PII;
|
|
|
const int N = 110;
|
|
|
const int M = N * N; // 边数最多有n^2,这是顶天设置,此处与传统的题目不,一般的M= N<<1,此题目没有明确给出边数上限,直接认为N^2
|
|
|
const int INF = 0x3f3f3f3f;
|
|
|
|
|
|
int h[N], e[M], ne[M], w[M], idx;
|
|
|
void add(int a, int b, int c) {
|
|
|
e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx++;
|
|
|
}
|
|
|
|
|
|
int dis[N]; // 单源最短路径
|
|
|
bool st[N]; // 配合Dijkstra用的是否出队过
|
|
|
|
|
|
int L[N]; // 每个节点的等级
|
|
|
int n, m; // n个物品,m表示等级差距限制
|
|
|
|
|
|
int dijkstra(int l, int r) {
|
|
|
memset(dis, 0x3f, sizeof dis);
|
|
|
memset(st, 0, sizeof st);
|
|
|
priority_queue<PII, vector<PII>, greater<PII>> q;
|
|
|
// 距离,节点号
|
|
|
q.push({0, 0}); // 超级源点
|
|
|
dis[0] = 0;
|
|
|
|
|
|
while (q.size()) {
|
|
|
auto t = q.top();
|
|
|
q.pop();
|
|
|
int u = t.second;
|
|
|
if (st[u]) continue;
|
|
|
st[u] = true;
|
|
|
|
|
|
for (int i = h[u]; ~i; i = ne[i]) {
|
|
|
int v = e[i];
|
|
|
// 枚举边时,只处理等级在指定范围内
|
|
|
if (L[v] < l || L[v] > r) continue;
|
|
|
|
|
|
if (dis[v] > dis[u] + w[i]) {
|
|
|
dis[v] = dis[u] + w[i];
|
|
|
q.push({dis[v], v});
|
|
|
}
|
|
|
}
|
|
|
}
|
|
|
return dis[1];
|
|
|
}
|
|
|
|
|
|
int main() {
|
|
|
memset(h, -1, sizeof h); // 初始化邻接表
|
|
|
cin >> m >> n; // m:表示地位等级差距限制,n:物品的总数
|
|
|
|
|
|
for (int i = 1; i <= n; i++) { // 枚举每个节点
|
|
|
int p, l, cnt; // 价格 等级 替代品数目
|
|
|
cin >> p >> L[i] >> cnt;
|
|
|
|
|
|
add(0, i, p); // 虚拟源点0, 0获取i号物品,需要p这么多的金币
|
|
|
|
|
|
while (cnt--) { // 读入物品i的替代品
|
|
|
int u, v; // 替代品的编号 和 优惠价格
|
|
|
cin >> u >> v; // u:替代品编号,v:收到替代品后的收费价格
|
|
|
add(u, i, v); // 从替代品向可替代品引一条长度为v的边
|
|
|
}
|
|
|
}
|
|
|
// 预求最小,先设最大
|
|
|
int res = INF;
|
|
|
// 枚举区间范围进行多次求最小路径
|
|
|
for (int i = L[1] - m; i <= L[1]; i++)
|
|
|
res = min(res, dijkstra(i, i + m));
|
|
|
// 输出结果
|
|
|
cout << res << endl;
|
|
|
return 0;
|
|
|
}
|
|
|
```
|
|
|
|
|
|
$TODO$
|
|
|
#### [$P2176$ $RoadBlock$ $S$](https://www.luogu.com.cn/problem/P2176)
|
|
|
```cpp {.line-numbers}
|
|
|
|
|
|
``` |