python/TangDou/Topic/HuanGenDp/1073.md

AcWing 1073. 树的中心

一、题目描述

给定一棵树，树中包含 n 个结点（编号1~n）和 n−1 条无向边，每条边都有一个权值。

请你在树中找到一个点，使得该点到树中其他结点的最远距离最近。

输入格式 第一行包含整数 n。

接下来 n−1 行，每行包含三个整数 a_i,b_i,c_i，表示点 a_i 和 b_i 之间存在一条权值为 c_i 的边。

输出格式 输出一个整数，表示所求点到树中其他结点的最远距离。

数据范围 1≤n≤10000, 1≤a_i,b_i≤n, 1≤c_i≤10^5

输入样例：

5 
2 1 1 
3 2 1 
4 3 1 
5 1 1

输出样例：

2

二、暴力大法

国际惯例上来就写暴力: 对每一个点都求得它的 最远距离, 答案=min(所有点的最远距离) 通过 7/11个数据然后TLE

#include <bits/stdc++.h>
using namespace std;

const int INF = 0x3f3f3f3f;
const int N = 10010, M = N << 1;
int n;
int ans;
int res = INF;

// 邻接表
int e[M], h[N], idx, w[M], ne[M];
void add(int a, int b, int c = 0) {
    e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx++;
}

void dfs(int u, int fa, int sum) {
    for (int i = h[u]; ~i; i = ne[i]) {
        int v = e[i];
        if (v == fa) continue;
        dfs(v, u, sum + w[i]);
    }
    ans = max(ans, sum);
}

int main() {
    memset(h, -1, sizeof h);
    cin >> n;
    for (int i = 1; i < n; i++) {
        int a, b, c;
        cin >> a >> b >> c;
        add(a, b, c), add(b, a, c);
    }
    // 暴力换根
    for (int i = 1; i <= n; i++) {
        ans = 0;
        dfs(i, 0, 0);
        res = min(res, ans);
    }
    printf("%d\n", res);
    return 0;
}

三、换根DP【模板，背诵】

注：与前一题类似，也是怕两重循环导致时间复杂度上升到O(N^2),不能遍历每两个节点，只能是遍历每个节点，尝试构建此节点的上下游信息，再用这些信息找出树的中心。

换根DP就是根据父亲的属性来更新他更新儿子的属性，相当于只需要考虑把顶点移到儿子对结果造成的影响。

同样，先来想一下如何暴力求解该问题：先 枚举 目标节点，然后求解该节点到其他节点的 最远距离

时间复杂度为 O(n^2)，对于本题的 数据规模，十分极限，经测试只能过 7/11

考虑如何优化求解该问题的方法

思考一下：在确定树的 拓扑结构 后单独求一个节点的 最远距离 时，会在该树上去比较哪些 路径 呢？

1. 从当前节点往下，直到子树中某个节点的最长路径
2. 从当前节点往上走到其父节点，再从其父节点出发且不回到该节点的最长路径

此处就要引入 换根DP 的思想了

换根DP 一般分为三个步骤：

1. 指定任意一个根节点
2. 一次dfs遍历，统计出当前子树内的节点对当前节点的贡献
3. 一次dfs遍历，统计出当前节点的父节点对当前节点的贡献，然后合并统计答案

那么我们就要先 dfs 一遍，预处理出当前子树对于根的 最大贡献(距离) 和 次大贡献（距离）

处理 次大贡献（距离） 的原因是：

如果 当前节点 是其 父节点子树 的 最大路径 上的点，则 父节点子树 的 最大贡献 不能算作对该节点的贡献

因为我们的路径是 简单路径，不能 走回头路

然后我们再 dfs 一遍，求解出每个节点的父节点对他的贡献（即每个节点往上能到的最远路径)

两者比较，取一个 max 即可

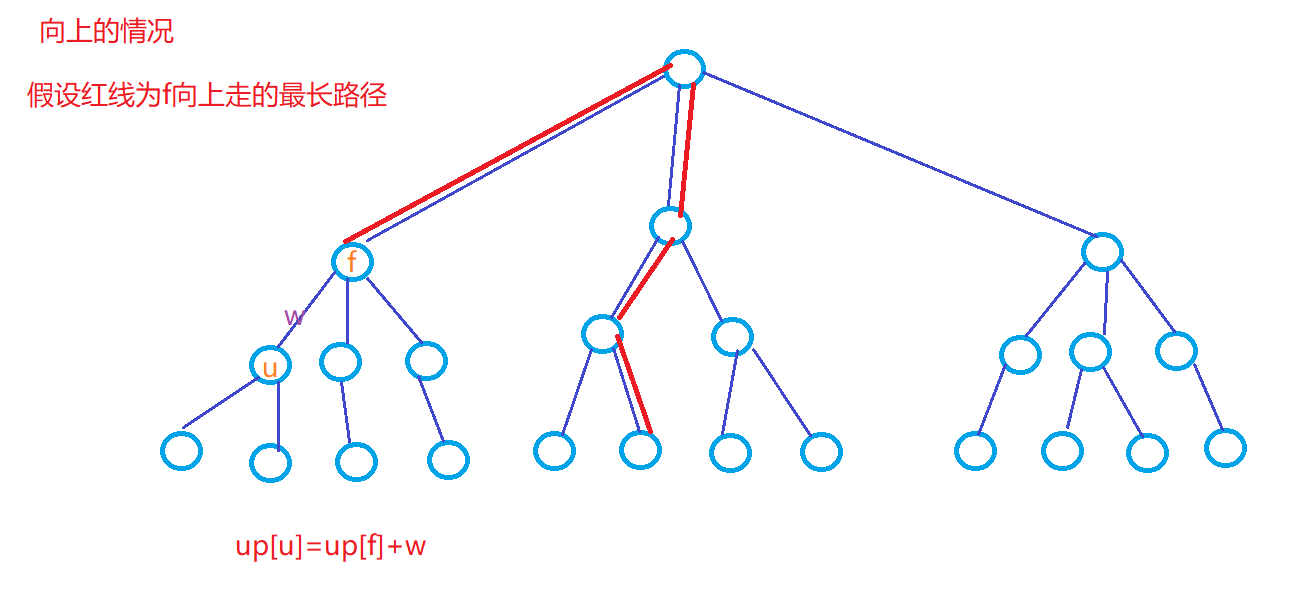
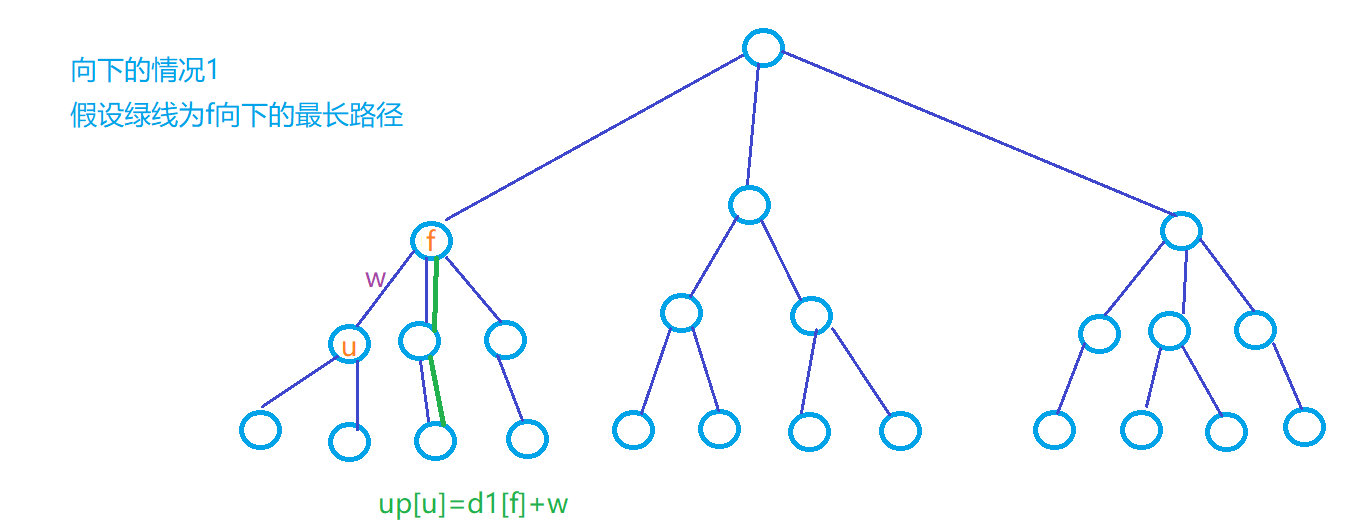
我们用 mx1[u],mx2[u],up[u],id[u]分别存一下需要的信息，这些数据存的是： mx1[u]：存下u节点向下走的最长路径的长度 mx2[u]：存下u节点向下走的第二长的路径的长度 id[u]：存下u节点向下走的最长路径是从哪一个节点下去的 up[u]：存下u节点向上走的最长路径的长度

图解

实现代码

#include <bits/stdc++.h>
using namespace std;

const int N = 10010, M = N << 1;
const int INF = 0x3f3f3f3f;

int n;      // n个节点
int mx1[N]; // mx1[u]：u节点向下走的最长路径的长度
int mx2[N]; // mx2[u]：u节点向下走的次长路径的长度
int id[N];  // id[u]：u节点向下走的最长路径是从哪一个节点下去的
int up[N];  // up[u]：u节点向上走的最长路径的长度

// 邻接表
int e[M], h[N], idx, w[M], ne[M];
void add(int a, int b, int c = 0) {
    e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx++;
}

// 功能:以u为根，向叶子进行递归，利用子节点返回的最长信息，更新自己的最长和次长,并记录最长是从哪个节点来的
void dfs1(int u, int fa) {
    for (int i = h[u]; ~i; i = ne[i]) {
        int v = e[i];
        if (v == fa) continue;

        // 递归完才能有数据
        dfs1(v, u);
        int x = mx1[v] + w[i]; // u问到：儿子v可以带我走多远？
        if (mx1[u] < x) {      // 更新最长
            mx2[u] = mx1[u];   // ① 更新次长
            mx1[u] = x;        // ② 更新最长
            id[u] = v;         // ③ 记录最长来源
        } else if (mx2[u] < x) // 更新次长
            mx2[u] = x;
    }
}

// 功能：完成向上的信息填充
void dfs2(int u, int fa) {
    for (int i = h[u]; ~i; i = ne[i]) {
        int v = e[i];
        if (v == fa) continue;
        // 二者取其一
        if (id[u] == v)
            up[v] = max(mx2[u], up[u]) + w[i];
        else
            up[v] = max(mx1[u], up[u]) + w[i];
        // 递归
        dfs2(v, u);
    }
}

int main() {
    memset(h, -1, sizeof h);
    cin >> n;
    for (int i = 1; i < n; i++) {
        int a, b, c;
        cin >> a >> b >> c;
        add(a, b, c), add(b, a, c);
    }
    dfs1(1, 0); // 选择任意一个节点进行dfs,用儿子更新父亲的统计信息
    dfs2(1, 0); // 向上

    int res = INF;
    for (int i = 1; i <= n; i++) res = min(res, max(mx1[i], up[i]));
    printf("%d\n", res);

    return 0;
}