python/TangDou/Topic/容斥原理.md

容斥原理专题

一、模板题

AcWing 890. 能被整除的数

题意：给定一个质数序列，求1 \sim n中被质数序列中 至少一个整除 的整数有多少个。

解题思路 ① 至少被一个质数整除,正向思考就是:被1个除，被2个除，被3个除,..., 用测试用例举栗子：

10 2
2 3

表示n=10,质数序列为2 3,那么: 2能够被质数2整除 3能够被质数3整除 4能够被质数2整除 6能够被质数2,3整除 8能够被质数2整除 9能够被质数3整除 10能够被质数2整除

看了一下，感觉6有点特殊:别人都是被1个质数整除，只有它是被2个质数整除。 为什么呢？思考一下，原来是因为6=2\times 3,也就是6中同时有2和3两个质数因子，而其它的只有一个质数因子。

② 这么一个个的检查怕是不行，因为n,p_i<=10^9,这样遍历一次就TLE了，需要有一个快速些的算法。那有什么样的办法能够做到快点计算出一个区间内有多少个2,3,x...的倍数呢？这是一个小学数学问题，遇到事决，小学数学：

[1 \sim n]中被p整除的数个数= ⌊\frac{n}{p}⌋

注：这里可不是说质数，比如我们想计算10以内6的倍数,就是10/6=1,这个1需要减去~

有了这个办法，就可以快速计算了，但问题马上又来了：

因为6即能被2整除，也能被3整除，这样就会被计算2次!

⌊\frac{10}{2}⌋+⌊\frac{10}{3}⌋=5+3=8 而我们用纸笔一个个查出来的是7个，这样算的结果多出来1个，很显然，就是因为6被记录了两次，需要把记录两次的扣除掉一次,噢，这是容斥原理啊！如果某个数是三个质因子的倍数，那么还需要加上它,....

② 容斥原理算法步骤 质因子站好排后，使用二进制数位枚举来每个质因子是不是选择了，这样可以穷举所有的可能 ，需要注意的是二进制需要从1开始枚举，一直到2^m-1。

注：m为质因子的个数，2^m-1就是共m位，每个位置上都是数字1,表示全部选中。根据选择了因数数量的奇偶性，决定它的加或减。 举栗子： 2^2-1=4-1=3=(11)_2 2^3-1=8-1=7=(111)_2 2^4-1=16-1=7=(1111)_2 2^5-1=32-1=7=(11111)_2 注意：在枚举过程中，如果出现2\times 3 \times 7 \times 11=462，如果n=100,那么这组解无效，因为超过了极限值嘛，所以此时组合选择需要放弃掉。

Code

#include <bits/stdc++.h>

using namespace std;
#define int long long
#define endl "\n"

int n, m;      // n:质数个数，m:1~m的数字中有多少个可以被质数序列中至少一个整数整除。
               // 注意：代码里的n,m与模板题目中的含义相反！一定要注意!!!!!!!!!!!!
vector<int> p; // 质数数组

signed main() {
    cin >> m >> n; // 与m互质,n个质数！

    // 读入n个质数,为了使用vector<int>，读入时确实不太方便
    for (int i = 0; i < n; i++) {
        int x;
        cin >> x;
        p.push_back(x);
    }

    // ① 枚举从1到 2^n-1,每个数字，代表一种状态，每个状态代表一种质数的挑选办法
    // 当然，这些整数值的乘积可能大于n,大于的没用，只要小于等于n的
    int s = 0;
    for (int i = 1; i < 1 << p.size(); i++) {
        int t = 1, cnt = 0; // 累乘积，质因子个数
        // ② 在对应的整数值确定后，枚举此数值的每一个数位
        for (int j = 0; j < p.size(); j++)
            if (i >> j & 1) {       // ③判断当前数位是不是1,是1表示当前数位选中
                if (t * p[j] > m) { // 乘积不能超过最大值m，控制在[1~m]范围内
                    t = 0;          // s=0代表本次挑选的组合失败，无效
                    break;          // 由于i是由小到大遍历的，前面的都无效了，后面的肯定更大，更无效，不用继续了
                }
                cnt++;     // 选择的质因子个数
                t *= p[j]; // 累乘积
            }
        if (t) {            // 超过范围的，s=0,所以，现在代表只讨论在范围内的
            if (cnt & 1)    // 质数因子数量，奇数加
                s += m / t; // 引理内容，代表m里面有多少个这个数字s的倍数
            else            // 偶数减
                s -= m / t;
        }
    }
    cout << s << endl;
}

二、题单

HDU4135 Co-prime

题意: 给三个数a、b 和 m，求区间[a,b]中与m互质的数的个数。 1 <= a <= b <= 10^{15}，1 <=m <= 10^9。

解析：

这道题与模板题不太一样，加入了一些变化，分析一下：

先从这句话下手：与m互质 答：就是把m分别质因数后，形成一个质数序列p_1,p_2,...,p_x,然后我们可以根据模板题， ① 求出来1 \sim a-1之间的所有数被p_1,p_2,...,p_x中的至少一个数整除的整数有多少个。 ② 求出来1 \sim b之间的所有数被p_1,p_2,...,p_x中的至少一个数整除的整数有多少个。

二者之差(类似前缀和)就是这个区间[a,b]之间与m不互质的数的个数 互质的个数等于总数减去不互质的个数就行啦~

Code

#include <bits/stdc++.h>
using namespace std;
#define int long long
#define endl "\n"

vector<int> p;          // 质数数组
int cal(int n, int m) { // 返回1-m中与n互素的数的个数
    p.clear();          // 多组测试数据,清空
    // 分解质因数
    for (int i = 2; i * i <= n; i++) { // 对n分解质因数
        if (n % i == 0) {
            p.push_back(i);
            while (n % i == 0) n /= i;
        }
    }
    if (n > 1) p.push_back(n); // 最后一个大因子，也加入

    int s = 0; // 1到m中与n不互素的数的个数

    // 枚举子集，不能有空集，所以从1开始
    for (int i = 1; i < 1 << p.size(); i++) { // 从1枚举到(2^素因子个数)
        int cnt = 0;
        int t = 1;
        for (int j = 0; j < p.size(); j++) { // 枚举每个素因子
            if (i & (1 << j)) {              // 有第i个因子
                cnt++;                       // 计数
                t *= p[j];                   // 乘上这个质因子
            }
        }
        // 容斥原理
        if (cnt & 1) // 选取个数为奇数，加
            s += m / t;
        else // 选取个数为偶数，减
            s -= m / t;
    }
    return m - s; // 返回1-m中与n互素的数的个数
}

signed main() {
    int T, ca = 0;
    cin >> T;

    while (T--) {
        int m, a, b;
        cin >> a >> b >> m; // 求区间[a,b]中与m互素的数字个数
        // 计算[1,a-1]之间与m互素的个数
        // 计算[1,  b]之间与m互素的个数
        int ans = cal(m, b) - cal(m, a - 1);
        printf("Case #%d: %lld\n", ++ca, ans);
    }
}

HDU2841 Visible Trees

题意

给一个n*m的矩阵，左下角为(1,1)，右上角为(n,m)，问农民在(0,0)点可以看到多少个点。

分析

解题思路

如果(0,0) \rightarrow (x,y)和(0,0)\rightarrow(x′,y′)两个向量共线，即(0,0),(x,y),(x′,y′)三点共线，那后面的那个点(x′,y′)就被挡住看不到了。

如果三点共线，那么向量(x′,y′)一定可以表示成(x'=kx,y'=ky)(其中k \in Z^+且k>1,kx<=n,ky<=m)，因此对于一个数对(x，y),如果它们存在公因数，那么一定可以化简成最简，即互质的形式，那么这个互质的数对构成的向量应该是和原向量共线的，因此我们 只能看到最前面那个互质的数对构成的点,其它不互质的都会被它前面的某个互质的挡住。

因此题目转变成求区间[1,m],[1,n]之间互质数的对数

求解办法：

选取一个区间（为了优化选取小区间）比如说选取[1,n]，枚举n里面的数i，然后对于每个数i我们看它在[1,m]区间内能找到多少互质的数，把这些结果全部累加起来即可。也就是枚举一个小区间中的所有数，然后转化为： 求1\sim n中与m互素的数的个数

注：通常情况下，小的循环在外层，大的循环在内层会更有利于性能。这是因为内存访问模式对性能有重要影响，将内存中的数据按照连续的顺序访问会更高效。当小的循环在外层时，内存中的数据更有可能按照连续顺序被访问，这有助于提高缓存的命中率，从而提高性能。

Code

#include <bits/stdc++.h>
using namespace std;
#define int long long
#define endl "\n"
const int N = 1e6 + 10;

// 返回1-m中与n互素的数的个数
vector<int> p;
int cal(int n, int m) {
    p.clear();
    for (int i = 2; i * i <= n; i++) {
        if (n % i == 0) {
            p.push_back(i);
            while (n % i == 0) n /= i;
        }
    }
    if (n > 1) p.push_back(n); // 求n的素因子

    int s = 0; // 1到m中与n不互素的数的个数

    // 枚举子集，不能有空集，所以从1开始
    for (int i = 1; i < 1 << p.size(); i++) { // 从1枚举到(2^素因子个数)
        int cnt = 0;
        int t = 1;
        for (int j = 0; j < p.size(); j++) { // 枚举每个素因子
            if (i & (1 << j)) {              // 有第i个因子
                cnt++;                       // 计数
                t *= p[j];                   // 乘上这个质因子
            }
        }
        // 容斥原理
        if (cnt & 1) // 选取个数为奇数，加
            s += m / t;
        else // 选取个数为偶数，减
            s -= m / t;
    }
    return m - s; // 返回1-m中与n互素的数的个数
}

signed main() {
    int T;
    cin >> T;
    while (T--) {
        int a, b;
        cin >> a >> b;
        int res = 0;
        // 从1~n(b现在就是n)之间，找到所有与m(m现在就是i)互质的数字个数
        for (int i = 1; i <= a; i++) res += cal(i, b);
        printf("%lld\n", res);
    }
}

HDU1695 HDU 1695 GCD（容斥原理）

题意 给了 a、b、c、d、k 五个数 求gcd(x,y)=k的 对数, 其中 a<=x<=b ,c<=y<=d 并且所有数据的a和c都是1。

分析

gcd(x,y)=k \rightarrow gcd(x/k，y/k)=1 (1<=x<=b/k, 1<=y<=d/k) 也就是求互质的对数 那么,我们可以去枚举x的范围去算y中与x互质的个数,但 为了避免重复的情况 比如1 3 和3 1算一对 那么我们就假定x<y 所以我们算的是 大于x,小于等于y,并且与x互质的个数

用容斥原理算出大于x小于等于y的数中是x的质因数的倍数的个数sum, 然后y-x-sum就是x与1 \sim d/k中互质的对数。

#include <bits/stdc++.h>
using namespace std;
#define int long long
#define endl "\n"

// 返回1-m中与n互素的数的个数
vector<int> p;
int cal(int n, int m) {
    p.clear();
    for (int i = 2; i * i <= n; i++) {
        if (n % i == 0) {
            p.push_back(i);
            while (n % i == 0) n /= i;
        }
    }
    if (n > 1) p.push_back(n); // 求n的素因子

    int s = 0; // 1到m中与n不互素的数的个数

    // 枚举子集，不能有空集，所以从1开始
    for (int i = 1; i < 1 << p.size(); i++) { // 从1枚举到(2^素因子个数)
        int cnt = 0;
        int t = 1;
        for (int j = 0; j < p.size(); j++) { // 枚举每个素因子
            if (i & (1 << j)) {              // 有第i个因子
                cnt++;                       // 计数
                t *= p[j];                   // 乘上这个质因子
            }
        }
        // 容斥原理
        if (cnt & 1) // 选取个数为奇数，加
            s += m / t;
        else // 选取个数为偶数，减
            s -= m / t;
    }
    return m - s; // 返回1-m中与n互素的数的个数
}

int T, ca;
signed main() {
    cin >> T;
    while (T--) {
        int a, b, c, d, k;
        cin >> a >> b >> c >> d >> k;
        // k=0时需要特判，因为我们想要 x'=x/k ,y'=y/k,不能随意除，需要判断
        if (k == 0) { // k=0时，表示gcd(x,y)=0
            /*
            如果两个数的最大公约数是0，这意味着这两个数中至少有一个数是0。
            因为最大公约数是两个数共有的最大因子，而0没有最大因子，所以0
            与任何数的最大公约数都是0。
            而a<=x<=b,c<=y<=d,a=c=1,所以，k=0是不可能存在gcd(x,y)=0的，应该返回0对
            */
            printf("Case %lld: 0\n", ++ca);
            continue;
        }
        b /= k, d /= k;
        // 因为 (1，3)与 (3,1)算1个，所以要限制x<y
        // a=c=1
        if (b > d) swap(d, b);
        int ans = 0;
        // d>b
        for (int i = 1; i <= d; i++) // 枚举大区间
            // c(n,m): 返回1-m中与n互素的数的个数
            // 拿大区间[1~d]中的每个数字i，去 [1~b]中找与其互质的数
            // 但是，这样做的话，会出现 [1,3],[3,1]这样的情况，为了防止这样的事情发生
            // 我们需要控制区间的范围，也就是小于等于i,同时，也要考虑i与b的大小关系，保证i<=b
            // 也就是 min(i,b)
            ans += cal(i, min(i, b));
        printf("Case %lld: %lld\n", ++ca, ans);
    }
}

AcWing 214. Devu和鲜花

思路脉络 ① 隔板法，每组内允许为0个，也就是隔板法扩展 ② 但每个分组中最高的数量有限制！ ③ 正难则反，先用隔板法扩展求一下每个小组可以为0的所有方案数 ④ 总的方案数减去每个盒子中不满足条件的并不是答案，因为可能减多了，联想到容斥原理。 ⑤ S_i代表每组中至少取出a_i+1朵花，那就先拿走这些，然后考虑m-(a_i+1)朵花中分成n组、并且每组数量可以为0的方案数，这是经典的隔板扩展法，然后再把拿走的a_i+1朵花拿回来到i组中，有原来的情况一致。 ⑥ 与上一题的区别在于：上一题必须保证有一个及以上的因子，也就是for (int i = 1;i < 1 << n; i++),本题可以一个都不选，即：for (int i = 0;i < 1 << n; i++)

#include <bits/stdc++.h>
using namespace std;
#define int long long
#define endl "\n"
const int N = 20, mod = 1e9 + 7;

int A[N];
int n, m;

// 快速幂
int qmi(int a, int k) {
    int res = 1;
    while (k) {
        if (k & 1) res = res * a % mod;
        a = a * a % mod;
        k >>= 1;
    }
    return res;
}

int C(int a, int b) {
    if (a < b) return 0;
    int up = 1, down = 1;
    for (int i = a; i > a - b; i--) up = i % mod * up % mod;
    for (int i = 1; i <= n - 1; i++) down = i * down % mod; //(n-1)! % mod
    down = qmi(down, mod - 2);                              // 费马小定理求逆元

    return up * down % mod; // 费马小定理
}

signed main() {
    cin >> n >> m;
    for (int i = 0; i < n; i++) cin >> A[i]; // 第i个盒子中有A[i]枝花,限制条件

    int res = 0;
    for (int i = 0; i < 1 << n; i++) { // 容斥原理的项数，0000 代表一个限制条件都没有， 0001代表第1个限制条件生效，0011,代码第1，2个限制条件生效
        int a = m + n - 1, b = n - 1;  // 上限是m+n-1,下限不一样
        int sign = 1;                  // 奇数个限制条件，需要减；偶数个限制条件，需要加。现在这种限制条件组合状态，是奇数个限制，还是偶数个限制？
        for (int j = 0; j < n; j++)    // 枚举状态的每一位
            if (i >> j & 1) {          // 如果此位是1
                sign *= -1;            // 符号位变号，从1变为-1，或者，从-1变为1; 这个用法挺牛X的，漂亮的实现了奇数次负号，偶数次正号的维护
                a -= A[j] + 1;         // 拼公式
            }
        res = (res + C(a, b) * sign) % mod;
    }
    cout << (res + mod) % mod << endl;
}

HDU3501 Calculation 2

等差数列

是指从第二项起，每一项与它的前一项的差等于同一个常数的一种数列，常用A、P表示，这个常数叫做等差数列的公差，公差常用字母d表示。例如：1，3，5，7，9，2n-1。通项公式为：a_n=a_1+(n-1)*d。首项a_1=1，公差d=2，前n项和公式为：

\large S_n=n*(a_1+a_n)/2  

注意：n \ \in Z^+

公式推导

\large S_n=a_1+a_2+a_3+...+a_n。

把上式倒过来得：\large S_n=a_n+a_{n-1}+a_2+a_1。

将以上两式相加得：\large 2S_n=(a_1+a_n)+(a_2+a_{n-1})+...+(a_n+a_1)。

由等差数列性质：若m+n=p+q则a_m+a_n=a_p+a_q得

\large 2S_n=n(a_1+a_n)

注：括号内其实不只是a_1+a_n满足只要任意满足下角标之和为n+1就可以两边除以2得s_n=n(a_1+a_n)/2 ①

题意 输入n,计算比n小的数中,和n不互质的数的和 \%1000000007

解题思路

求小于N\ (1 \sim N-1)的数字中与N 不互质 的数的 加法和。

与N不互质，就与N有相同因子,首先将N因式分解，找出所有的质因子。

对于累乘积因子2,有2,4,6,8,…… 对于累乘积因子3,有3,6,9,12,…… 对于累乘积因子6,有6,12,18,……

也就是需要加上2的那一坨，加上3的那一坨，再减去6的那一坨,... 而这些坨，都是等差数列，可以用 等差数列求和公式 求解。

Code

#include <bits/stdc++.h>
using namespace std;
#define int long long
#define endl "\n"
const int mod = 1000000007;

signed main() {
    int m;
    while (cin >> m && m) {
        if (m == 1) {
            cout << "0" << endl;
            // 边界需要特别注意！本题的左边界是1
            // 表示的含义是小于1，并且与1不互质的数的加法和，当然是0。
            // 在做题时，先想正常思路，然后再思考一下边界是不是用特判。
            continue;
        }

        int n = m; // 复制出来进行质因数分解

        // 分解质因数
        vector<int> p;
        for (int i = 2; i * i <= n; i++) {
            if (n % i == 0) {
                p.push_back(i);
                while (n % i == 0) n = n / i;
            }
        }
        if (n > 1) p.push_back(n);

        // 容斥原理
        int s = 0;
        for (int i = 1; i < (1 << p.size()); i++) {
            int cnt = 0;
            int t = 1;
            for (int j = 0; j < p.size(); j++) {
                if (i >> j & 1) {
                    cnt++;
                    t *= p[j];
                }
            }

            /* t:质因子的累乘积
               cnt:质因子的个数
               举栗子：
               枚举到的组合中只有数字2,那么2，4，6，8，10，....需要加上
               枚举到的组合中只有数字3,那么3，6，9，12，15，....需要加上
               枚举到的组合中中6.有数字2，3,那么6，12，18，....需要减去
            */
            int num = (m - 1) / t; // 题目要求：比m小的数字中，也就是[1~m-1]这些数字中有多少个数是t的倍数呢?是(m-1)/t个。
            /* 这些数字,首个是t,第二个是t*2,最后一个是t*num
               等差数列求和公式：(首项+末项)*项数/2
               模板题是计数，这里不是计数，而是计算这些数加在一起是多少，不能傻傻的一个个累加，而是采用了数学中的等差数列求和公式，
               否则聪明的高斯该生气了~
            */
            int tmp = (t + t * num) * num / 2;

            if (cnt & 1) // 奇数的加
                s += tmp;
            else // 偶数的减
                s -= tmp;
        }
        cout << s % mod << endl; // 取模输出
    }
}

HDU 1796 How many integers can you find

题意 给你一个整数N。和M个整数的集合{A_1、A_2、…、A_m}。集合内元素为 非负数 (包括零)，求小于N的

正整数(1\sim N-1)中，能被M个整数的集合中随意一个元素整除的正整数个数。

比如N = 12,M = {2，3}，在1\sim N-1中，能被2整除的数为{2,4,6,8,10}，能被3整除的数为{3,6,9}。则所求集合为{2，3，4。6，8，9，10}，共7个，则答案为7。

解题思路 就是求M个集合的并集。先看上边的样例。能被2整除的数集合S_1为{2,4,6,8,10}，能被3整除的数 集合S_2为{3,6,9}。而两者交集S_{12}为能被LCM(2，3) = 6整除的数为{6}。

则两者并集 S = S_1 + S_2 - S_{12}。

依据容斥定理得：若有M个数，则可求出1~N-1中能被不同组合的公倍数整除的个数。

1\sim N-1能被公倍数整除的个数为 (N-1) / LCM。然后依据奇数项加，偶数项减的原则得出答案个数。

Code

#include <bits/stdc++.h>

using namespace std;
#define int long long
#define endl "\n"

const int N = 15;
vector<int> p;

// 最小公倍数
int lcm(int a, int b) {
    return a * b / __gcd(a, b);
}

signed main() {
    int n, m;
    while (cin >> m >> n) { // n个数，求[1~m)中有多少个数能被整除集合中的数字整除
        m--;                // small than m 注意细节
        p.clear();          // 多组测试数据，注意清0

        for (int i = 0; i < n; i++) { // n个数字组成的序列
            int x;
            cin >> x;
            if (x) p.push_back(x); // 排除掉数字0,0不能做除数
        }

        int s = 0;
        for (int i = 1; i < (1 << p.size()); i++) {
            int cnt = 0;
            int t = 1;
            for (int j = 0; j < p.size(); j++) {
                if (i >> j & 1) {
                    cnt++;
                    t = lcm(t, p[j]); // 这里不是简单的相乘，而是求的最小公倍数
                }
            }
            if (cnt & 1)
                s += m / t;
            else
                s -= m / t;
        }
        cout << s << endl;
    }
}

HDU 2204 Eddy's爱好

题意

如果一个数能表示为M^k，那么这个数是好数，问你1 \sim n有几个好数。

引理

100以内是某个数的2次方的数有多少个？怎么计算的？

对于这个问题，我们可以针对100以内的每个数进行计算，看其是否是某个数的2次方。但是，如果我们只是想要知道100以内有多少个数是某个数的2次方，我们可以 先对100进行开方，然后向下取整，得到的结果就是100以内的2次方数的个数。在这种情况下，100的开方是10，向下取整后得到10，这意味着100以内有10个数是某个数的2次方。

100以内是某个数的2次方的数包括：0, 1, 4, 9, 16, 25, 36, 49, 64, 和 81。

思路

如果我们直接按这个计算，会发现有很多重复，比如有个数是2的次方，也有可能是4的次方，也有可能是6的次方，但是这些其实在2的次方中就已经计算了，而4，8是2的倍数，所以我们只需要 管素数次方 就行了。

那是不是这样就没有重复了？也不是，不同数之间有可能也有，就比如一个数是6的次方，他就被素数2次方和素数3次方同时给统计了，这个要 用到容斥，比如27^2=729和9^3=729会重复,是因为他们都能凑出指数6，也就是27^2=3^{3^2}=3^6,9^3=3^{2^3}=3^6所以我们需要减去指数6所得到的个数。

我们用n计算出指数为6的个数，729^{1/6}=pow(729,1.0/6)=1

答案就是先+指数为2的，再+指数为3的，最后减指数为6的

这就是容斥原理的经典套路了，加奇数个的，减偶数个的。

指数范围

Q1:最多多少个质数因子? 答： 因为2是最小的质数因子，它的60次方 = 2^{60}>10^{18},也就是说，即使是最小的质数,它的60次方都超过了题目数据上限，所以，指数最大为60足够所有情况使用，打表60以内的素数，然后容斥。

Q2:最多容斥多少个质数？ 答：2*3*5*7>60，我们挑选最小的4个质数因子，就会超过上限60!所以，最多只有三个质数因子,不会有4个及以上的质数因子个数。

Code

#include <bits/stdc++.h>
using namespace std;
#define int long long
#define endl "\n"
// 60以内的质数列表
int p[] = {2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59};

signed main() {
    int n;
    while (cin >> n) {
        int s = 1, t;                   // s=1表示最起码数字1符合要求
        for (int i = 0; i < 17; i++) {  // 三层循环，遍历质数数组p枚举第一个因子
            t = pow(n, 1.0 / p[i]) - 1; // 计算出指数=p[i]的数的个数,需要减去1，见下面的注释解释
            if (!t) break;              // 扣除完1^2后，没有了，那太白扯了
            /*
            int n = 10;
            cout << (int)pow(n, 1.0 / 2) << endl;
            输出3，理解一下：
            10以内，可以描述为x^2的有：1^2 2^2 3^2
            这样，就是说上面的算法，把数字1记录在内了。
            */
            s += t; // t个，但数字1不能考虑

            for (int j = i + 1; j < 17; j++) {       // 三层循环，枚举第二个因子,避让第一个因子
                t = pow(n, 1.0 / (p[i] * p[j])) - 1; // 计算出指数=p[i]*p[j]的数的个数
                if (!t) break;                       // 扣除完1^2后，没有了，那太白扯了
                s -= t;                              // 两个的要减

                for (int k = j + 1; k < 17; k++) {              // 三层循环，枚举第三个因子,避让第一、第二个因子
                    t = pow(n, 1.0 / (p[i] * p[j] * p[k])) - 1; // 计算出指数=p[i]*p[j]*p[k]的数的个数
                    if (!t) break;                              // 扣除完1^2后，没有了，那太白扯了
                    s += t;                                     // 三个的要加
                }
            }
        }
        cout << s << endl;
    }
}

HDU 4407 Sum

题意

给一个长度为n的序列，初始值为1 \sim n;

对序列有以下两种操作；

1.查询[x,y]内与p互素的数的和；

2.修改第x数为c;

共m,(1 \leq m \leq 1000)次操作。

解题思路

如果我们先忽略操作2带来的影响，可以通过求calc(y)-calc(x-1)这种类似于前缀的方法来得出答案,其中calc(y)的含义就是计算从1\sim y之间与p互质的数字和，办法当然就是用补集思想先算总和=sum(1 \sim y),然后再计算出与p不互质的数字有哪些，用总和减去不互质的数字和，就是互质的数字和。

本题的数据比较特殊，是[1\sim n]序列，是一个等差数列。 经验告诉我们，需要对p先分解质因数,由于我们一般喜欢用vector<int> p来保存质因数序列，所以我管原来的输入p改名为P,小p变量名留给质因数序列数组。

一眼就看出来本题需要容斥原理+二进制枚举组合

利用二进制法枚举每种可能的质数因子组合，举栗子：2,3,5

本次枚举的是数字3,即(11)_2,得到质数组合(2,3) 取乘积 2*3=6 此时 t=6,n/t = n/6:计算[1 \sim n]里面6这个因子的倍数有多少个,比如有3个

即：6,12,18 我们需要把这3个数字和加到一起，(6+12+18),就是(1+2+3)*6 即：n * (n + 1) / 2 * d;

能不能证明一下这个公式呢？

我们先看基础公式S_n=(a_1+a_n)*n/2 在本题中，a_1=d,a_n=a1+(n-1)*d 代入 S_n=(d+d+(n-1)*d)*n/2=d*(2+n-1)*n/2=(n+1)*n/2*d 证毕

Q:修改怎么办？

本来是一个1\sim n的序列，这题目挺坏啊，将第x位的值修改为c ,这样，本来依靠等差数列求和之类的东西就无法使用了！ 所以，办法就是 先写基本盘，再做修改盘 的补充

注: 为m范围只到1000，所以暴力不超时

步骤 ① 遍历每个查询范围内的修改，如果原值与P互质，则减掉该数值 ② 如果修改的新值与P互质，则加上该数值。

#include <bits/stdc++.h>
using namespace std;
#define int long long
#define endl "\n"
const int N = 400010;

unordered_map<int, int> mp; // 能用Hash表不用红黑树
vector<int> p;              // 将m拆分成的质数因子序列p

/*
等差数列求和=(首项+末项)*项数/2
本题中：首项=t,项数=n,公差=t
举栗子：3,6,9 是一个等差数列，公差=3
我们可以这样看(1,2,3)*3,也就是先计算(1,2,3)的和，再乘以3=(1+3)*3/2*3=18
*/
int get(int t, int n) {
    return n * (n + 1) / 2 * t;
}
// 容斥原理+等差数列加法和
// 求解[1,n]中与c互素的所有数字的和
// = [1,n]的数字总和 - [1,n]中所有与c存在公共因子的数的和
int calc(int n) {
    int sum = get(1, n); // [1,n]的数字总和
    int s = 0;
   
    for (int i = 1; i < (1 << p.size()); i++) {
        int cnt = 0, t = 1;
        for (int j = 0; j < p.size(); j++) {
            if (i >> j & 1) {
                cnt++;
                t *= p[j];
            }
        }
        if (cnt & 1)
            s += get(t, n / t);
        else
            s -= get(t, n / t);
    }
    return sum - s; // 总数，减去不互质的，等于，互质的数字加法和
}
signed main() {
#ifndef ONLINE_JUDGE
    freopen("HDU4407.in", "r", stdin);
#endif
    // 加快读入
    ios::sync_with_stdio(false), cin.tie(0);

    int T; // T组测试数据
    cin >> T;
    while (T--) {
        mp.clear(); // 注意此处，每次测试案例都要清零
        int n, m;
        cin >> n >> m; // 1~n ，共n 个长度的序列
        while (m--) {  // m个询问
            int choice;
            cin >> choice; // 操作
            int x, y, P;
            if (choice == 1) { // 查询[x,y]内与c互素的数的和
                cin >> x >> y >> P;

                p.clear(); /// 初始化
                // 分解质因数
                int t = P; // 复制出来
                for (int i = 2; i * i <= t; i++) {
                    if (t % i == 0) {
                        p.push_back(i);
                        while (t % i == 0) t = t / i;
                    }
                }
                if (t > 1) p.push_back(t);

                int sum = calc(y) - calc(x - 1); // 类似于前缀和求[x~y]区间内的等差数列加法和

                // 遍历已经录入的所有修改
                for (auto it = mp.begin(); it != mp.end(); it++) {
                    int a = it->first, b = it->second;
                    // 如果修改的不存本次查询的范围内，改了也不影响我，没用，不理
                    if (a > y || a < x) continue;
                    // 本来互素,结果被你改了，那就需要减掉这个数值
                    if (__gcd(a, P) == 1) sum -= a;
                    // 修改后互素的要加上新数值
                    if (__gcd(b, P) == 1) sum += b;
                }
                cout << sum << endl;
            } else {
                cin >> x >> P;
                mp[x] = P; // 修改序列内容
            }
        }
    }
}

UVA 11806 Cheerleaders

考查了组合数公式、补集思想、容斥原理思想（不拘泥于质数+二进制枚举噢~）

题意

给定n、m、k三个数，n代表行数，m代表列数，k代表人数。

n*m的表格，一共有k个人，要求：

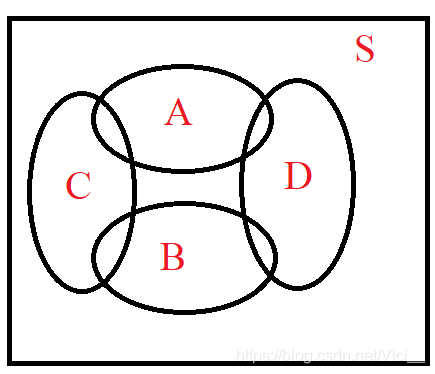
① 每个小格只能容纳一个人，所有人必须都在表格中。 ② 第一行、第一列、最后一行、最后一列必须站人。 ③ 若夹角处站人，则代表此行和列都已站人。

问：有多少种方法？

解题思路

利用容斥原理，设：

• S为总数。（n*m中选k个位置，即C_{n∗m}k）
• A为第一行没有站人。（少一行）
• B为最后一行没有站人。（少一行）
• C为第一列没有站人。（少一列）
• D为最后一列没有站人。（少一列）

文氏图如下：

采用 补集思想：所有可能的站法 - 所有不可能的站法 = 符合条件的所有站法。

我们要计算的就是，S减去ABCD覆盖部分。

容斥原理公式表示为：

ans=S−(A+B+C+D)+(AB+AC+AD+BC+BD+CD)−(ABC+ABD+ACD+BCD)+(ABCD)

记：

s_1=(A+B+C+D) s_2=(AB+AC+AD+BC+BD+CD) s_3=(ABC+ABD+ACD+BCD) s_4=(ABCD)

#include <bits/stdc++.h>
using namespace std;

const int mod = 1000007;
const int N = 410;
int C[N][N];
int n, m, k, ans;
/*
Sample Input
2
2 2 1
2 3 2
Sample Output
Case 1: 0
Case 2: 2
*/
int main() {
#ifndef ONLINE_JUDGE
    freopen("UVA11806.in", "r", stdin);
#endif
    // 预处理出组合数结果数组
    for (int i = 1; i < N; i++) {
        C[i][0] = C[i][i] = 1;
        for (int j = 1; j < i; j++)
            C[i][j] = (C[i - 1][j - 1] + C[i - 1][j]) % mod;
    }

    int T, cas = 1;
    int S, s1, s2, s3, s4;
    cin >> T;
    while (T--) {
        ans = 0;            // 多组测试数据，每次注意清零
        cin >> n >> m >> k; // n行,m列,k个人
        if (k == 0) {       // 一定要注意边界情况，比如0个人
            printf("Case %d: 0\n", cas++);
            continue;
        }

        S = C[n * m][k]; // n*m个格子中找出k个格子站人，就是所有方案数
        /*
        S为总数
        A为第一行没有站人
        B为最后一行没有站人
        C为第一列没有站人
        D为最后一列没有站人

        令：
        s1 =(A+B+C+D)
        s2=(AB+AC+AD+BC+BD+CD)
        s3=(ABC+ABD+ACD+BCD)
        s4=(ABCD)
        */

        // A:第一行没人，即C[(n-1)*m,k]
        // B:最后一行没人,即C[(n-1)*m,k]
        // C:第一列没人，即：C[n*(m-1),k]
        // D:最后一列没人，即：C[n*(m-1),k]
        s1 = 2 * (C[n * (m - 1)][k] + C[(n - 1) * m][k]) % mod;

        // AB:第一行，最后一行没有人，行少了2行，列不变，即C[(n-2)*m,k]
        // AC:第一行，第一列没有人，行少了1行，列少了一列，即C[(n-1)*(m-1),k]
        // AD:第一行，最后一列没有人，即C[(n-1)*(m-1),k]
        // BC:最后一行，第一列没有人，即C[(n-1)*(m-1),k]
        // BD:最后一行，最后一列没有人,即C[(n-1)*(m-1),k]
        // CD:第一列，最后一列没有人,即C[n*(m-2),k]
        // 中间4个是一样的：4*C[(n-1)*(m-1),k]
        s2 = (C[(n - 2) * m][k] + 4 * C[(n - 1) * (m - 1)][k] + C[n * (m - 2)][k]) % mod;

        // ABC:第一行、最后一行、第一列没有人，行少了2行，列少了1列，即C[(n-2)*(m-1),k]
        // ABD:第一行、最后一行、最后一列没有人，行少了2行，列少了1列，即C[(n-2)*(m-1),k]
        // ABC+ABD=2*C[(n-2)*(m-1),k]
        // ACD:第一行、第一列、最后一列没有人，行少了1行，列少了2列，即 C[(n-1)*(m-2),k]
        // BCD:最后一行、第一列、最后一列没有人，行少了1行，列少了2列，即 C[(n-1)*(m-2),k]
        // ACD+BCD=2*C[(n-1)*(m-2),k]
        s3 = 2 * (C[(n - 2) * (m - 1)][k] + C[(n - 1) * (m - 2)][k]) % mod;

        // 第一行，第一列，最后一行，最后一列都不能站，那么，剩下n-2行，m-2列，需要在(n-2)*(m-2)这么多的格子里找出k个格子
        s4 = C[(n - 2) * (m - 2)][k] % mod;

        ans = (S - s1 + s2 - s3 + s4) % mod; // 容斥原理
        ans = (ans + mod) % mod;             // 防止取余后出现负数
        printf("Case %d: %d\n", cas++, ans); // 输出答案
    }
    return 0;
}

ACM-ICPC 2018 沈阳赛区网络预赛G-Spare Tire

题意

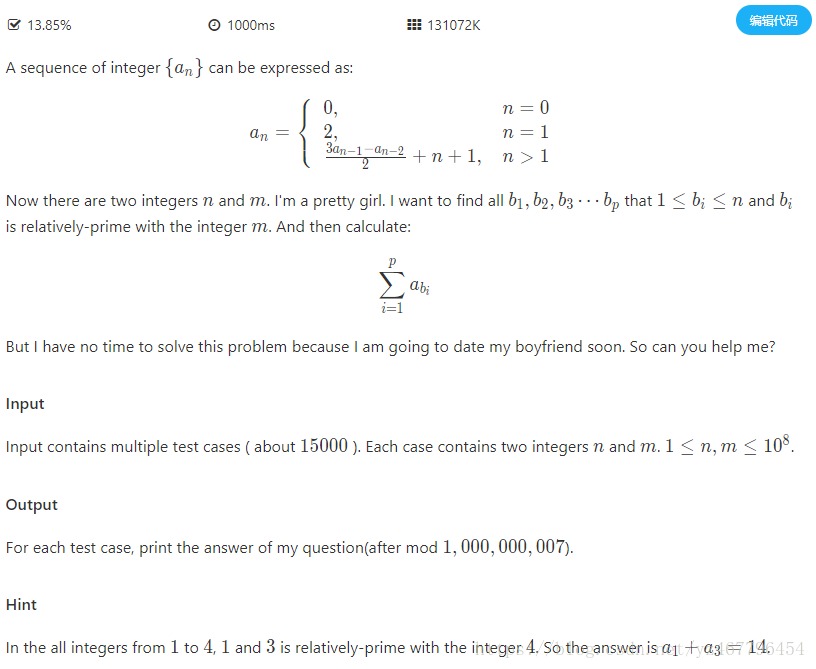
中文题意： 给出a的递推式，找出1到n中与m互质的数i，求a[i]和。

解题思路

结论：递推式 \large a_n = \frac{3a_{n-1} - a_{n-2}}{2} + n + 1 的通项公式为 a_n = n^2 + n。

可以使用数学归纳法来证明这个结论。

初值条件 当 n = 1 时，a_1 = 1^2 + 1 = 2,符合通项公式 a_n = n^2 + n。 当 n = 2 时，a_2 = 2^2 + 2 = 6,符合通项公式 a_n = n^2 + n。

归纳假设 假设对于所有的 n \leq m，递推式 a_n = \frac{3a_{n-1} - a_{n-2}}{2} + n + 1 的通项公式成立，即 a_n = n^2 + n。

归纳步骤 我们需要证明当 n = m+1 时，通项公式 a_n = n^2 + n 仍然成立。

根据递推式 a_n = \frac{3a_{n-1} - a_{n-2}}{2} + n + 1，我们有：

a_{m+1} = \frac{3a_m - a_{m-1}}{2} + m + 1+1

根据归纳假设，将 a_m 和 a_{m-1} 替换为 (m^2 + m) 和 ((m-1)^2 + (m-1))，得到：

a_{m+1} = \frac{3(m^2 + m) - ((m-1)^2 + (m-1))}{2} + m + 1+1 \rightarrow a_{m+1}=\frac{3m^2+3m-(m^2-2m+1)-m+1}{2}+m+1+1 \rightarrow a_{m+1}=\frac{3m^2+3m-m^2+2m-1-m+1}{2}+m+1+1 \rightarrow a_{m+1}=\frac{2m^2+4m}{2}+m+1+1 \rightarrow a_{m+1} = m^2 + 2m +m+1+ 1 \rightarrow a_{m+1} = m^2 + 2m +1+m+1 \rightarrow a_{m+1}= (m+1)^2 + (m+1)

因此，当 n = m+1 时，通项公式 a_n = n^2 + n 仍然成立。

综上所述，根据数学归纳法，递推式 a_n = \frac{3a_{n-1} - a_{n-2}}{2} + n + 1) 的通项公式为 a_n = n^2 + n

费了牛劲，终于求得a_n=n*n+n，那么前n项和S_n是多少呢？ 即S_n=a_1+a_2+a_3+...+a_n \rightarrow S_n=1^2+1+2^2+2+3^2+3+...+n^2+n 拆开来看: ① 1,2,3,...,n很显然是一个等差数列，

\large S_n'=(1+n)*n/2

② 1^2,2^2,3^2,...,n^2这个序列的求和公式是多少呢? 这是自然数平方求和数列,有公式：

\large S_n''=n*(n+1)(2*n+1)/6

这个东西是怎么来的呢?

推导过程 2³-1³=3×1²+3×1+1 3³-2³=3×2²+3×2+1 4³-3³=3×3²+3×2+1 ... ... (n+1)³-n³=3n²+3n+1

以上n个式子相加，得 (n+1)³-1=3(1²+2²+3²+...+n²)+3(1+2+3+...+n)+(1+1+1+...+1) 即(n+1)³-1=3(1²+2²+3²+...+n²)+3[n(n+1)/2]+n

令S''=1²+2²+3²+...+n² 3S''=(n+1)³-1-3n(n+1)/2-n 3S''=(n+1)³-3n(n+1)/2-(n+1) 3S''=(n+1)((n+1)^2-3n/2-1) S''=(n+1)(n^2+2n+1-3/2n-1)/3 S''=(n+1)(n^2+n/2)/3 S''=(n+1)(2n^2+n)/6 ∴S''=n(n+1)(2n+1)/6。

更多推导方法，看 《具体数学》学习笔记: 4.四种方法推导平方和公式

我们直接求与m互质的数较难，所以我们可以换个思路，求与 m不互质的数，那么与m不互质的数，是取m的素因子的乘积（因为根据唯一分解定理，任意个数都可看作的素数积），那么我们将m分解质因数，通过容斥定理，就可以得道与m不互质的数，总和sum减去这些数对应的a的和就是答案了。

代码细节

如果我们利用两个质数2,3组成了一个数t=6,那么在1\sim n范围内，一共几个6的倍数呢? 以前学习过，是 n/6=n/t 个， 即：t,2t,3t,…n/t*t

现在我们需要把i \in [t,2t,3t,…n/t*t]计算\sum a[i]

有公因子t,设i=t*j 我们观察每一项： a(i)=i^2+i=(t*j)^2+(t*j)=t^2*j^2+t*j 在平方和公式前面，要乘一个系数t的平方，同时在等差数列求和公式前面要乘一个系数t。

根据通项公式，可以以O(1)时间快速计算出结果:

\large s_x=t^2*s_x'+t*s_x''

Sample Input

4 4

Sample Output

14

Code

#include <bits/stdc++.h>
using namespace std;
#define int long long
#define endl "\n"

const int mod = 1e9 + 7; // 尽量这样定义mod ，减少非必要的麻烦

// 快速幂
int qmi(int a, int b) {
    int res = 1;
    a %= mod;
    while (b) {
        if (b & 1) res = res * a % mod;
        b >>= 1;
        a = a * a % mod;
    }
    return res;
}

vector<int> p; // 将m拆分成的质数因子序列p

signed main() {
#ifndef ONLINE_JUDGE
    freopen("SpareTire.in", "r", stdin);
#endif
    int n, m;

    int Six = qmi(6, mod - 2); // 因为需要用到 % 1e9+7 下6的逆元，用费马小定理+快速幂求逆元
    int Two = qmi(2, mod - 2); // 因为需要用到 % 1e9+7 下2的逆元，用费马小定理+快速幂求逆元

    while (cin >> n >> m) {
        // 所结果拆分为平方和公式，等差数列两部分
        // 注意：现在求的是整体值，还没有去掉不符合条件的数字
        int first = n * (n + 1) % mod * (2 * n + 1) % mod * Six % mod;
        int second = n * (n + 1) % mod * Two % mod;
        int res = (first + second) % mod;

        // 对m进行质因子分解
        int t = m; // 复制出来
        for (int i = 2; i * i <= t; i++) {
            if (t % i == 0) {
                p.push_back(i);
                while (t % i == 0) t = t / i;
            }
        }
        if (t > 1) p.push_back(t);

        /*
          容斥原理
          例如有3个因子，那么1<<3=8(1000二进制)
          然后i从1开始枚举直到7(111二进制），i中二进制的位置1表式取这个位置的因子
          例如i=3(11二进制) 表示取前两个因子，i=5（101）表示取第1个和第3个的因子
        */
        int s = 0;
        for (int i = 1; i < (1 << p.size()); i++) {
            int cnt = 0, t = 1;
            for (int j = 0; j < p.size(); j++)
                if ((i >> j) & 1) {
                    cnt++;
                    t *= p[j];
                }

            // 比如找到了s=6=2*3，需要知道s是奇数个，还是偶数个因子
            // n/s:范围内6的倍数有多少个
            int k = n / t;
            int x = k * (k + 1) % mod * (2 * k + 1) % mod * Six % mod;
            x = x * t % mod * t % mod; // 乘上t^2
            // 还需要累加等差数列部分
            // 首项是t,项数是k,末项 t*k
            x = (x + k * (t + t * k) % mod * Two % mod) % mod;

            if (cnt & 1)
                s = (s + x) % mod;
            else
                s = (s - x + mod) % mod;
        }
        // 输出
        cout << (res - s + mod) % mod << endl;
    }
}

AcWing 215. 破译密码