python/TangDou/Topic/卡特兰数专题.md

卡特兰数专题（Catalan）

一、什么是卡特兰数？

明安图数，又称卡塔兰数，英文名Catalan number，是组合数学中一个常出现于各种计数问题中的数列。以中国蒙古族数学家明安图 (1692-1763)和比利时的数学家欧仁·查理·卡塔兰 (1814–1894)的名字来命名，其前几项为(从第零项开始) : 1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862,16796, 58786 …

知乎 卡特兰数四连击

https://zhuanlan.zhihu.com/p/31317307 https://zhuanlan.zhihu.com/p/31526354 https://zhuanlan.zhihu.com/p/31585260 https://zhuanlan.zhihu.com/p/31050581

嘉持老师的优秀教学视频

卡特兰数的几何意义

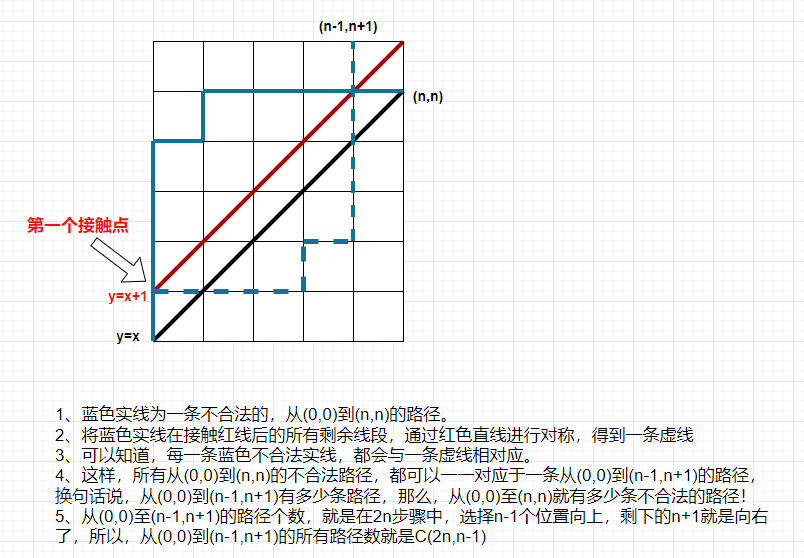
简单来说，卡特兰数就是一个有规律的数列，在坐标图中可以表示为：从原点(0,0)出发，每次向x轴或者y轴正方向移动1个单位，直到到达(n,n)点，且在移动过程中不越过第一象限平分线的移动方案总数。

卡特兰数公式推导

我们暂且先不考虑移动过程中不越过第一象限平分线这个约束条件，那么从(0,0)点到(n,n)点的过程中，我们总共需要向右移动n步，向上移动n步，一共2n步。我们可以理解为在2n步里面选出n步来向上移动，那么剩下的n步就是向右移动的步数，那么方案总数就是\LARGE \displaystyle C_{2n}^{n}

现在，我们来看看如何解决不越过第一象限平分线这个问题。仔细想想，不越过第一象限平分线也就等价于不触碰到y = x + 1这条直线。而我们如果把触碰到了直线y = x + 1的路线的第一个与y = x + 1的触碰点之后的路线关于直线y = x + 1对称，并画出对称后的路线

黄海解读

我们会发现触碰到了直线y = x + 1的路径的终点都变成了点(n-1,n+1)。也就是说，从(0,0)点到(n,n)点的路线当中触碰了直线y = x + 1的路线条数与从(0,0)点到(n-1,n+1)点的路线条数的数量是相等的。于是从(0,0)点到(n,n)点的非法路径条数为\LARGE \displaystyle C_{2n}^{n-1} 。

综上所述，从(0,0)点到(n,n)点满足条件的路径数为

卡特兰数通项公式I

\huge f(n)=C_{2n}^{n}-C_{2n}^{n-1}

---

通过化简，公式可以简化为：

\large Catalan_n= C_{2n}^{n}-C_{2n}^{n-1}=\frac{(2n)!}{n! \times n!}-\frac{(2n)!}{(n+1)!\times (n-1)!} \\ =\frac{(2n)!\times (n+1)}{n!\times (n+1)!}-\frac{(2n)!\times n}{n! \times (n+1)!} \\ =\frac{(2n)!\times (n+1)-(2n)!\times n}{n!\times (n+1)!} \\ =\frac{(2n)!}{n!\times (n+1)!}=\frac{1}{n+1}\times \frac{(2n)!}{n!\times n!}  =\frac{C_{2n}^n}{n+1}

卡特兰数通项公式II

\huge \displaystyle f(n)=\frac{C_{2n}^n}{n+1}

---

除了这个通项公式之外，卡特兰数还有一个由该通项公式推导而来的递推公式：

$\large \displaystyle Catalan_{n+1}= \frac{1}{n+2}C_{2n+2}^{n+1} \ =\frac{1}{n+2}\times \frac{(2n+2)!}{(n+1)!\times (n+1)!} \ =\frac{1}{n+2}\times \frac{(2n)!\times (2n+1) \times (2n+2)}{n! \times n!\times (n+1)^2} \ =\frac{1}{n+2}\times \frac{(2n+1)\times(2n+2)}{n+1} \times \frac{1}{n+1} \times \frac{(2n)!}{n!\times n!} \ =\frac{2(2n+1)}{n+2}\times \frac{1}{n+1}\times C_{2n}^n \ =\frac{4n+2}{n+2}Catalan_n $

初始值：f[0] = f[1] = 1

卡特兰数公式III(递推)

\huge f(n)=\frac{4n-2}{n+1}f(n-1)

卡特兰数公式IV(取模常用)

\huge f(n)=\frac{(2n)!}{(n+1)! \times n!}

卡特兰数公式V(递推)

一般不用来实现，用来推规律

\huge \displaystyle f(n)=\sum_{i=0}^{n-1}f(i)f(n-i-1)

证明：在n对括号的排列中，假设最后一个括号和第i个左括号匹配。则在第i个左括号之前，一定已经匹配上了(i-1)对左括号。如下图，因此，此种情况的数量为f(i-1)*f(n-i)。(1<=i<=n)最后一个右括号可以1\sim n个左括号匹配共n种情况。

因此，对i从1到n的情况求和得到\large \displaystyle f(n)=\sum_{i=0}^{n-1}f(i)f(n-i-1)，即可得到递推公式。

二、常见考点

1、 进出栈问题

设栈S的初始状态为空，元素a,b,c,d,e依次入栈，以下出栈序列有多少种可能性？注意：这个序列顺序是定的.

重点：归纳法思考，由大及小。

我们这样去想，假设最终的出栈序列可能性用f(n)表示，其中n就是元素的个数。

假设第k个数是最后出栈的数，那么:

• 比它小的前k-1个数，肯定已经完成了入栈，出栈操作。因为从逻辑顺序上来讲，它们无法压到k下面去吧。
• 比它大的后n-k个数，肯定已经完成了入栈，出栈操作。它们倒是可以压到k下面去，但假设k是最后一个出栈的，它们不能破坏掉假设，也必须提出出栈。

现在，k将原来的问题，划分为两个子问题f(n-k)和f(k-1),根据乘法原理，结果就是f(n-k)*f(k-1)。

k的取值范围是1 \leq k \leq n,再根据加法原理：

\large f(n)=\sum_{k=1}^{n}f(n-k)\times f(k-1)

展开写就是：\large f(n)=f(0) \times f(n-1) + f(1) \times f(n-2) + ... +f(n-1)\times f(0)

代码实现：

f[0] = 1;
for (int i = 1; i <= 12; i++) {
    int fi = 0;
    for (int j = 0; j <= i - 1; j++) fi += f[j] * f[i - j - 1];
    cout << fi << " ";
}

P1044 [NOIP2003 普及组] 栈

#include <bits/stdc++.h>

using namespace std;
typedef long long LL;
const int N = 20;
int f[N];
int main() {
    int n;
    cin >> n;
    f[0] = 1;
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= i; j++)
            f[i] += f[j - 1] * f[i - j];
    cout << f[n] << endl;
    return 0;
}

2、排队问题

变种（排队问题）：出栈入栈问题有许多的变种，比如n个人拿5元、n个人拿10元买物品，物品5元，老板没零钱。问有几种排队方式。熟悉栈的同学很容易就能把这个问题转换为栈。值得注意的是，由于每个拿5元的人排队的次序不是固定的，所以最后求得的答案要n!。拿10元的人同理，所以还要n!。所以这种变种的最后答案为h(n)*n!。 P1754 球迷购票问题

#include <bits/stdc++.h>

using namespace std;
typedef long long LL;
const int N = 30;
LL f[N];
int main() {
    int n;
    cin >> n;
    f[0] = 1;
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= i; j++)
            f[i] += f[j - 1] * f[i - j];
    cout << f[n] << endl;
    return 0;
}

3、 二叉树构成问题

有n个结点，问总共能构成几种不同的二叉树。

我们可以假设，如果采用中序遍历的话，根结点第k个被访问到，则根结点的左子树有k-1个点、根结点的右指数有n-k个点。k的取值范围为1到n。讲到这里就很明显看得出是卡特兰数了。

AcWing 1645. 不同的二叉搜索树 没有超过long long的存储范围的话，可以使用递推;

#include <bits/stdc++.h>

using namespace std;
typedef long long LL;
const int N = 1010, MOD = 1e9 + 7;

int n;
int f[N];

int main() {
    cin >> n;

    f[0] = 1;
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= i; j++)
            f[i] = (f[i] + (LL)f[j - 1] * f[i - j]) % MOD;

    cout << f[n] << endl;
    return 0;
}

AcWing 1317. 树屋阶梯 模拟，按照公式（1）进行模拟，需要使用高精度 黄海的题解

AcWing 1257. 二叉树计数

#include <bits/stdc++.h>
using namespace std;

const int N = 10010; // 5000*2+10
int primes[N], cnt;
bool st[N];
int a[N], b[N];

void get_primes(int n) {
    for (int i = 2; i <= n; i++) {
        if (!st[i]) primes[cnt++] = i;
        for (int j = 0; primes[j] * i <= n; j++) {
            st[i * primes[j]] = true;
            if (i % primes[j] == 0) break;
        }
    }
}

int get(int n, int p) { // n!中p的次数
    int s = 0;
    while (n) n /= p, s += n;
    return s;
}

void mul(int a[], int b, int &len) {
    int t = 0;
    for (int i = 1; i <= len; i++) {
        t += a[i] * b;
        a[i] = t % 10;
        t /= 10;
    }
    while (t) {
        a[++len] = t % 10;
        t /= 10;
    }
    //去前导0
    while (len > 1 && !a[len]) len--;
}

int C(int a, int b, int c[]) {
    int len = 1;
    c[1] = 1;
    for (int i = 0; i < cnt; i++) {
        int p = primes[i];
        int s = get(a, p) - get(b, p) - get(a - b, p);
        while (s--) mul(c, p, len);
    }
    return len;
}

void sub(int a[], int b[], int &len) {
    int t = 0;
    for (int i = 1; i <= len; i++) {
        t = a[i] - b[i] - t;
        a[i] = (t + 10) % 10;
        t < 0 ? t = 1 : t = 0;
    }
    while (len > 1 && !a[len]) len--;
}

int main() {
    //加快读入
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);

    get_primes(N - 10);

    int n;
    cin >> n;
    int a1 = C(n + n, n, a);
    int b1 = C(n + n, n - 1, b); // bl下面没有用到，原因是两数相减，我们知道a>b,按着a的长度来就行了

    sub(a, b, a1);

    for (int i = a1; i >= 1; i--) printf("%d", a[i]);
    return 0;
}

4、01序列

给出一个n，要求一个长度为2n的01序列，使得序列的任意前缀中1的个数不少于0的个数,有多少个不同的01序列?

以下为长度为6的序列: 111000 101100 101010 110010 110100

类比一下括号问题，此题就是一个祼的卡特兰数问题。

5、+1 -1序列

n个+1和n个-1构成的2n项 a_1,a_2,···,a_{2n} ，其部分和满足非负性质，即a_1+a_2+···+a_k>=0，(k=1,2,···,2n) ，有多少个不同的此序列?

此典例解析与01序列解析一模一样，即此数列的个数等于第n个Catalan数，此处就不再赘述。

6、凸多边形划分

在一个n边形中，通过不相交于n边形内部的对角线，把n边形拆分为若干个三角形，问有多少种拆分方案？ 如五边形有如下5种拆分方案：

如六边形有如下14种拆分方案：

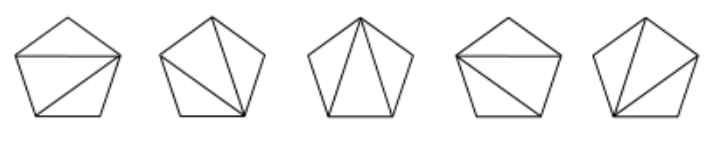
结论：对凸n边形进行不同的三角形分割（只连接顶点对形成n个三角形）数为h[n-2]

这也是非常经典的一道题。我们可以这样来看，选择一个 基边 ，显然这是多边形划分完之后某个三角形的一条边。图中我们假设基边是p_1,p_n，我们就可以用 p_1,p_n 和另外一个点假设为p_i做一个三角形，并将多边形分成三部分(要是i与1,n挨着的话，就是两部分)，除了中间的三角形之外，一边是i边形，另一边是n−i+1边形。i的取值范围是2到n−1。所以本题的解

\large c(n)=c(2)*c(n−1)+c(3)*c(n−2)+...c(n−1)*c(2)

令f(i)=c(i+2)则

\large f(i)=f(0)f(i−1)+f(1)f(i−2)...+f(i−1)f(0)

很明显，这就是一个卡特兰数了。

四、链接资源

五、递推与递归的代码实现

#include <bits/stdc++.h>

using namespace std;
const int N = 10;


int g[N];

// 递归
int f(int n) {
    if (n == 0 || n == 1) return 1;
    int sum = 0;
    // f(0)*f(n-1)+f(1)*f(n-2)+....+f(n-1)*f(0)
    for (int i = 0; i < n; i++)
        sum += f(i) * f(n - 1 - i);
    return sum;
}
int main() {
    // 1、递推法
    g[0] = g[1] = 1;
    for (int i = 2; i < N; i++)
        for (int j = 0; j < i; j++)
            g[i] += g[j] * g[i - j - 1]; // 考虑思路：画括号法

    for (int i = 0; i < N; i++)
        cout << g[i] << endl;

    // 2 、递归法
    for (int i = 0; i < N; i++)
        cout << f(i) << endl;
    return 0;
}