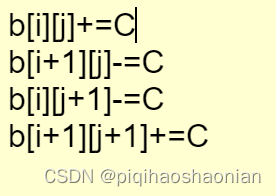python/TangDou/Topic/【前缀和与差分】题单.md

【前缀和与差分】题单

一、公式

前缀和公式

一维：s[i] = a[i] + s[i-1]

二维：s[i][j] = a[i][j] + s[i-1] [j] + s[ i] [j-1] - s[i-1][j-1]

差分公式

一维：b[i] =s[i] - s[i-1]

二维：b[i] = s[i][j] - s[i-1][j]-s[i][j-1]+s[i-1][j-1]

二、题单

P1115 最大子段和

分析 先求每个位置的前缀和，然后去找 该位置前面 前缀和的最小值，如果要求一段和最大，就要用这段和 减去前面最小的值。

一维前缀和解法

#include <bits/stdc++.h>
using namespace std;
const int N = 200100;
int n, a[N], s[N], ans[N];

int main() {
    cin >> n;
    for (int i = 1; i <= n; i++)
        cin >> a[i], s[i] = s[i - 1] + a[i]; // 前缀和

    int mi = 0;
    for (int i = 1; i <= n; i++) {
        ans[i] = s[i] - mi;
        mi = min(mi, s[i]);
    }
    int res = INT_MIN;
    for (int i = 1; i <= n; i++) res = max(res, ans[i]);
    cout << res << endl;
    return 0;
}

DP 解法

状态定义 dp[i]: 走完前i个数字，在此阶段中可以获取到的最大子段和。

状态转移

• 如果从前面的结果中借力划算，那就借力
• 如果借力不合适，那就自己单干

#include <bits/stdc++.h>
using namespace std;
const int N = 200100;
int ans = INT_MIN;
int n;
int a[N], dp[N]; // dp[i]定义：前i个范围内，区间和的最大值

int main() {
    cin >> n;
    for (int i = 1; i <= n; i++) {
        cin >> a[i];
        dp[i] = max(dp[i - 1] + a[i], a[i]);
        ans = max(ans, dp[i]);
    }
    printf("%d\n", ans);
    return 0;
}

P1083 [NOIP2012 提高组] 借教室

暴力

还是先看暴力怎么做吧，对于m次借教室，我们可以每次把区间s\sim t的空教室数r-=d，当有一次r<0时，则当前这个人无法被满足，直接输出-1和当前这个人的号数，然后直接结束程序。如果m次借教室都操作完成后依然没有房间数r<0，则说明所有人都可以被满足，则输出0。

综合上述做法，得分60。

#include <bits/stdc++.h>
using namespace std;
int n, m;
const int N = 1000010;
int r[N];
int main() {
    cin >> n >> m;
    // 每一天可租借教室数
    for (int i = 1; i <= n; i++) cin >> r[i];

    // 从哪天到哪天，借多少个
    for (int i = 1; i <= m; i++) {
        int d, s, t;
        cin >> d >> s >> t;
        // 从开始天到结束天
        for (int j = s; j <= t; j++) {
            r[j] -= d;      // 减去借走的教室数
            if (r[j] < 0) { // 小于0了！
                cout << -1 << endl
                     << i << endl;
                return 0;
            }
        }
    }

    cout << 0 << endl;
    return 0;
}

显然，这样做法的时间复杂度时O(N*M)的，无法通过此题，从而我们可以推知该题正确的时间复杂度应该是log级的。

正解

既然时间复杂度时log级的，于是想到了二分。

再看到每个人借教室的时间可以看成一个区间，且该区间只会对其他在该区间要借教室的人产生影响，对于区间之外的借教室的人是不会产生影响的，于是又想到了差分。

差分序列：（可用于区间增减）记录相邻两个量的变化量，所以当在一段区间[l,r]上增加d时，只需要在l处加d，在r+1处-d 即可。

对于为什么可以二分：如果一个订单无法被满足，则它后面的订单全都不能被满足；如果一个订单可以被满足，则它前面的订单都可以被满足,这恰恰吻合了我们二分的性质。

#include <bits/stdc++.h>
using namespace std;
const int N = 1000010;
#define int long long
#define endl "\n"

int n, m;             // 天数和订单的数量
int r[N];             // 第i天学校有r[i]个教室可借用
int d[N], s[N], t[N]; // 借的教室数目、从第s天借到t天

int b[N];                   // 差分数组
bool check(int mid) {       // 判断能不能通过前mid个订单
    memset(b, 0, sizeof b); // 每次判断都要先初始化差分数组
    int sum = 0;            // 记录需要借的教室数
    // ① 构建差分数组
    for (int i = 1; i <= mid; i++) { // 枚举范围内[1~mid]所有订单
        b[s[i]] += d[i];             // 第i个订单，因为只会对在s~l之间要借用教室的人产生影响，所以可以差分
        b[t[i] + 1] -= d[i];         // 差分,注意:是t[i]+1，因为要包含t[i]这个点
    }
    // ② 还原成原数组,sum=a[i],也就是第i天需要借的教室总数
    for (int i = 1; i <= n; i++) {    // 枚举每一天
        sum += b[i];                  // 因为b是差分数组，所以sum就是在第i天的借教室的总数
        if (sum > r[i]) return false; // 如果要借的教室多于空的教室,返回不可行
    }
    return true; // 返回可行
}
signed main() {
    cin >> n >> m;                                            // n:天数，m：订单数量
    for (int i = 1; i <= n; i++) cin >> r[i];                 // 第i天可以租借的教室数量
    for (int i = 1; i <= m; i++) cin >> d[i] >> s[i] >> t[i]; // 借多少个，从哪天借到哪天

    /*
    ① 整体检查，如果所有订单都能通过，则输出0
      先定性，再定量！
      我们先不思考二分不二分，先用check函数获取所有订单是不是可以通过，如果能通过，那二分个啥！
      如果不能过，再已知有问题订单的情况下，再去找出问题订单，这样思路是最清晰的！
      避免不管是否有问题订单，全都冗杂到一个二分检查办法中去，那样容易思路不清，造成丢分！
    */
    if (check(m)) {        // 如果全部满足
        cout << 0 << endl; // 输出0
        exit(0);           // 直接结束程序
    }
    /*
    ② 整体检查未通过，知道肯定有订单无法满足，此时，再想办法找出是哪个订单第一个出现不满足的情况
    难道要一个个订单检查吗？
    不断的增加订单，会使得差分数组变化，但我们只看差分数组是不能判断是否有问题发生的，需要把差分数组还原
    为原数组后，才能进行检查,每输入一个订单，就还原一下原数组，那样就太慢了。
    能不能少还原，还能判断准呢？
    答：可以的，因为这件事具有单调性！第x个订单加上后:
    (1)如果1~x都符合条件，那证明前面的x-1个订单都是OK的，
    (2)如果1~x不符合条件，那后续的追加更多订单后的检查也肯定会失败！
    所以，可以使用二分进行求解查找是哪个订单导致第一个失败情况出现。
    */
    int l = 1, r = m; // 二分左右区间
    while (l < r) {
        int mid = l + r >> 1;
        if (check(mid))  // 如果可行
            l = mid + 1; // 增多订单
        else             // 否则
            r = mid;     // 减少订单
    }

    if (l == r) cout << 0 << end;
    ;

    cout << "-1" << endl
         << l; // 输出-1和 第一个不符合条件的订单
}

P3406 海底高铁

题意

每一个条铁路都会被经过多次，求这一条铁路是办卡+充值花的钱少,还是直接买多次票花的钱少。

分析 我们其实只需要知道一条铁路被访问了几次就可以了，再通过比较 c+b*n 和 a 的值，就可以知道是买票好还是买卡好了。

一个点到另外一个点的路径中，中间经过的铁路都会被访问一遍，如果每次都一个一个的加这样太慢了,会TLE

发现这些铁路实质上是一维的，并且是关于区间的修改的,那么就可以用差分优化了

#include <bits/stdc++.h>
using namespace std;
const int N = 100005;
#define int long long // 数据范围是10^5*10^5,所以注意要开ll
#define endl "\n"
int p[N];             // 要访问的城市顺序
int x[N], y[N], z[N]; // 买票,充值,买卡
int b[N];             // 差分数组
int res;              // 结果
int n, m;             // 共n个城市，要去m个城市

signed main() {
    cin >> n >> m;                                           // 共n个城市，要去m个城市
    for (int i = 0; i < m; i++) cin >> p[i];                 // 访问顺序,下标都是从0开始的
    for (int i = 1; i < n; i++) cin >> x[i] >> y[i] >> z[i]; // 每个城市的买票、充值、买卡价格，此处下标从1开始，是因为P0不需要再到P0

    for (int i = 1; i < m; i++) {   // 0号点是出发点，没有意义，不讨论，从1号开始，最大是 m-1
        int s = p[i - 1], t = p[i]; // 起点, 终点
        if (s > t) swap(s, t);      // 我KAO，原来题意是说：如果你从2~5去则一定走了2,3,4,5这四个城市，铁路按线段处理，即2,3,4号线段
        b[s] += 1, b[t] -= 1;       // s在内，t不在内，因为是按线段处理的
    }

    for (int i = 1; i <= n; i++) b[i] += b[i - 1]; // 差分数组变形为前缀和数组

    // 判断一下 n*a[i]和n*b[i]+c[i]的大小
    for (int i = 1; i < n; i++)
        res += min(b[i] * x[i], b[i] * y[i] + z[i]);
    // b[i]:走几次，x[i]*b[i]:买票需要花费多少钱；b[i] * y[i] + z[i]:办卡+冲值共需要花费多少钱
    // 两个打擂台，谁少就用谁，每一块线段都花费最少，整体必须花费最少，贪心
    cout << res << endl; // 输出
}

P5638 光骓者的荣耀

题目大意 用最少时间要将所有城市全部访问完，若有传送器可使用传送器。

坑点

• 需要考虑传送器数量与城市的数量 ，若传送器大于城市输出0
• 需要考虑数据范围较大，long long int

数据范围 开一个大于10的6次方的数据

思路

上图是一个n = 6的样例。从城市1到城市6，需要3+2+4+5+4=18天。

假如传送器的半径为2。可以逐个枚举。

• 如果在城市1使用传送器，则一下子可到达城市3，然后城市3到城市6，需要13天。这种情况下从城市1到城市6，需要13天。

• 如果在城市2使用传送器，则从城市1先用3天的时间到达城市2，再用传送器到达城市4，从城市4到城市6需要9天。这种情况下从城市1到城市6，共需要3 + 9 = 12天。

• 如果在城市3使用传送器，则从城市1到城市3需要5天，从城市3使用传送器一下子到达城市5，从城市5到城市6需要4天。这种情况下从城市1到城市6，共需要5+4=9天。

• 如果在城市4使用传送器，则从城市1到城市4需要9天，从城市4使用传送器一下子到达城市6。这种情况下从城市1到城市6，共需要9天。

• 如果在城市5使用传送器，则从城市1到城市5需要14天，从城市5使用传送器一下子到达城市6。这种情况下从城市1到城市6，共需要14天。

所以在城市3或城市4使用传送器，可以使得总共花费的时间最少。

Code

#include <bits/stdc++.h>
using namespace std;
#define int long long
#define endl "\n"
const int N = 1000010;
int n, k;
int a[N], s[N];
int ans = LONG_LONG_MAX; // 预求最小先设最大

signed main() {
    cin >> n >> k;
    for (int i = 2; i <= n; i++) { // i代表第i个城市
        cin >> a[i];               // a[i]代表第i-1个城市到第i个城市需要的时间
        s[i] = s[i - 1] + a[i];    // 利用前缀存储从第1个城市到第i+1个城市的累积时间
    }
    // 感悟：代码越多，可读性越强
    for (int i = 1; i <= n; i++) {       // 遍历每个城市
        int far = i + k;                 // 传送到最远的点
        if (far >= n) far = n;           // 最远不能超过n点
        int time = s[i] + s[n] - s[far]; // s[n]-s[far]= 剩余道路需要走的时间,s[i]:前面道路需要走的时间
        ans = min(ans, time);            // 取最小值
    }
    cout << ans << endl; // 输出
}

P1719 最大加权矩阵

O(N^4)算法

#include <bits/stdc++.h>
using namespace std;
const int N = 130;
int n;
int a[N][N]; // 存储题目中的矩阵
int s[N][N]; // 二维前缀和

int main() {
    cin >> n;
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= n; j++) {
            cin >> a[i][j];
            s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + a[i][j];
        }
    }

    int mx = INT_MIN; // 存储答案
    // 遍历左上角坐标，与，右下角坐标
    for (int x1 = 1; x1 <= n; x1++) {
        for (int y1 = 1; y1 <= n; y1++) {
            for (int x2 = 1; x2 <= n; x2++)
                for (int y2 = 1; y2 <= n; y2++) {
                    if (x2 < x1 || y2 < y1) continue;                                            // 如果左上角比右下角还要大，就不用求了，下一个
                    mx = max(mx, s[x2][y2] + s[x1 - 1][y1 - 1] - s[x2][y1 - 1] - s[x1 - 1][y2]); // 求最大值
                }
        }
    }
    cout << mx << endl; // 输出
    return 0;
}

O(N^3)算法【选读】

引子 给出一段序列，选出其中连续且非空的一段使得这段和最大。
第一行是一个正整数N，表示了序列的长度。(N<=200000)

这是 P1115 最大子段和 的描述，也就是本题的一维版本。

DP方程：dp[i]=max(dp[i-1]+a[i],a[i]) a[i]表示这个数列的第i项。

那么我们如何来处理这一题呢？

我们可以考虑将矩形压缩成一维，比如处理一个2行的矩形时，将a [i][j]与a[i-1][j]相加，成为一个新的数组f[n]，再使用上述代码进行动态规划，找出局部最优解。

那如何来快速将矩形折叠呢？

我们可以选择 前缀和

简单来说，就是在输入的时候，再次加上a[i-1][j]，这样可以用减法来快速表示压缩的矩形。

具体代码如下：

cin >> n;
for(int i=1;i<=n;++i)
    for(int j=1;j<=n;++j){
        cin >> a[i][j];
        a[i][j]+=a[i-1][j];//根据前缀和定义处理
    }

用样例来表示，输入的是：

0   -2  -7   0
9    2  -6   2
-4   1  -4   1 
-1   8   0  -2

在经过前缀和处理之后，输出的是这个：

0   -2  -7    0
9    0  -13   2
5    1  -17   3
4    9  -17   1

可以模拟一下，a[i][j] - a[i-k][j]正好是以i为最下面一行，往上k行的压缩结果，这就很方便地表示了压缩后的矩形。

那又怎么循环找出各行为最下一行，不同行数的矩阵最大值呢？ 我用i表示以i为最下一行，k表示向上k行，代码如下:

  for(i=1;i<=n;i++){
    for(k=1;k<=i;k++){

    }
 }

k<=i，保证了i-k>=0。

那再次循环，运用第一个代码的简单变形，可以求出以i为最下一行，向上k行的矩形最大值，多次更新ans，愉快AC。

Code

#include <bits/stdc++.h>
using namespace std;
const int N = 150;
int a[N][N];

int main() {
    int n;
    cin >> n;
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= n; j++) {
            cin >> a[i][j];
            a[i][j] += a[i - 1][j]; // 按列计算前缀和
        }

    int ans = INT_MIN;                         // 预求最大，先设最小
    for (int i = 1; i <= n; i++)               // 最底下一行
        for (int k = 1; k <= i; k++) {         // 往上k行
            int dp[N] = {0};                   // dp[j]表示压缩的矩形前j列的最大累加值
            for (int j = 1; j <= n; j++) {     // 第j列
                int s = a[i][j] - a[i - k][j]; // 求压缩的矩形第j列的值
                dp[j] = max(dp[j - 1] + s, s); // 动态规划,到j列为止，最大的连续累加和
                ans = max(ans, dp[j]);         // 更新答案
            }
        }
    cout << ans << endl; // 愉快AC
    return 0;
}

P2004 领地选择

二维前缀和祼题，不解释。

#include <bits/stdc++.h>
using namespace std;
const int N = 1010;
int n, m, c;
int a[N][N], s[N][N];
int mx = INT_MIN;

int main() {
    cin >> n >> m >> c;
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= m; j++) {
            cin >> a[i][j];
            s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + a[i][j]; // 构建二维前缀和
        }

    int x, y;
    for (int i = c; i <= n; i++) // 边长为c
        for (int j = c; j <= m; j++) {
            if (s[i][j] - s[i - c][j] - s[i][j - c] + s[i - c][j - c] > mx) {
                mx = s[i][j] + s[i - c][j - c] - s[i - c][j] - s[i][j - c];
                x = i - c + 1;
                y = j - c + 1;
            }
        }
    printf("%d %d", x, y);
    return 0;
}

P3397 地毯

分析 看到这里的时候，我就想到了一个矩阵的某个子矩阵进行加减，瞬间想到二维差分和二位前缀和,二位差分的公式为：

由差分算的二位前缀和公式：

#include <bits/stdc++.h>
using namespace std;

const int N = 1010;
int b[N][N], s[N][N];
int n, m;

int main() {
    cin >> n >> m;
    while (m--) {
        // 从0开始构建差分数组
        int x1, y1, x2, y2;
        cin >> x1 >> y1 >> x2 >> y2;
        b[x1][y1] += 1; // 进行子矩阵的加减，差分
        b[x2 + 1][y1] -= 1;
        b[x1][y2 + 1] -= 1;
        b[x2 + 1][y2 + 1] += 1;
    }
    // 还原为原始数组
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= n; j++) {
            s[i][j] = b[i][j] + s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1]; // 把之前的加减结果进行求和
            printf("%d ", s[i][j]);                                          // 注意输出格式，每个数带一个空格
        }
        printf("\n"); // 结束一行的输出输出一个换行符号
    }
    return 0;
}