4.3 KiB
一、题目描述
地图上有 N 个目标,用整数 X_i,Y_i 表示目标在地图上的位置,每个目标都有一个价值 W_i。
注意:不同目标可能在同一位置。
现在有一种新型的激光炸弹,可以摧毁一个包含 R×R 个位置的正方形内的所有目标。
激光炸弹的投放是通过卫星定位的,但其有一个缺点,就是其爆炸范围,即那个正方形的边必须和 x,y 轴平行。
求一颗炸弹 最多 能炸掉地图上 总价值为多少 的目标。
输入格式
第一行输入正整数 N 和 R,分别代表地图上的目标数目和正方形包含的横纵位置数量,数据用空格隔开。
接下来 N 行,每行输入一组数据,每组数据包括三个整数 X_i,Y_i,W_i,分别代表目标的 x 坐标,y 坐标和价值,数据用空格隔开。
输出格式 输出一个正整数,代表一颗炸弹最多能炸掉地图上目标的总价值数目。
数据范围
0≤R≤10^9
0<N≤10000
0≤X_i,Y_i≤5000
0≤W_i≤1000
输入样例:
2 1
0 0 1
1 1 1
输出样例:
1
二、解题思路
二维前缀和问题
1、二维前缀和要注意空间受限
- ① 想使用二维前缀和,需要先看一下数据范围:
0<=X_i,Y_i<=5000对于二维数组而言,每维开到5000可不是一个小数字,要小心!
因为数组是5000 \times 5000,占用空间 5000 \times 5000 \times 4bytes=5000 \times 5000 \times 4/1024/1024MB=95MB
回头看一下内存的上限范围:168MB,也就是开一个5000 \times 5000的数组没有问题,但是不能开两个,开两个将MLE!
不能开两个是啥意思?为啥要思考两个的问题?
因为我们对于前缀和,一般喜欢用一个原始数组a[N][N],再开一个前缀和数组s[N][N],这样按传统就是两个数组啦~,现在看来只能开一个,也就是不保存原始数组,直接在原始数组上加和得到前缀和数组。
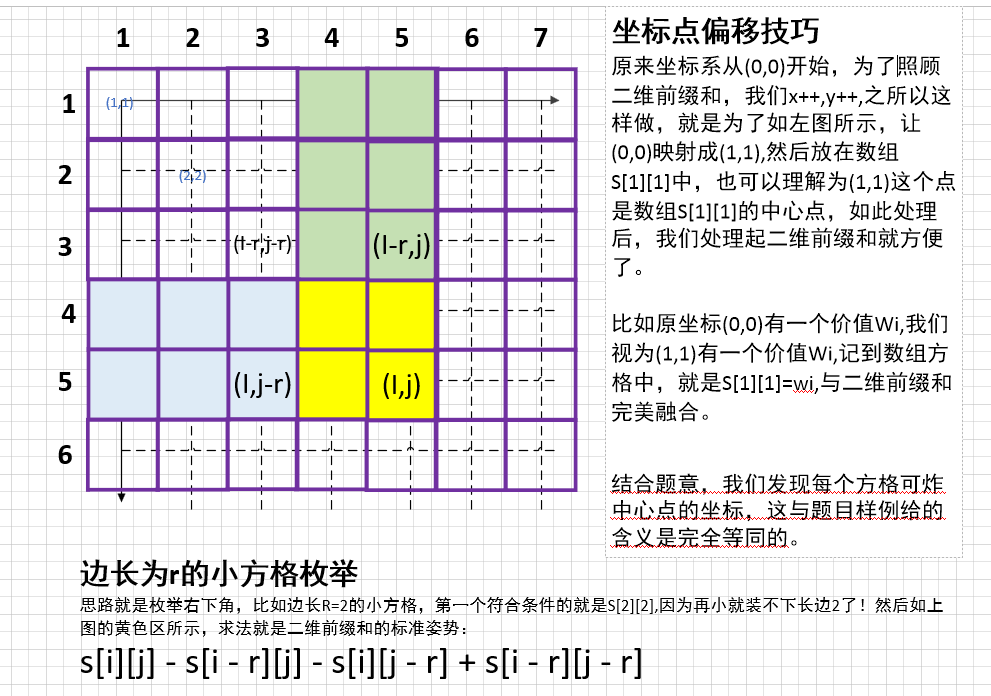
2、前缀和要注意下标从1开始
x,y坐标是从0开始的,我们一般的一维前缀和、二维前缀和,下标是从1开始的, 需要做一下坐标的+1变换
3、二维前缀和要注意点与格子的区别,加0.5进行偏移
先用测试用例模拟一下,你就会明白,原来这个炸弹的方框,不是说刮着边就能把某个坐标炸掉,而且必须 包着 某个坐标才行!
解决办法:整体偏移0.5
4、注意数据范围
炸弹的范围会超过5000,而且如果是范围是0直接返回0
四、实现代码
#include <bits/stdc++.h>
using namespace std;
const int N = 5010, M = 5001;
// 前缀和数组
int s[N][N];
int main() {
// n:点的数量,R:边长
int n, R;
cin >> n >> R;
// 这里本题数据有些坑,R有时输入会比我们整个矩阵大,所以这里设置输入的R过大,就直接取M
R = min(R, M); // R太大,对于我们来说没有意义,因为它>5001时,就把所有位置全部摧毁掉~
for (int i = 1; i <= n; i++) {
int x, y, w;
cin >> x >> y >> w;
// 因为每题的(x,y)是默认下标从0开始,与前缀和的习惯不太相符,所以,这里直接将原坐标x+1,y+1,映射到下标从(1,1)开始
x++, y++; // 0≤Xi,Yi≤5000
s[x][y] += w; // 不同目标可能在同一位置,s数组同时也充当了a数组
}
// 二维前缀和公式
for (int i = 1; i <= M; i++)
for (int j = 1; j <= M; j++)
s[i][j] += s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1];
// 枚举所有边长为R的正方形,取最大值就OK了(枚举的是右下角) => (R-1)*(R-1)的矩阵
int res = 0;
for (int i = R; i <= M; i++)
for (int j = R; j <= M; j++) // 二维前缀和应用
res = max(res, s[i][j] - s[i - R][j] - s[i][j - R] + s[i - R][j - R]);
// 输出结果
printf("%d\n", res);
return 0;
}