python/TangDou/AcWing_TiGao/T6/PaiXu/106.md

##AcWing 106. 动态中位数

一、题目描述

依次读入一个整数序列，每当已经读入的整数个数为奇数时，输出 已读入的整数 构成的序列的 中位数。

输入格式 第一行输入一个整数 P，代表后面数据集的个数，接下来若干行输入各个数据集。

每个数据集的第一行首先输入一个代表数据集的编号的整数。

然后输入一个整数 M，代表数据集中包含数据的个数，M 一定为奇数，数据之间用空格隔开。

数据集的剩余行由数据集的数据构成，每行包含 10 个数据，最后一行数据量可能少于 10 个，数据之间用空格隔开。

输出格式 对于每个数据集，第一行输出两个整数，分别代表数据集的编号以及输出中位数的个数（应为数据个数加一的二分之一），数据之间用空格隔开。

数据集的剩余行由输出的中位数构成，每行包含 10 个数据，最后一行数据量可能少于 10 个，数据之间用空格隔开。

输出中不应该存在空行。

数据范围 1≤P≤1000,1≤M≤99999, 所有 M 相加之和不超过 5×10^5。

输入样例：

3 
1 9 
1 2 3 4 5 6 7 8 9 
2 9 
9 8 7 6 5 4 3 2 1 
3 23 
23 41 13 22 -3 24 -31 -11 -8 -7 
3 5 103 211 -311 -45 -67 -73 -81 -99 
-33 24 56

输出样例：

1 5
1 2 3 4 5
2 5
9 8 7 6 5
3 12
23 23 22 22 13 3 5 5 3 -3 
-7 -3

二、算法分析

由于是只关心中位数，而且是一个动态不停求中位数的过程，这有一个经典的作法：对顶堆

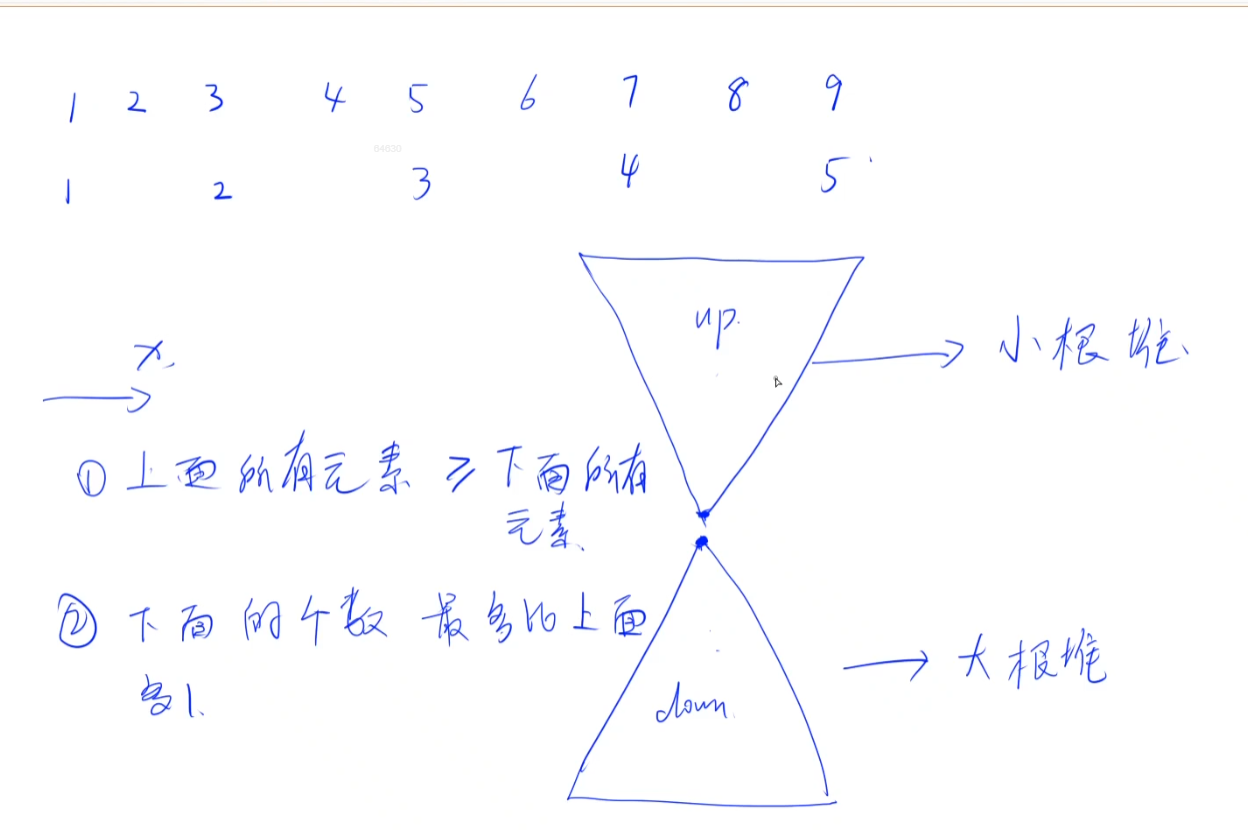
• 1、 开两个堆，一个是大根堆，一个是小根堆，小根堆在上，大根堆在下 小于中位数的都放在大根堆(下面的堆)，大于中位数的都放在小根堆(上面的堆) 此时，两个堆挨着的位置就是中位数。 这两个堆满足了两个性质：
  • ① 上面的所有元素都大于等于下面的所有元素
  • ② 下面的个数最多比上面多1个

注意:两个堆其实是没有交集的，要注意！

• 2、假设最初时我们的两个堆都已经维护好了，现在新来了一个数字x,我们把它与中位数进行比较，如果大于中位数，就放到上面去，否则就放到下面去。这样操作，我们就满足了 ① 操作。但 ②怎么来满足呢？这个也简单，就是判断一下现在操作的堆中元素数量与另一个堆的数量，是不是不再满足最多多一个，如果是的话，就把 堆顶 的那个元素弹出，并且加入到另一端去。

思考：为什么是堆顶的呢？因为只有堆顶的才是两者的分界线啊。

三、实现代码

#include <bits/stdc++.h>
using namespace std;

int T;
int main() {
    // 加快读入
    ios::sync_with_stdio(false), cin.tie(0);
    cin >> T;

    while (T--) {
        int n, m;
        cin >> m >> n;
        // 对于每个数据集，第一行输出两个整数，分别代表数据集的编号以及
        // 输出中位数的个数（应为数据个数加一的二分之一），数据之间用空格隔开。
        printf("%d %d\n", m, (n + 1) / 2);

        priority_queue<int, vector<int>, greater<int>> up; // 小顶堆
        priority_queue<int> down;                          // 默认大顶堆

        // 对顶堆
        int cnt = 0;
        for (int i = 1; i <= n; i++) {
            int x;
            cin >> x;

            if (!up.size() || x >= up.top())
                up.push(x);
            else
                down.push(x);

            if (up.size() > down.size() + 1) down.push(up.top()), up.pop();
            if (down.size() > up.size()) up.push(down.top()), down.pop();

            // 奇数才输出
            if (i & 1) {
                printf("%d ", up.top());
                if (++cnt % 10 == 0) puts(""); // 题目要求十个一换行
            }
        }
        // 最后不足10个，也需要输出一个的换行
        if (cnt % 10) puts("");
    }
    return 0;
}