4.8 KiB
一、题目描述
城市的规划在城市建设中是个大问题。
不幸的是,很多城市在开始建设的时候并没有很好的规划,城市规模扩大之后规划不合理的问题就开始显现。
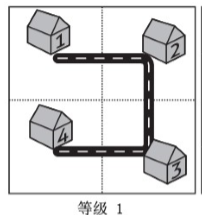
而这座名为 Fractal 的城市设想了这样的一个规划方案,如下图所示:
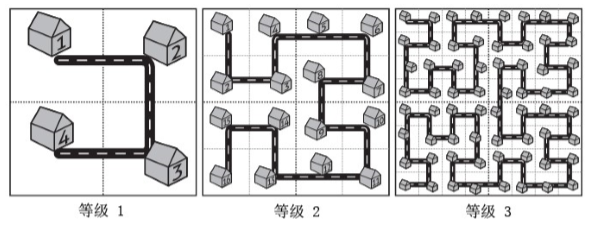
当城区规模扩大之后,Fractal 的解决方案是把和原来城区结构一样的区域按照图中的方式建设在城市周围,提升城市的等级。
对于任意等级的城市,我们把正方形街区从左上角开始按照道路标号。
虽然这个方案很烂,Fractal 规划部门的人员还是想知道,如果城市发展到了等级 N,编号为 A 和 B 的两个街区的 直线距离 是多少。
街区的距离指的是街区的 中心点之间的距离,每个街区都是边长为 10 米的正方形。
输入格式
第一行输入正整数 n,表示测试数据的数目。
以下 n 行,输入 n 组测试数据,每组一行。
每组数据包括三个整数 N,A,B,表示城市等级以及两个街区的编号,整数之间用空格隔开。
输出格式
一共输出 n 行数据,每行对应一组测试数据的输出结果,结果四舍五入到整数。
数据范围
1≤N≤31,1≤A,B≤2^{2N},1≤n≤1000
输入样例:
3
1 1 2
2 16 1
3 4 33
输出样例:
10
30
50
二、解题思路
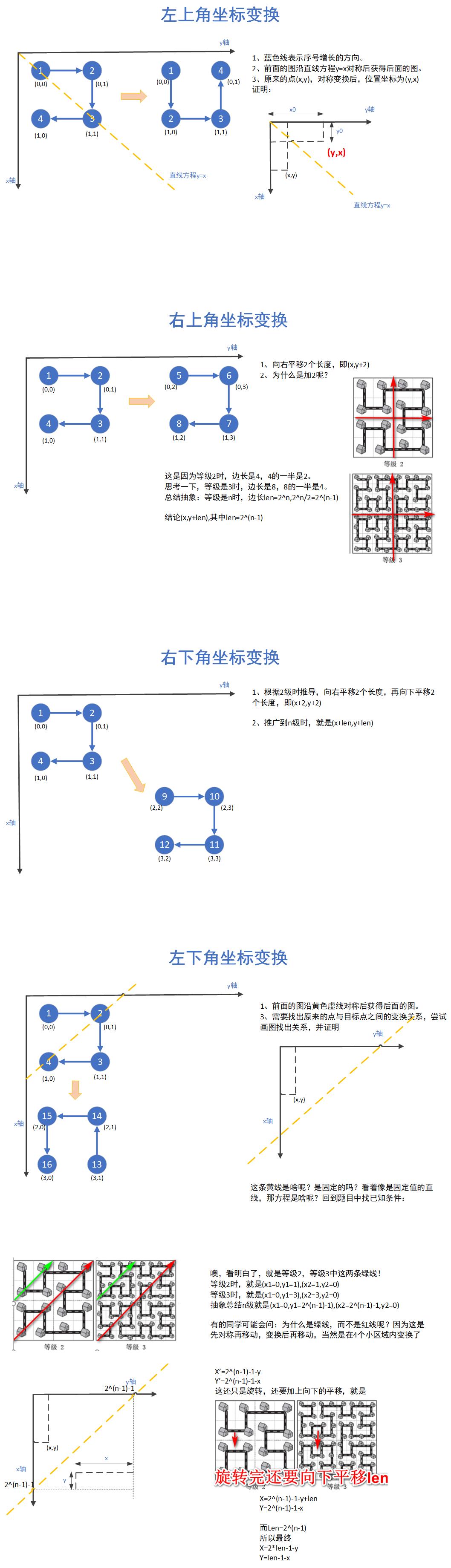
我们假设想求9号点的坐标,当然,我们可以用眼睛看~,但是如果层级太多,眼睛看着太累,而且,计算也不会用眼睛看,我们给它一个办法:
是这样思考问题的:
9号坐标我是不知道的,但是,我们知道,9号在自己的小区间,也就是4方格子中,它是最小的,而且,等级2是由等级1变换而来,1这个数字,它经过一顿坐标变换,可以到达9, 如果我们知道了1的坐标(x,y),再同样经过那些坐标变换过程,是不是就能求出9的坐标了?所以,这是一个大问题向小问题转化的过程,也就是N级的问题,我们可以先求N-1级的原来对应点的坐标,再通过对应点的坐标经过同样的变换,就得到了现在的坐标。
那9的原来坐标点是1,10的原来坐标点是2,11的原来坐标点是3,12的原来坐标点是4,噢,似乎是与数字4有取模的关系!既然要取模,那么最好下标从0开始,所以,我们不再说1\sim 16,改成0 \sim 15吧!
那就是8:0,9:1,10:2,11:3,也就是8\%4=0,8\%4=1,10\%4=2,11\%4=3
等一下,这个4是啥东西?常量吗?应该不是,似乎是等级2中整体数字数量4^2/4=4
推广到n级,就是block=4^n/4=2^{2n-2}
下面就是如何进行坐标变换了:
Code
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
struct Point {
LL x, y;
};
// 功能:在一个n级的矩阵中,求标号为a的格子坐标
Point get(LL n, LL a) {
if (n == 0) return {0, 0}; // 1级是4个,2级是16个,3级是64个,0级时只有一个点,坐标就是(0,0)
LL block = 1ll << n * 2 - 2; // 1个块的大小:1级1个,2级4个,3级16个,也就是4^(n-1)=2^(2n-2)
LL len = 1ll << n - 1; // 1级移动1,2级移动2,3级移动4,总结:n级2^(n-1)
auto p = get(n - 1, a % block); // n-1级时,a这个点的原来对应格子在坐标是什么
LL x = p.x, y = p.y;
int z = a / block; // 0~3哪个块
if (z == 0) return {y, x}; // y=x对称
if (z == 1) return {x, y + len}; // 向右平移len个距离
if (z == 2) return {x + len, y + len}; // 向右平移len个距离,再向下移动len个距离
if (z == 3) return {len * 2 - 1 - y, len - 1 - x}; // 关于2^(n-1)-1那条直线对称
}
int main() {
int T;
scanf("%d", &T);
while (T--) {
LL n, a, b;
scanf("%lld%lld%lld", &n, &a, &b);
auto pa = get(n, a - 1); // 下标从0开始,方便取模
auto pb = get(n, b - 1);
double dx = pa.x - pb.x, dy = pa.y - pb.y;
printf("%.0lf\n", sqrt(dx * dx + dy * dy) * 10);
}
return 0;
}